Maxwell's equations

Properties if the electric and magnetic fields as predicted by Maxwell's equations

Classical physics is our model of the laws that govern the behavior and interactions of macroscopic objects in the world around us.  All the laws of classical physics were known by the end of the 19th century.  Classical physics works well describing and predicting almost all everyday phenomena, but it starts to fail when things get too ... .  (You can insert any extremes here, for example big, small, hot, cold, fast, etc.)

In classical physics the world is made of matter particles that behave according to Newton's laws of motion.  To use Newton's laws, we need to know which forces are acting on the particles.  The interactions that give rise to the forces between the particles are represented by fields.  Electric and magnetic fields represent the electromagnetic interactions.  If we know the fields, we know the electric and the magnetic forces acting on charged particles.

F = Felectric +  Fmagnetic  = qE + qv × B = q(E + v × B).

In classical physics our model for the electromagnetic fields is a set of four equations, called Maxwell's equations.  They let us predict E and B.  They have a broader range of applicability than Newton's laws.  They are relativistically correct, and correctly describe the fields when relative speeds approach the speed of light.  But the classical model for the electromagnetic fields no longer describes observations correctly on the scale of atoms or elementary particles.

Static fields

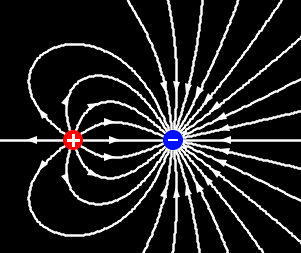imageMaxwell's equations predict that static electric fields, i.e. field that do not change with time, are produced by charges.  Charges are sources and sinks of field lines.  Static electric field lines begin on positive and end on negative charges. 
Static electric field lines NEVER form loops. 

The static electric field is a conservative field.  If you do work on a charge against the static electric field, this work is stored as potential energy.  The potential energy is a function of position only.  You can let the electric field do work to recover the energy you expended in moving the charge.

In statics, Maxwell's equations for the electric field combine to give you Coulomb's law and the principle of superposition.  Everything else is just vector addition.

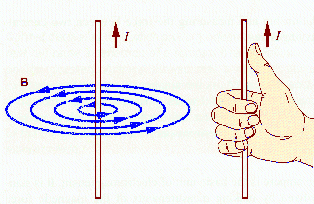imageMaxwell's equations predict that static magnetic fields are produced by steady currents.  There are no magnetic charges, and therefore no sources and sinks for magnetic field lines. 

Static magnetic fields lines ALWAYS form closed loops. 
They encircle moving charges according to the right hand rule.

Induced fields

imageIf we do NOT restrict ourselves to steady state conditions, two additional terms appear in Maxwell's equations.

(1) ∮A E∙dA = Qinside/ε0
(2) ∮Γ E∙ds = -∂/∂t∫AB·dA
(3) ∮A B∙dA = 0
(4) ∮Γ B∙ds =  μ0Ithrough Γ  + (1/c2)∂/∂t∫AE·dA

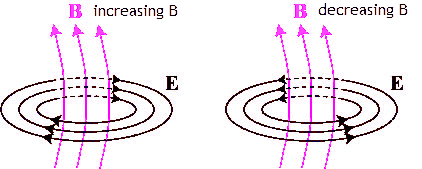
Maxwell's equations tell us that there is another source of electric and magnetic fields, when either of those fields changes with time.

The key word is CHANGE.  The fields produced by this CHANGE are called dynamic or induced fields.  The induced fields do not have sources or sinks. 
Field lines of induced, dynamic fields ALWAYS form closed loops.  They always have circulation.

Mathematical definition of circulation of a vector field:
Take any closed loop, for example a circle.  At a fixed time, move in small steps ∆r once around the loop.  (You should take infinitessimally small steps.)  At each step calculate the product of the tangential component of the field time ∆r.  For the electric field, for example, calculate E∙∆r.  Sum up all these products as you go once around the loop.

Example

The circulation of E around a closed loop = lim∆r-->0Σaround loop E∙∆r = ∫around loopE·dr.

For induced fields, the circulation is always non-zero.

How much circulation is there?

Maxwell's equations tell us about the magnitude and the direction of the circulation.  One of the equations is called Faraday's law.  For the absolute value or magnitude, Faraday's law states that the circulation of the electric field E around any closed loop is equal to the rate of change of the magnetic flux through the area enclosed by the loop.

Remember flux:

The flux of a vector field through a surface area is the amount of whatever the field represents passing through the area.  The total flux depends on strength of the field, the size of the surface area it passes through, and on how the area is oriented with respect to the field.

We have defined the electric flux as dΦE = E dA cosθ,  ΦE = ∫AE·dA.
The magnetic flux is defined in an analogous way as dΦB = B dA cosθ,  ΦB = ∫AB·dA.

Another of Maxwell's equations is the Ampere-Maxwell law.  It states that the circulation of the magnetic field B around any closed loop is the sum of two terms.  The static term is proportional to the current flowing through the loop and the dynamic term is proportional to the rate of change of the electric flux through the area enclosed by the loop.

This interplay between induced electric and magnetic fields leads to the production of electromagnetic wave.
Electromagnetic waves are solutions to Maxwell's equations, even in free space, when no charges or currents are present.

Problem:

Find the magnetic flux through each of the coils below.

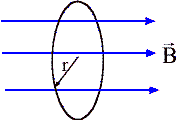image(a)  A magnetic field of magnitude B = 5 mT points along the normal of a circular turn of wire of radius r = 1 cm.

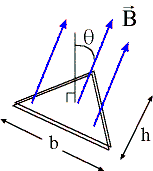image(b)  A magnetic field of magnitude B = 5 mT makes an angle θ = 20o with the normal of triangular coil of 50 turns with base b = 5.0 cm and height h = 4 cm.

Solution:

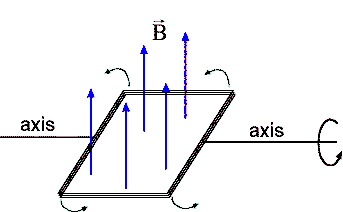imageProblem:

A rectangular loop of N turns is rotating about an axis in a region of uniform magnetic field, as shown in the figure on the right.
Describe how the magnetic flux through the loop is changing with time.

Solution: