In classical physics, we can classify optical phenomena into one of two categories: ray optics and wave optics.
Light is a transverse electromagnetic wave. In many situations, the wavelengths of the light being studied are very small
compared to the dimensions of the equipment used to study the light. Under these conditions we can make an approximation called
geometrical optics or ray optics. Consider the wavelength scale of light waves.
Wavelengths in the middle of the visible band are on the order of 500 nm.
So a laser beam with a diameter of 1 mm has a diameter of 2000 wavelengths.
Individual atoms in a solid are separated by distance on the order of 0.1 nm.
So, as far as visible light is concerned, matter is quasi-continuous.
If the wavelengths of the light become comparable to the dimensions of the
equipment, then we study optical phenomena using the classical theory of radiation, or wave optics.
Wave optics contains all of ray optics, but the
mathematical treatment is much more involved.
Diffraction and interference are phenomena observed with all waves.
Diffraction can only be observed with waves traveling in two or three
dimensions. (We already encountered interference when studying
mechanical waves
on a string and
sound waves in physics 2135.)
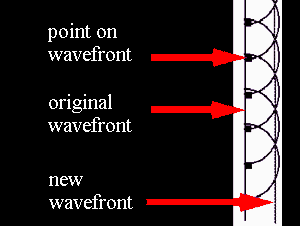Diffraction is the tendency of a wave emitted from a finite source or
passing through a finite aperture to spread out as it propagates. Diffraction results from the interference of an infinite number of waves
emitted by a continuous distribution of source points in two or three dimensions.
Huygens' principle
lets us treat wave propagation by considering every point on a wave front to be a secondary source of
spherical wavelets. These wavelets propagate outward with the characteristic
speed of the wave. The wavelets emitted by all points on the wave front
interfere
with each other to produce the traveling wave. Huygens' principle also holds
for electromagnetic waves. When studying the propagation of light, we can
replace any wave front by a collection of sources distributed uniformly over the
wave front, radiating in phase.
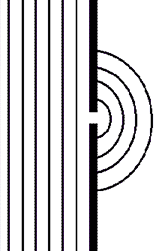When light passes through a small opening, comparable in size to the
wavelength λ of the light, in an otherwise opaque obstacle, the wave front on
the other side of the opening resembles the wave front shown on the right.
The light spreads around the edges of the obstacle. This is the phenomenon of
diffraction. Diffraction
is a wave phenomenon and is also observed with water waves in a ripple tank.
Water waves in a ripple tank
| A single large slit |
A single small slit |
 |
 |
Please watch: Apertures
and Diffraction - Exploring Wave Motion (YouTube)
The single slit
When light passes through a single slit whose width w is on the order of the wavelength of the light, then we can observe a single slit diffraction pattern on a
screen that is a distance L >> w away from the slit. The intensity is a function of angle. Huygens' principle tells us that each part of the slit can be thought of as an
emitter of waves. All these waves interfere to produce the diffraction pattern. Where crest meets crest we have constructive interference and
where crest meets trough we have destructive interference.
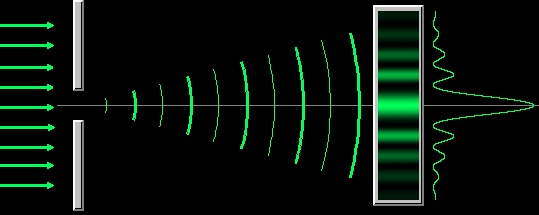
Very far from a point source the wave fronts are essentially plane
waves. This is called the Fraunhofer regime, and the diffraction pattern is called Fraunhofer diffraction. The positions of all
maxima (constructive interference) and minima (destructive interference) in the
Fraunhofer diffraction pattern can be calculated fairly easily.
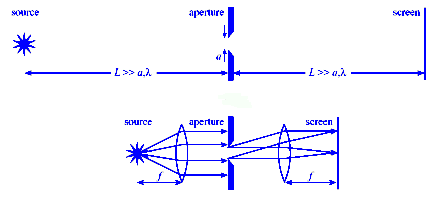
The Fraunhofer approximation, however, is only valid when the source, aperture, and detector are all very far apart or
when lenses are used to convert spherical waves into plane waves. Being
very far apart means that the distances between source, aperture, and detector
must be much greater than the width of the aperture.
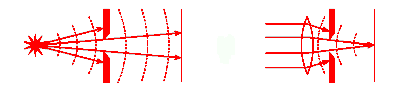The
Fresnel regime is the near-field regime. In this regime the wave
fronts are curved, and their mathematical description is more involved.
The positions of all maxima and minima in the Fraunhofer diffraction pattern from a single slit can be found
from the following simple arguments.
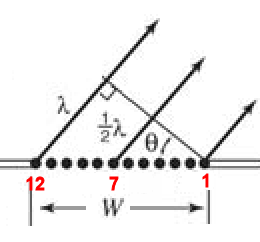Consider a slit of width w, as shown in the
diagram on the right. A plane wave is incident from the bottom and all points oscillate in phase inside the slit.- For light leaving the slit in a particular direction defined by the angle θ, we may have destructive
interference between the ray at the right edge (ray 1) and the middle ray (ray 7).
To arrive at a distant screen perpendicular to the direction of
propagation of the rays, the rays coming from different points
inside the slit have to travel different distances. They have
a different optical path length. If ray 7
has to travel an extra distance of one-half wavelength (λ/2)
compared to ray 1, then ray 1 and ray 7 destructively interfere. Crest meets trough.
- The optical path length (OPL) of a
light ray traveling from point A to point B is defined as c times
the time it takes the ray to travel from A to B. In free space
the optical path length is just the distance d between the points.
In a transparent medium with index of refraction n, it equals n
times this distance, OPL = nd, because the light moves with speed c/n.
If the optical path length of two rays differs by λ/2,
the two rays interfere destructively. For ray 1 and ray 7 to be half a wavelength
out of phase we need
(w/2)sinθ = λ/2 or w sinθ = λ.
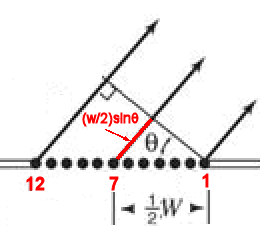But from geometry, if these two rays interfere destructively, so do rays 2 and
8, 3 and 8, and 6
and 10, 5 and 11, and 6 and 12.
In effect, light from one half of the opening interferes destructively
and cancels out light from the other half.
Destructive interference produces
the dark fringes. Dark fringes in the diffraction pattern of a
single slit are found at angles θ for which
w sinθ = mλ,
where m is an integer, m = 1, 2, 3, ... .
For the first dark fringe we have w sinθ = λ.
When w is smaller than λ , the equation w sinθ = λ has no solution and no dark fringes are produced.
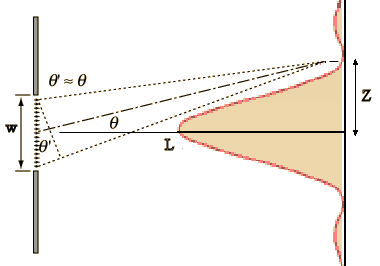If the interference pattern is viewed on a screen a distance L from the
slits, then the wavelength can be found from the spacing of the fringes. We have
λ = w sinθ/m and sinθ = z/(L2
+ z2)½), or
λ = zw/(m(L2 + z2)½),
where z is the distance from the center of the interference pattern to the
mth dark line in the pattern.
If L >> z then (L2 + z2)½ ~ L and we can write
λ = zw/(mL).
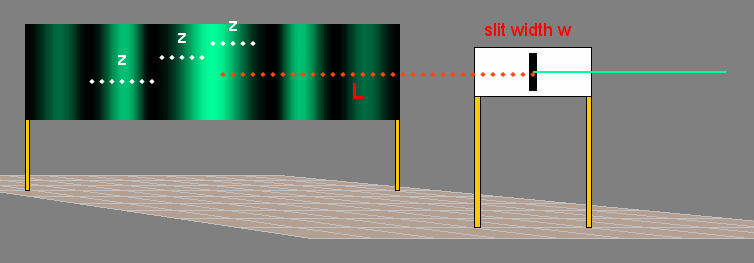
Note: The diffraction pattern is symmetric. Fringes appear at the
same angles or distances on either side of the central maximum.
Please watch: Diffraction of Light -
Exploring Wave Motion (YouTube)
External link:
Diffraction Demo: Single Slit and Circular Aperture (Youtube)
Problem:
When a monochromatic light source shines through a 0.2 mm wide slit onto a
screen 3.5 m away, the first dark band in the pattern appears 9.1 mm from the
center of the bright band. What is the wavelength of the light
Solution:
- Reasoning:
Dark fringes in the diffraction pattern of a single slit are found at angles
θ for which w sinθ = mλ, where m is an integer, m = 1, 2, 3, ... .
For the first dark fringe we have w sinθ = λ. Here we are asked
to solve this equation for λ.
- Details of the calculation:
z = 9.1 mm = 9.1*10-3 m.
L = 3.5 m.
w = 0.2 mm = 2*10-4 m.
L >> z, therefore sinθ ~
z/L and λ = zw/(mL).
λ = (9.1*10-3 m)(2*10-4
m)/(3.5 m).
λ = 5.2*10-7
m = 520 nm.
Problem:
Consider a single slit diffraction pattern for a slit width w. It is
observed that for light of wavelength 400 nm the angle between the first minimum
and the central maximum is 4*10-3 radians. What is the value of w?
Solution:
- Reasoning:
Dark fringes in the diffraction pattern of a single slit are found at angles
θ for which w sinθ = mλ, where m is an integer, m = 1, 2, 3, ... .
For the first dark fringe we have w sinθ = λ. Here we are asked
to solve this equation for w.
- Details of the calculation:
First minimum: w sinθ = λ, w = (400 nm)/sin(4*10-3
radians) = 1*10-4 m.