Wave energy and momentum

Electromagnetic waves transport energy through space. In free space this energy is transported by the wave with speed c. The magnitude of the energy flux S is the amount of energy that crosses a unit area perpendicular to the direction of propagation of the wave per unit time. It is given by the energy density times the speed c.
The energy per unit volume in the electric field is u_E = ½ε₀E²,
the energy per unit volume in the magnetic field is u_B = B²/(2μ₀), and B = E/c.
We also have μ₀ε₀ = 1/c². We can therefore write

S = c(u_E + u_B) = ½(cε₀E² + E²/(cμ₀)) = ½(cε₀E² + cε₀E²) = cε₀E² = EB/μ_0.The units of the energy flux S are J/(m²s) = W/m².

EM waves transport energy and deliver it when absorbed.
The energy flux vector is S. It has magnitude S and points in the direction of propagation, i.e. in the direction of E × B.
It is called the Poynting vector and can also be written as

S = (E × B)/μ₀.

For a sinusoidal plane wave both E and B vary as a function of time as sin(kx - ωt + φ), and S varies as sin²(kx - ωt + φ).
To find the magnitude of the average energy flux or intensity (I) of the wave we average sin²(kx - ωt + φ) over each period, which yields ½. Then

I = <S> = ½(cε₀E_max²).

Note: The energy transported by an electromagnetic wave is proportional to the square of the amplitude, E_max², of the wave.

Remember: For all waves, the energy transported is proportional to the square of the amplitude.

Problem:

How much electromagnetic energy per cubic meter is contained in sunlight if the intensity of the sunlight at the earth's surface under a fairly clear sky is 1000 W/m²?

Solution:

Reasoning:
The intensity <S> is the energy per unit area per unit time or the power per unit area. Multiplying <S> by the time ∆t yields the energy that falls on an unit area in the time ∆t. This energy is contained in a volume of unit area and height h, where h = c∆t. Light travels with speed c, so it travels a distance of h = c∆t in a time interval ∆t.
Details of the calculation:
If we set h = 1 m, then ∆t = (1/3)*10^-8s.
So Energy = <S>*(1/3)*10^-8s *(1 m²) is the energy that is contained in a cubic meter.
Energy = (1000 W/m²)*(1/3)*10^-8s*(1 m²) = 3.33*10^-6J.

Problem:

Assume the helium-neon lasers commonly used in student physics laboratories have power outputs of 0.5 mW.
(a) If such a laser beam is projected onto a circular spot 1 mm in radius, what is its intensity?
(b) Find the peak electric field strength.
(c) Find the peak magnetic field strength.

Solution:

Reasoning:
Intensity I = energy/(area*time) = power/area. The intensity is proportional to the square of the field amplitude.
Details of the calculation:
(a) Intensity I = power/area = 0.5*10^-3 W/(π*10^-6 m²) = 1.59*10² W/m².
(b) I = ½(cε₀E_max²).
E_max² = 2I/(cε₀) = (2*1.59*10³ W/m²)/(3*10⁸ m/s *8.854*10^-12 C/(V m) = 1.2*10⁵ N²/C².
E_max = 346 N/C.
(c) B_max = E_max/c = (345 N/C)/(3*10⁸ m/s) = 1.15*10^-6 T.

The radiation field E_rad produce by accelerating charges decreases as 1/r. Since the intensity is proportional to E_rad², the intensity of the radiation very far from a localized source therefore decreases as 1/r², where r is the distance from the source. Energy is conserved. As the EM wave propagates away from the source, its spreads its energy over a spherical surface A = 4πr², and therefore the energy per unit area decreases as 1/r².

Embedded Question 1

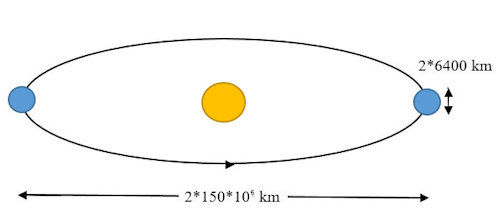
The sun emits electromagnetic radiation uniformly in all directions. Given the distance from the sun to the Earth of about ~150*10⁶ km, and the mean radius of the Earth of about 6400 km, what fraction of the sun's radiation falls on the Earth?

Discuss this with your fellow students in the discussion forum!
Consider the geometry and energy conservation.

Problem:

If the intensity of the sunlight at the earth's surface is 1000 W/m², what is the rate P at which the sun radiates light energy in W?

Solution:

Reasoning:
At a distance r from the Sun, the light energy emitted by the Sun has spread over an area of 4πr², the surface area of a sphere with radius r, centered at the Sun.
Details of the calculation:
The average Earth-Sun distance is R = 1.496*10⁸ km. So at the earth distance R, the intensity is I = P/(4πR²), where P is the power of the sun, (the rate at which it emits light energy.)
We have P = I*4πR² = (1000 W/m²)*4π(1.496*10¹¹ m)² = 2.81*10²⁶ W.
(The total energy output (not just visible light) of the Sun is 3.86*10²⁶ W.)

Summary: EM waves transport energy and deliver it when absorbed. The average energy flux is I = <S> = ½(cε₀E_max²).
Please watch this Youtube Video clip about using sunlight to melt rock.

Electromagnetic waves transport energy. EM wave also transport momentum. The magnitude of the momentum flux is <S>/c. It is the amount of momentum that crosses a unit area perpendicular to the direction of propagation of the wave per unit time. If an electromagnetic wave is absorbed, momentum conservation requires that the object acquires momentum. The object is therefore acted on by a force, F = ∆p /∆t. The radiation exerts radiation pressure P = F/A on the object. If the radiation is reflected instead of absorbed, then its momentum changes direction. The radiation pressure on an object that reflects the radiation is therefore twice the radiation pressure on an object that absorbs the radiation.

Problem:

A plane electromagnetic wave of intensity 6 W/m² strikes a small pocket mirror of area 40 cm² held perpendicular to the approaching wave.
(a) What momentum does the wave transfer to the mirror each second?
(b) Find the force that the wave exerts on the mirror.

Solution:

Reasoning:
EM waves transport momentum. The momentum flux is <S>/c. The wave is reflected by the mirror. The momentum transferred to the mirror per unit area per second is twice the momentum of the light striking the mirror per unit area per second.
Details of the calculation:
(a) ∆p/∆t = 2(1/c)<S>A.
<S>A = (6 W/m²)(4*10^-3m²) = 0.024 W.
∆p/∆t = 2*0.024 W/(3*10⁸m/s) = 1.6*10^-10kgm/s².
Each second the wave transfers 1.6*10^-10kgm/s of momentum to the mirror.
(b) F = ∆p/∆t = 1.6*10^-10N.

Please watch this Youtube video clip. Optical tweezers are be used to trap, move and sort live cells, organelles and large biomolecules. The cells interact with light and change the momentum of a focused laser beam. This change in momentum of the laser beam per unit time provides the tweezer force.
This tweezer force is small, but large enough to manipulate cells that are floating in a liquid.