In this studio session you will analyze the performance of a simple heat engine and review the various ways to state the second law of thermodynamics.

Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions.  Address the points highlighted in blue.  Answer all questions.

A heat engine

How can we do work with heat?  How can we convert some disordered energy back into ordered energy?

In this exercise you will analyze data obtained with is a "real" thermal engine that can be taken through a four-stage expansion and compression cycle and that can do useful mechanical work by lifting small masses from one height to another.  You will determine the useful mechanical work done by the engine by measuring the vertical distance y a mass m is lifted.  You will compare this mechanical work W_mech = mgy to the net thermodynamic work done during a cycle.  The pressure as a function of volume is recorded for one cycle, and the net thermodynamic work done by the engine equals the enclosed area on the PV diagram.
W = ∑_jP_jΔV_j.  We sum the work done during a large number of small changes of the volume.

The PASCO TD-8572 Heat Engine/Gas Law Apparatus is used to obtain the data.  The heart of this apparatus is a nearly friction-free piston-cylinder system.  The graphite piston fits snugly into a precision-ground Pyrex cylinder so that the system produces almost friction-free motion and negligible leakage.  The Heat Engine/Gas Law Apparatus is designed with two pressure ports with quick-connect fittings for connecting to an air chamber and a pressure sensor with tubing.

Your instructor will take you through a cycle of the PASCO TD-8572 Heat Engine.  (For a short video of data acquisition click here.)

After you have made your measurements, the instructor will also demonstrate two different types of real working heat engines to you.

Experiment

Procedure:

With no mass on the platform, the piston is raised ~4 cm, and the air chamber with tubing is connected to the engine.  The piston stays at a height of ~4 cm.

The computer is set up to record the pressure with respect to some reference pressure (in units of kPa), the volume of the gas in the cylinder with respect to some reference volume (in units of cm³), and the position of the cylinder above its starting position (in units of m) as a function of time and to produce plots of pressure versus volume and position versus time.

Measurement:

• Data acquisition starts. 
  Click on the thumbnails to see a larger picture.

  (a)	(b)	(c)	(d)	(e)

  (a)  The air chamber is placed into ice water.
  (b)  A 100 g mass is placed on the platform.  The weight of the mass increases the pressure at constant temperature, and the volume and therefore the height of the piston decrease by some amount.
  (c)  The air chamber is placed into hot water.  The temperature rises and the gas expands.  The volume and therefore the height of the piston increase.
  (d)  When the volume is no longer increasing, the mass is removed from the platform. Removing the weight decreases the pressure at constant temperature, and the volume and therefore the height of the piston increase by some amount.
  (e)  The air chamber is placed back into the ice water.  The temperature decreases and the gas contracts.  The volume and therefore the height of the piston decrease.

• When the piston has returned to the original position data acquisition stops.  (For a short video of data acquisition click here.)
• The computer has produced the plots shown below.

  Plot of pressure versus volume:
  
  

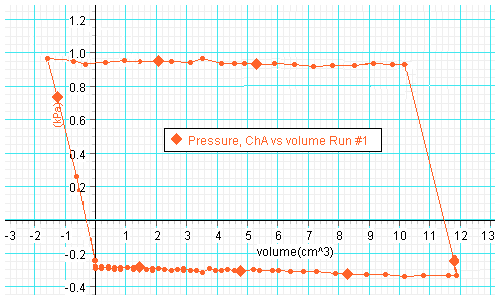
  Plot of piston position versus time:

  

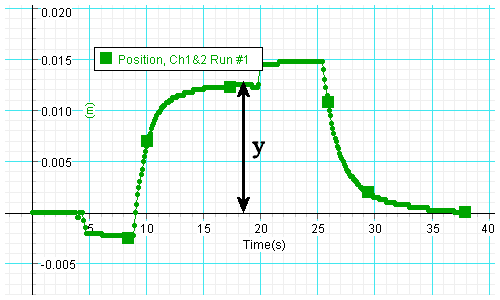
Data analysis:

• Determine the enclosed area on your P-V diagram.  (Estimate the area of the parallelogram by multiplying its width by its height.)  The y-axis has units of kPa and the x-axis has units of cm³.
  The area therefore has units of (kPa)(cm³) = (1000 N/m²)(10^-6 m³) = 10^-3 Nm = 10^-3 J.
  Determine the area in units of J.  This area represents the work done by your heat engine.  Record it in a table.
• From the position versus time graph determine the distance y the mass has been lifted, i.e. the difference in the positions of the platform just before the mass was put on and just before it was taken off the platform.  (The y-axis in this graph has units of m.)
• Find the change in potential energy mgy of the mass (in units of J), which is equal to the mechanical work done on the mass.  Record it in a table.
• Calculate the %difference between the two values.
  

Paste your table into your Word document and answer the following questions.

• The engine starts with an empty platform and the air chamber in ice water.  What happens  to the pressure and the volume when the mass is placed on the platform?
• What happens to the pressure and the volume as the air chamber is moved from the cold into the hot water?
• What happens to the pressure and the volume as the mass is removed from the platform?
• What happens to the pressure and the volume as the air chamber is moved back into the ice water?
• How does the thermodynamic work compare to the useful mechanical work?   What about conservation of energy?

Exercise

We can state the second law of thermodynamics in various ways. 

• Heat cannot, of itself, flow from a cold to a hot object.
• Heat cannot be taken in at a certain temperature with no other change in the system and converted into work.
• The total entropy of a closed system is always increasing.

How do we connect heat flow and entropy?

Discuss and answer all questions (blue font color).

(a)  Assume 50 students registered for a course.  You need to report the total number of students who actually attend.  You have every student in attendance sign a list.

• Which of the following would constitute a macrostate description of the class attendance and which would constitute a microstate description?
  • A list of the names of each student present today. 
  • The number of students in attendance.

(b)  Consider the following macrostates of the class.

1. All 50 students are present. 
2. 25 students are present. 
3. 1 student is present. 
4. No students are present.

• Which macrostate(s) would have the highest number of microstates?
• Which macrostate(s) would have the lowest number of microstates?

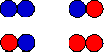(c)  Assume you have two boxes and you have to place a coin into each box.  You toss a coin and place it into box 1 without changing its orientation.  The side of the coin facing up can be either head (blue) or tail (red).  Then you toss a second coin and place it into box 2 without changing its orientation.  You are interested in how many coins end up "head up" or blue.  There are 4 different microstates.

• How many macrostates are there and what is the multiplicity Ω of those macrostates, i.e.  how many microstates correspond to each macrostate?

(d)  Now assume that you have a 6 by 6 array of squares.  You number the squares from 1 to 36.  You toss a coin and place it onto square 1 without changing its orientation.  The side of the coin facing up can be either head (blue) or tail (red).  You keep tossing coins and placing them in succession onto squares 2 through 36 without changing their orientation.  Each square holds exactly one coin. 
To specify the microstate of the array after you finished this process you have to list the color of each square.  Many different patterns (microstates) are possible, such as the ones shown on the right.  Every particular pattern is equally likely to occur.  There are 2³⁶ = 6.87*10¹⁰ possible patterns and the probability of observing any particular pattern is 1/2³⁶ = 1.46*10^-11.

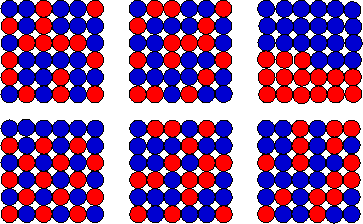Suppose you are only interested in the macrostate, i.e. you are only interested in how many squares are red.  Most macrostates correspond to many microstates.  A few of the allowed microstate for the "15 red squares" macrostate are shown on the right.
 

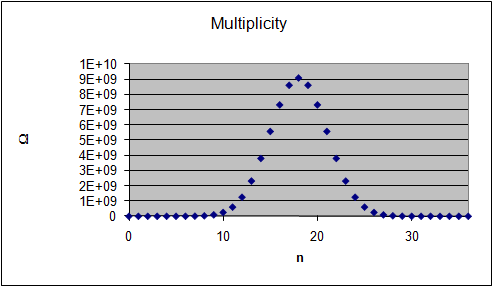
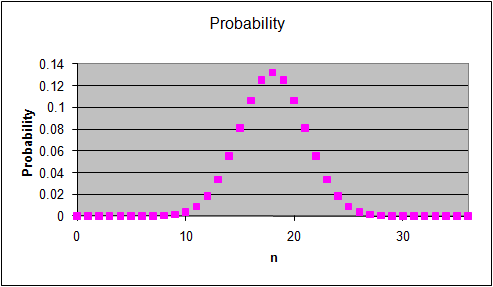
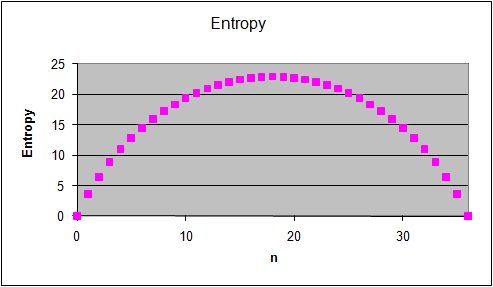
The graphs on the right show the multiplicity Ω for each "n out of 36" macrostate, the probability of observing this macrostate and its entropy S = lnΩ.
(The entropy of a macrostate is defined as S = k_B lnΩ, where k_B is the Boltzmann constant.  Let us measure S in units of k_B and use S = lnΩ.)

Which statement below best describes the relationship between probability and entropy for the macrostates we are considering?

1. The most probable macrostates have the lowest entropy.
2. The most probable macrostates have the highest entropy.
3. There is no clear relationship between entropy and probability for these macrostates.

If we examine the probabilities for all of the macrostates in the system we find that the probability is

1. spread evenly among all of the macrostates.
2. spread out among a large fraction of the macrostates, but with some macrostates having slightly higher probabilities than others.
3. concentrated within a small fraction of the macrostates centered on a most probable macrostate.
4. entirely concentrated into a single most probable macrostate.

How does this behavior scale with the number of coins N?

• If you have N squares and N coins, the most probable number "head up" coins is N/2.  The spread of the distribution increases a N^½, so the percentage spread decreases as N^-1/2. 
• For 36 square, the spread approximately plus or minus 6, the percentage spreads is (1/6)*100% or 16.6%.  That means that if n differs by more than 16.6% from 18, then it is not very likely to occur.
• If there were N = 10²⁴ squares and coins (just as there might be 10²⁴ molecules in a gas), then the percentage spread is (10^-12)*100% = 10^-10%, that means in n differs from N/2 by more than 10^-10% from 0.5*10²⁴, it is not very likely to occur.

(e)  Consider approximately 10²⁴ gas molecules in a box.  A divider which can conduct heat, for example a rubber diaphragm, separates the box into two chambers of equal size.  Each chamber contains half of the molecules.  Assume that the internal energy of the gas is (approximately) fixed.

• Describe some possible macrostates of the gas in the two chambers of the box.
• Describe a low entropy macrostate.
• Describe a high-entropy macrostate.
• In which situation described below is the entropy of the gas greatest?
  1. When the energy is spread nearly evenly among all the molecules and all the molecules are clustered in small regions of each chamber.
  2. When the energy is concentrated in a small number of molecules that are spread nearly evenly throughout the box.
  3. When the energy is spread nearly evenly among all the molecules and all the molecules are spread nearly evenly throughout the box.
  4. When the energy is concentrated in a small number of molecules which are clustered in a small region of one chamber of the box.

Newton's laws work equally well backwards in time as they do forwards.  If a sequence of motions and interactions leads to an increase in entropy, then the time-reversed sequence will lead to a decrease in entropy.  Both sequences are allowed by Newton's laws. 

• Why does heat, of itself, not flow from a cold to a hot object, if it is allowed by Newton's laws?
• What, do you think, determines, the rate of change of the entropy of a system?

Entropy can decrease locally (in a subsystem).  Heat can be moved from a cold place to a hot place.  (We all are familiar with refrigerators and heat pumps.)  But it takes ordered energy that comes from outside the subsystem.  For the entropy of a subsystem to decrease, the system as a whole must not yet have reached a state of maximum entropy.

Convert your log into a lab report.

Name:
E-mail address:

Laboratory 10 Report

• In one or two sentences, state the goal of this lab.
• Make sure you completed the entire lab and answered all parts.  Make sure you show your work and inserted and properly labeled relevant tables and plots.
• Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab10.docx), go to Canvas, Assignments, Lab 10, and submit your document.