Lab 8

In this lab, you will explore fluid flow using a simulation.  Then you will determine the viscosity of a brand of "Volumizing Shampoo" using Stokes' law.  You will use a fluid column as a viscometer and measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the fluid, after the sphere has reached terminal velocity.

Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions.  This log will form the basis of your lab report.  Address the points highlighted in blue.  Answer all questions.

The equation of continuity

Liquids are incompressible.  Their density ρ = mass/volume is constant.  When a liquid flows through a pipe, conservation of mass leads to the equation of continuity.
Consider the flow of a fluid through a pipe with varying cross sectional area A.
The volume V1 of liquid flowing into the pipe equals the volumeV2 flowing out of the pipe per unit time.
V1/Δt = V2/Δt,  A1Δx1/Δt = A2Δx2/Δt,  A1v1 = A2v2.


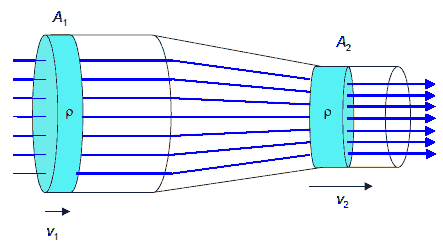
image

For the pipe we write the equation of continuity as A1v1 = A2v2, or Q = Av = constant.  Q is called the volume flow rate.

Open the simulation
http://phet.colorado.edu/en/simulations/fluid-pressure-and-flow
to investigate the flow of a liquid in a pipe.

The interface

Flow tab

Water Tower tab

Exploration 1:

Click the Flow tab.

Part (a)

Table 1

  density pipe diameter (m) flow speed (m/s) pressure (kPa) flow rate
Q = vA m3/s)
case 1 water        
case 2 water        
case 3 water        
case 4 gasoline        
  honey        

From your measurements, for all cases, calculate the volume flow rate in m3/s and record it in the table.

Insert your table into your log.  Answer the following question.

Part (b)

Reset all.

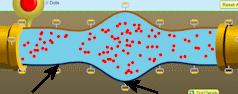
image

Table 2

  density pipe diameter (m) flow speed (m/s) pressure (kPa) flow rate
Q = vA (m3/s)
location 1 water        
location 2 water        

Insert your table into your log.  Answer the following question.

Part (c)

Now reset all.  Turn on friction.  Adjust the flow rate so that the speed as close to the wall of the straight pipe as you can measure is 0.6 m/s. 

Exploration 2

Click the Water Tower tab.

Do some exploring!  Fill the tank.  Let the water partially drain out by opening the hole in the bottom of the tank.  Match the leakage to keep water level in the tank constant.  Raise and lower the tank.  Measure the speed of the fluid just as its exits the tank and the horizontal distance the water travels until it hits the ground.

Answer the following questions.

Viscosity

Viscosity is a measure of a fluids resistance to relative motion within the fluid.  Highly viscous fluids do not readily flow.  The viscosity of a fluid usually varies with temperature.  For a fluid flowing through a pipe in laminar flow, viscosity is one of the factors determining the volume flow rate.

Poiseuille's law: Q = π∆Pr4/(8ηL)

Volume flow rate = π*(pressure difference)*(pipe radius)4/[8*(pipe length)*viscosity)

Exercise

Blood is a viscous fluid circulating through the human body.  The circulatory system is a closed-loop system with two pumps.  One-way valves keep the flow unidirectional.  A sketch is shown below.  The unit of pressure in the sketch is mm Hg.  (1 atm = 760 mm Hg)


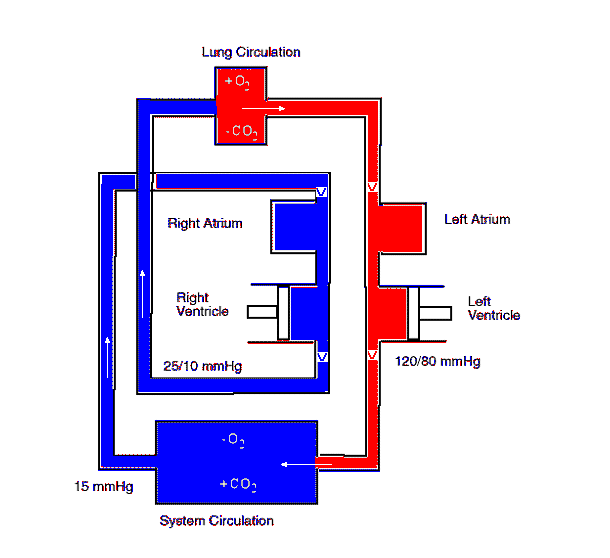
image

During heavy exercise, the blood's volume flow rate is 5-10 times higher than when the body is at rest.  Discuss different possible ways that a body can accomplish this?

Record your explanations in your log.

It is often important to know the viscosity of a fluid.  A viscosimeter is the instrument used to measure viscosity.  The study of the viscosity of substances is known as rheology.

Example:

In order to keep the pistons moving smoothly in the cylinders of the internal combustion engine in a car, a thin film of motor oil between the piston rings and the cylinder wall acts as a lubricant.  The oil must be able to keep the piston moving smoothly, when the engine first starts up and is still cold and when the engine reaches its high operating temperature.  One way of measuring an oil's ability to lubricate is to measure its viscosity.

In this session you will determine the viscosity of different brands of "Volumizing Shampoo" using Stokes' law.  You will use a fluid column as a viscometer and measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the fluid, after the sphere has reached terminal velocity.

George Gabriel Stokes, an Irish-born mathematician, worked most of his professional life describing fluid properties.  Stokes' law gives the force required to move a sphere through a viscous fluid at a specific velocity, as long as the flow around the sphere is laminar and the Reynolds number is low (Reynolds number < 1).  Stokes' Law is written as

F = 6πηrv.

Here r is the radius of the sphere, v the speed and η the viscosity. 

Experiment

Measure the rate of descent of a steel sphere, as it falls under the influence of gravity through the shampoo.

image   image

Do the experiment!  Find the speed (positive number) of the sphere.

Data Analysis:

The forces acting on the sphere are gravity, the buoyant force, and the viscous drag force given by Stokes' law.  A free body diagram is shown below.


image

Since the sphere moves with constant velocity, the net force is zero. 

The density of the "Volumizing Shampoo" is very close to that of water, ρfluid = 1.03 g/cm3.
The density of the stainless steel ball is 7.866 g/cm3, and its diameter is 1/4 inch = 0.635 cm.

fluid viscosity (Pa-s)
honey 2 - 10
molasses 5 - 10
ketchup 50 - 100
chocolate syrup 10 - 25

Convert your log into a lab report.

Name:
E-mail address:

Laboratory 8 Report

Save your Word document (your name_lab8.docx), go to Canvas, Assignments, Lab 8, and submit your document.