Studio session 11

Mechanical Waves

A wave pulse is a disturbance that moves through a medium.  A periodic wave is a periodic disturbance that moves through a medium.  The medium itself goes nowhere.  The individual atoms and molecules in the medium oscillate about their equilibrium position, but their average position does not change.  If the displacement of the individual atoms or molecules is perpendicular to the direction the wave is traveling, the wave is called a transverse wave.  If the displacement is parallel to the direction of travel the wave is called a longitudinal wave or a compression wave.

Waves can transport energy and information.  Examples of mechanical waves are water waves, sound waves, and seismic waves. All waves are described mathematically in terms of a wave function, and reflection, refraction and diffraction and interference a characteristic behaviors of all types of waves.

In this session you will study wave motion in one dimension only, to learn about several of these characteristic behaviors.  You will visualize the patterns of pressure variations associated with different sounds traveling through air and you will examine the frequency content of those patterns.  You will produce standing sound waves in a tube and measure the speed of sound waves in air.

Equipment needed:

Open a Microsoft Word document to keep a log of your experimental procedures, results and discussions.  Address the points highlighted in blue.  Answer all questions.

Exploration

Use an on-line simulation from the University of Colorado PhET group to explore the behavior of waves on a string.
Link to the simulation: http://phet.colorado.edu/en/simulations/wave-on-a-string

(a)  Explore the interface.  Try the different controls.

(b)  Investigate the behavior of a wave pulse.

(c)  Investigate the behavior of a traveling wave.

  wave 1 wave 2 wave 3 wave 4 wave 5
amplitude A          
wavelength λ          
period T          
frequency f          
speed v          

(d)  Investigate the behavior of a standing wave.

Sound

Experiment 1

Most sounds we hear are not single sound pulses but more complex sound patterns.  We will now explore some of those sound patterns.

(a)  Compare the output of a sound sensor (microphone) for a clapping and a humming sound.  The sound sensor is an electrets condenser microphone which converts pressure variations into voltage variations which can be recorded and displayed by the computer.

Paste your graphs into your Word document.  How do the microphone voltage patterns compare?  Describe your observations.

(b)  Compare the output of a sound sensor for a humming sound and the sound produced by a tuning fork.

Paste your graph into your Word document.  Does your humming sound wave have a definite frequency?  How do you justify your answer?

Paste your graph into your Word document.  Does the tuning fork producing a pure sine wave?  How does the wave of the tuning fork sound compare to the waveform of the humming sound?

(c)  Any wave pattern can be produced by superimposing the appropriate sinusoidal waves.  Breaking up the original sound wave into its sinusoidal components is called Fourier analysis.  We can find the frequencies and amplitudes of the sine and cosine waves that must be added to produce our sound wave.  We will choose the "Fast Fourier Transform" or FFT display to let Capstone perform Fourier analysis on a sound.

Paste your graphs into your Word document.  What frequencies are strong in your "ahhh" sound?

What frequencies are present in this signal?

What happens to the frequencies shown in the FFT?

Experiment 2

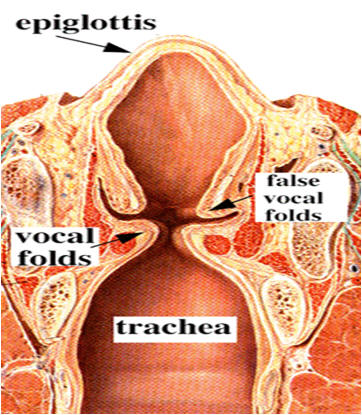imageWhen you produce a sound, air from the lungs is pushed through the vocal folds.  This produces a train of air pulses.  As you speak, muscles in your larynx tighten the vocal folds.  When air from your lungs passes through the folds, they vibrate.  Vibrations at the resonance frequencies have the largest amplitudes.  The tighter the vocal cords, the higher are the resonance frequencies and the higher is the pitch of your voice.

The pulse train produced by the vocal folds is shaped by the resonances of the vocal tract.  The vocal tract acts like a variable filter.  It is a filter because it amplifies certain frequencies and suppresses others.  It is variable because by changing the position of your tongue, jaw, lips, etc.  you can change the overall frequency response.

Link: The Human Voice

Develop a hypothesis to explain the frequency pattern observed when you make the "ahhh" sound.

 

 

You will now use a resonance in a tube as a variable filter.  The tube has one open and one closed end.  The length of the tube can be varied by moving a piston. You will produce resonances for a fixed frequency by varying the length of the tube.

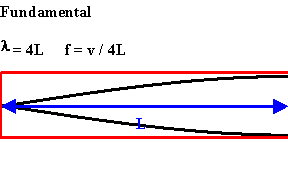
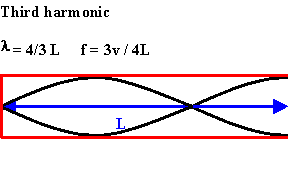
image          image


image

Table 1 (tube length)

  1st harmonic 3rd harmonic 5th harmonic frequency (Hz) temperature oC
fork 1          
fork 2          

Analyze your data and complete table 2.

Table 2

  frequency f wavelength λ temperature TC speed v = λf
fork 1        
fork 2        

Compare your experimentally obtained value for the speed of sound with the value obtained from the formula
v = (331.4 + (0.6/oC)TC) m/s.

Experiment 3

In the previous experiment you measured the speed of sound by measuring the wavelength and frequency of a sinusoidal wave and using v = λf.  In this experiment you will measure the speed of sound directly.

Move the piston as far as possible to one end of the resonance tube.  Set up the microphone at the open end of the tube.  Your goal is to record the sound of your fingers snapping and then the echo of the snap after it has traveled the length of the tube and back.


image

 

Convert your log into a lab report.

Name:
E-mail address:

Laboratory 11 Report

Save your Word document (your name_lab11.docx), go to Canvas, Assignments, Lab 11, and submit your document.