In this studio session In this session, you will try to verify the equation
of continuity for water flowing out of the bottom of an elevated can through a
small-diameter hose. You will measure the fraction of the ordered
energy that is lost because of friction. You will also explore fluid flow using a simulation. Then you will determine the viscosity of
different brands of "Volumizing Shampoo" using
Stokes' law. You will use a fluid column as a viscometer and measure the
rate of descent of a steel sphere, as it falls under the influence of gravity
through the fluid, after the sphere has reached terminal velocity.
Equipment needed:
- can and hose
- water container
- meter stick
- Shampoo bottle with metal sphere and linear scale
- Magnet
- Webcam
Open a Microsoft Word document to keep a log of your
experimental procedures, results and discussions. This log will form the basis of
your lab report. Address the points highlighted in blue. Answer all questions.
The equation of continuity
Liquids are incompressible. Their density ρ = mass/volume is constant.
When a liquid flows through a pipe, conservation of mass leads to the
equation of continuity.
Consider the flow of a fluid through a pipe with varying cross sectional area A.
The volume V1 of liquid flowing into the pipe equals the volumeV2 flowing out of the pipe per unit time.
V1/Δt = V2/Δt, A1Δx1/Δt = A2Δx2/Δt, A1v1 = A2v2.
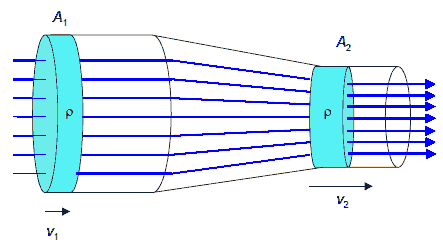
For the pipe we write the equation of continuity as
A1v1 = A2v2,
or Q = Av = constant. Q is called the volume flow rate.
Experiment 1
Each table will work as a group on this experiment.
One end of a rubber hose is attached to a can with a spout in the bottom.
The can has an inside diameter of d1 = 9.8 cm
and the rubber hose has an inside diameter of d2
= 0.8 cm. The other end of the hose is taped to a horizontal rod a
certain distance below the can. While one member of your group plugs the
hose with a finger, another member fills the can with water. Then you will
allow the water to drain from the can through the hose into a catch pan.
You will measure the speed with which the water level in the can drops, and the
speed with which the water emerges from the hose.
Set up the apparatus on the floor, not on the table.
- The horizontal position of the lower end of the hose should be a few cm
over the edge of the catch pan.
- Measure the height of ∆y of the
center of the hose above the bottom of the catch pan.
- Measure the vertical distance h from the
center of the hose to the center of the 5 cm
long black tape inside the can.
- Record your measurements of ∆y and h in table 1.
Table 1
| can diameter (cm) |
9.8 |
| hose diameter (cm) |
0.8 |
| tape length (cm) |
5 |
| ∆y (cm) |
|
| h (cm) |
|
| ∆t (s) |
|
| ∆x (cm) |
|
Fill up the can with water to above the upper end of the black tape without
allowing water to drain. Distribute tasks to be performed after you start
draining the water.
- One member of your group will notify the others when the water level in
the can reaches the upper end and when it reaches the lower end of the black tape.
- Several members will measure the time interval ∆t between these two events.
- Other members will mark the spots where the water hits the bottom of the
pan for those two events. You will have to determine the average
horizontal distance ∆x between the lower end of
the hose and the spots where the water hits the pan.
Drain the water while making measurements and record your measurements
of ∆x and ∆t in the table.
- Repeat the experiment to check for reproducibility.
Data Analysis:
- To find the speed v1 with which the water level drops calculate v1 = (5 cm)/∆t.
- To find the speed v2 with which the water emerges from the hose, use the formulas for projectile motion.
- For the vertical motion we have ∆y = ½gt2.
We can solve for the time t it takes water to fall from the end of the
hose to the bottom of the pan.
- For the horizontal motion we have ∆x = v2t.
Inserting the time from above we have v2
= ∆x/(2∆y/g)1/2.
- The kinetic energy of a volume V of water moving with speed v = ½ρVv2
= ½mv2, since ρV = m.
The potential energy of the water changes as it moves. While all the
water moves, the change in potential energy is the same as that of a volume
V, which has been moved from the top of the can to the exit of the hose.
The potential energy of the water in the rest of the can and hose is the
same as the potential energy of the water that used to be there before the
movement.
The change in the potential energy of a mass ρV = m of water coming out
of the hose is mgh.
Here h is the distance from the
center of the hose to the center of the 5 cm long black tape inside the can
that you measured earlier.
If no ordered energy is converted into disordered energy we expect from
energy conservation that the change in kinetic energy is equal to the change
in potential energy.
½mv22 - ½mv12 = mgh or ½(v22
- v12) = gh.
But some of the ordered energy will be converted into disordered energy, so
we expect ½(v22 - v12) < gh.
Dividing the change in kinetic energy by the change in potential energy we find the fraction R = (v22 - v12)/(2gh) of the potential energy that is converted to
kinetic energy. If no ordered energy is lost, then R = 1. We
expect it to be less than one, because friction is always present. But how much less?
Fill in table 2.
Table 2
| v1 = 5/∆t (cm/s) |
|
| v2 = ∆x/(2∆y/980)1/2 (cm/s) |
|
| A1v1 = (πd12/4)v1 (cm3/s) |
|
| A2v2 = (πd22/4)v2 (cm3/s) |
|
| R = (v22 - v12)/(2*980*h) |
|
Results:
- Did you verify the equation of continuity? If not, explain what factors may be responsible for the difference in your two values of the
volume flow rate? Does the difference seem reasonable considering those factors?
- What fraction of the potential energy of the water is converted into kinetic
energy in this experiment? What fraction is converted into thermal
energy? Does this result surprise you? If yes, think about Poiseuille's law.
Open the simulation
http://phet.colorado.edu/en/simulations/fluid-pressure-and-flow
to investigate the flow of a liquid in a pipe.
The interface
- Try all the different tabs at the top of the simulation.
- "Reset All" resets only the tab that you are presently
using.
- You can use multiple tools to make measurements.
- Sensors are very sensitive, so you may expect some
variations in the readings.
Flow tab
- The handles on the "Flow" tab let you change the
shape/height of the water tube and end pipes.
- You can pause the simulation and then use increment time in
discreet steps.
Water Tower tab
- Water is allowed to flow out of a hole at the bottom of a
tall water tower.
Exploration 1:
Click the Flow tab.
Part (a)
- Reset all. Choose no friction. For the fluid density choose water.
Keep the flow rate at 5000 liter/s = 5 m3/s.
- Case 1
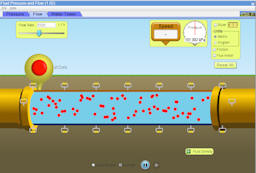
- Measure the diameter of the pipe and hose and the flow speed of the
fluid.
- Measure the pressure at the bottom of the pipe.
- Record all values in table 1.
- Click the red button to get a representation of the profile of the
flow.
- Case 2
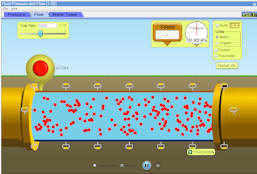
- Change the diameter of the pipe and hose by pulling all the lower handles down as far as possible.
- Measure the diameter of the pipe and hose and the flow speed of the
fluid.
- Measure the pressure at the bottom of the pipe.
- Record all values in table 1.
- Click the red button to get a representation of the profile of the flow.
- Case 3
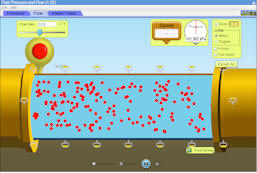
- Case 4
- Keep the diameter of the pipe and hose the same as in case 3.
- Change the fluid density first to gasoline and then to honey.
- Measure the flow speed of the fluid.
- Measure the pressure at the bottom of the pipe.
- Record all values in table 1.
- Click the red button to get a representation of the profile of the flow.
Table 1
| |
density |
pipe diameter (m) |
flow speed (m/s) |
pressure (kPa) |
flow rate
Q = vA (m3/s) |
| case 1 |
water |
|
|
|
|
| case 2 |
water |
|
|
|
|
| case 3 |
water |
|
|
|
|
| case 4 |
gasoline |
|
|
|
|
| |
honey |
|
|
|
|
From your measurements, for all cases, calculate the volume flow rate in m3/s
and record it in the table.
Insert your table into your log. Answer the following question.
- Do your measurements yield the same volume flow rate for all cases?
- For a given flow rate, how does the
flow speed change as the pipe diameter changes?
- For a given flow rate, how does the
pressure at the bottom of the pipe change as the pipe diameter changes?
- For a given flow rates and pipe
diameter, how does the pressure change as the fluid density changes?
- Describe the the profile of the flow. Is it the same for all
cases?
Part (b)
Reset all.
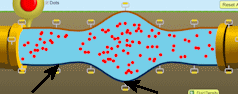
- Move the yellow handles in the middle of the pipe to
their extreme up and down positions, while leaving everything else untouched.
- Measure the pressure as close to the middle of the pipe as possible at
two different locations in the pipe near the handles pointed to by arrows in
the figure above.
- At the same locations, measure the diameter of the pipe and the flow
speed.
- Record your measurements in table 2 and calculate the volume flow rate
for both locations.
Table 2
| |
density |
pipe diameter (m) |
flow speed (m/s) |
pressure (kPa) |
flow rate
Q = vA m3/s) |
|
location 1 |
water |
|
|
|
|
|
location 2 |
water |
|
|
|
|
Insert your table into your log. Answer the following question.
- Did you verify the equation of continuity?
- At which location do you measure the higher pressure? What is the
pressure difference in kPa?
Part (c)
Now reset all. Turn on friction. Adjust the flow rate so that the
speed as close to the wall of the straight pipe as you can measure is 0.6 m/s.
- What is the speed of the liquid in the middle of the pipe
in m/s?
- Describe the the profile of the flow. Compare it to the
profile without friction.
- Comment on the effects of friction (viscosity).
Viscosity
Viscosity is a measure of a fluids resistance to relative motion
within the fluid. Highly viscous fluids do not readily flow. The viscosity of a
fluid usually varies with temperature. For a fluid flowing through a pipe
in laminar flow, viscosity is one of the factors determining the volume flow
rate.
Poiseuille's law: Q = π∆Pr4/(8ηL)
Volume flow rate = π*(pressure
difference)*(pipe radius)4/[8*(pipe length)*viscosity)
Exercise
Blood is a viscous fluid circulating through the human body. The
circulatory system is a closed-loop system with two pumps. One-way valves keep
the flow unidirectional. A sketch is shown below. The unit of pressure in
the sketch is mm Hg. (1 atm = 760 mm Hg)
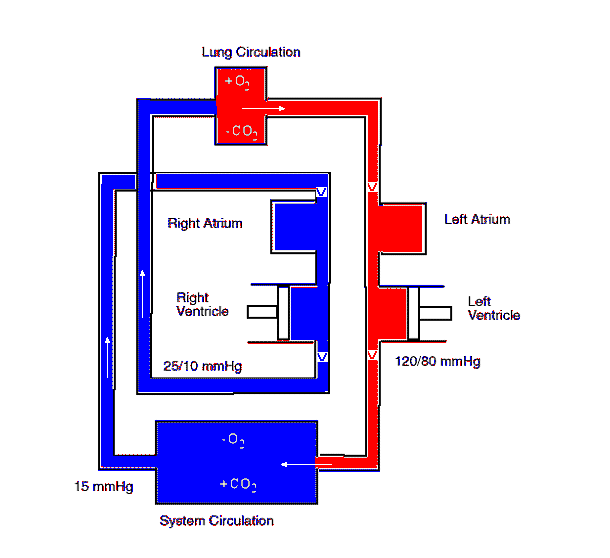
During heavy exercise, the blood's volume flow rate is 5-10 times higher
than when the body is at rest. Discuss different possible ways that a body
can accomplish this?
- Is increasing blood pressure 5 - 10 times higher a viable option?
What percentage increase in blood pressure is reasonable? Explain!
- Is decreasing the length of your blood vessels a viable option? Explain!
- The arterioles (small arteries) are surrounded by circular muscles.
In order to increase the blood flow rate by a factor of 5, what percentage
increase in the radius of a blood vessel is needed? (This is called vasodilatation.)
- Arteries in the human body can be constricted
when plaque builds up on the inside walls. How does this affect the blood flow
rate through this artery? Is it possible for the body to keep the flow
rate constant? Explain!
Record your explanations in your log.
It is often important to know the viscosity of a fluid. A viscosimeter
is the instrument used to measure viscosity. The study of the viscosity of
substances is known as rheology.
Example:
In order to keep the pistons moving smoothly in the cylinders of the internal
combustion engine in a car, a thin film of motor oil between the piston
rings and the cylinder wall acts as a lubricant. The oil must be
able to keep the piston moving smoothly, when the engine first starts up and is
still cold and when the engine reaches its high operating temperature. One
way of measuring an oil's ability to lubricate is to measure its viscosity.
In this session you will determine the viscosity of
different brands of "Volumizing Shampoo" using
Stokes' law. You will use a fluid column as a viscometer and measure the
rate of descent of a steel sphere, as it falls under the influence of gravity
through the fluid, after the sphere has reached terminal velocity.
George Gabriel Stokes, an Irish-born mathematician, worked most of his
professional life describing fluid properties. Stokes' law gives the force
required to move a sphere through a viscous fluid at a specific velocity, as
long as the flow around the sphere is laminar and the Reynolds number is low
(Reynolds number < 1). Stokes' Law is written as
F = 6πηrv.
Here r is the radius of the sphere, v the speed and η the viscosity.
Experiment 2
Measure the rate of descent of a steel sphere, as it falls under the
influence of gravity through the shampoo.
- Start with the steel sphere held near the middle of the lid of the
shampoo bottle
by the magnet. Make sure all the bubbles have risen and the fluid is
quiet.
- Connect a webcam to one computer.
- Start the Windows 10 Camera App and select "Take Video".
- If necessary, click the "Change Camera" icon to select the USB video device.
- Under Settings, select the video quality of 720p, 4:3, 30 fps.
- Position the camera so it has a good view of the shampoo bottle and the
scale.


- Remove the magnet and wait for the ball to drop. Make sure it does
not contact the wall of the bottle.
- When the ball has fallen ~2 cm start recording.
- Stop recording when the ball reaches the bottom of the bottle. Your
video clip is automatically saved in the Picture/Camera Roll directory.
- Close the Camera App and open the
this webpage.
- Open your recorded video. Step through it frame by
frame. The frame number and the time will be displayed. When the sphere is in front of
the scale at 12 cm, 11 cm, ..., 2 cm, record the frame number and time in an Excel
spreadsheet.
| position (cm) |
frame number |
time (s) |
| 12 |
|
|
| 11 |
|
|
| 10 |
|
|
| 9 |
|
|
| 8 |
|
|
| 7 |
|
|
| 6 |
|
|
| 5 |
|
|
| 4 |
|
|
| 3 |
|
|
| 2 |
|
|
- Plot position (vertical axis) versus time
(horizontal axis). Verify that the plot resembles a
straight line. This verifies that the sphere moves with constant,
terminal velocity. Find the speed of the sphere by adding a linear trendline. The magnitude of the slope of this trendline
is the speed (positive number) of the sphere.
Data Analysis:
The forces acting on the sphere are gravity, the buoyant force, and the
viscous drag force given by Stokes' law. A free body diagram is shown below.

Since the sphere moves with constant velocity, the net force is zero.
- Fdrag + Fbuoyant = mg
- 6πηrspherev + ρfluidVsphereg = ρsphereVsphereg
- 6πηrspherev + (4/3)πρfluid(rsphere)3g
= (4/3)πρsphere(rsphere)3g
- η = 2(ρsphere - ρfluid)(rsphere)2g/(9 v)
The density of the "Volumizing Shampoo" is very close to that of water,
ρfluid = 1.03 g/cm3.
The density of the stainless steel ball is 7.866 g/cm3, and its
diameter is 1/4 inch = 0.635 cm.
- Calculate the viscosity η of the shampoo using
your measured velocity in units of poise = g/(cm-s).
Use the densities in units of g/cm3, the speed in units of cm/s,
the radius of the sphere in units of cm and g = 981 cm/s2.
(1 Pa-s = 1 kg/(m s) = 10 g/(cm-s) = 10 poise)
- Calculate the Reynolds number R = 2ρfluidrspherev/η.
It is a dimensionless number.
Check that the Reynolds number is less than
1, so that we are in the regime where Stokes' law is valid.
- Compare your value for η with the value obtained by the other groups.
Do the values agree?
- The table below lists typical viscosities of some viscous fluids at room
temperature. Does your value for the viscosity of the shampoo seem
reasonable? Discuss.
| fluid |
viscosity (Pa-s) |
| honey |
2 - 10 |
| molasses |
5 - 10 |
| ketchup |
50 - 100 |
| chocolate syrup |
10 - 25 |
- Predict the terminal velocity of a sphere made of the same material but with
diameter of 3/8 inch in the same fluid.
Record your results and conclusions in your log.
Convert your log into a lab report.
Name:
E-mail address:
Laboratory 8 Report
- In one or two sentences, state the goal of this lab.
- Make sure you completed the entire lab and answered all parts. Make
sure you show your work and inserted and properly labeled relevant tables
and plots.
- Add a reflection at the end of your report in a short essay format.
Save your Word document (your name_lab8.docx), go to Canvas, Assignments, Lab
8, and submit your document.













