Vectors

In physics, quantitative models are developed on the basis of measurements. They need to be tested by making more measurements. Measurements are made in standard increments, called units. Without units a measurement is meaningless.

Some quantities are specified completely by a magnitude, which is to say by a number and the appropriate units.
A real number by itself is called a scalar, and such quantities are called scalar quantities. Symbols that denote these scalar quantities are normal letters.

Examples of scalar quantities:

temperature (T)  T = 10 ^oC
time interval (t)  t = 5 s
mass (m)             m = 3 kg

Other quantities are specified by a magnitude and a direction. By direction, we mean a direction in space.
Such quantities are called vector quantities. Symbols that denote these vector quantities are bold letters, or normal letters with arrows drawn above.

Examples of vector quantities:

displacement (d)   d = 10 m north
velocity (v)          v = 3 m/s eastward
force (F)              F = 9 N up

To uniquely specify vector quantities we need a reference point and reference lines, i.e. we need a coordinate system.

The Cartesian coordinate system is the most commonly used coordinate system. In two dimensions, this system consists of a pair of lines on a flat surface or plane, that intersect at right angles. The lines are called axes and the point at which they intersect is called the origin. The axes are usually drawn horizontally and vertically and are referred to as the x- and y-axis, respectively.

A point in the plane with coordinates (a, b) is a units to the right of the y axis and b units up from the x axis if a and b are positive numbers.
If a and b are both negative numbers, the point is a units to the left of the y axis and b units down from the x axis.
In the figure on the right point P₁ has coordinates (3, 4), and point P₂ has coordinates (-1, -3).
In three-dimensional Cartesian coordinates, the z-axis is added so that there are three axes all perpendicular to each other.

In the polar coordinate system, each point in the plane is assigned coordinates (r, φ) with respect to a fixed line in the plane called the axis and a point on that line called the pole. For a point in the plane, the r-coordinate is the distance from the point to the pole, and the φ-coordinate is the counterclockwise angle between the axis and a line joining the origin to the point.
The r-coordinate is always positive and the range of φ is from 0 to 2π (360^o). To be able to transform from Cartesian to polar coordinates and vice versa, we let the axis of the polar coordinate system coincide with the x-axis of the Cartesian coordinate system and the pole coincide with the origin.
In the figure on the right the Point P₁ has polar coordinates (r₁, φ₁) = (5, 53.1^o), and the point P₂ has polar coordinates (r₂, φ₂) = (3.16, 251.6^o ).
The transformation equations are

x = r cosφ, y = r sinφ.

r = (x²+ y²)^½, φ = tan^-1(y/x).

Cylindrical coordinates and spherical coordinates are two different extensions of polar coordinates to three dimensions.
Once we have picked a coordinate system, a physical vector quantity in two dimensions can be represented by a pair of numbers.
If we pick Cartesian coordinates, there numbers are the vector's projections on the axes of the Cartesian coordinate system.

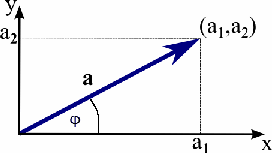The vector a in the figure on the right has x-component a₁ and y-component a₂.
Its length or magnitude is a = (a₁² + a₂²)^½. This follows from the Pythagorean theorem.
The polar angle of a, i.e. the angle a makes with the x-axis is φ.

Problem:

A vector A lies in the xy-plane.
(a) For what orientations of A will both of its rectangular components be negative?
(b) For what orientation will its components have opposite signs?

Solution:

Reasoning:
In a plane (in two dimensions), we can specify the direction of a vector by setting up a coordinate system and giving the angle φ the vector makes with the positive x-axis. A positive φ is an angle measured counterclockwise from the positive x-axis.
Details of the calculation:
(a) The x-component of A is A_x= A cosφ and the y-component of A is A_y= A sinφ. (A is the magnitude of the vector.) For A_x and A_y to be negative, we need cosφ and sinφ to be negative. φ must lie between 180 and 270 degrees.
(b) For A_x and A_y to have opposite signs, φ must lie between 90 and 180 degrees or between 270 and 360 degrees.

Note: The magnitude of a vector tells you how long it is. It is a number (with units). If the vector is a velocity vector, then its magnitude has units of speed (m/s), if it is a displacement vector, then its magnitude has units of distance (m), etc.
The direction in two dimensions, i.e. in a plane, is the angle the vector makes with the x-axis, measured counterclockwise from the x-direction.
You need a coordinate system (reference frame) before you specify the direction.

Adding vectors

To add physical vectors, they have to have the same units. To find the sum of two physical vector quantities with the same units algebraically, we add the x, y, and z-components of the individual vectors.

Example:

L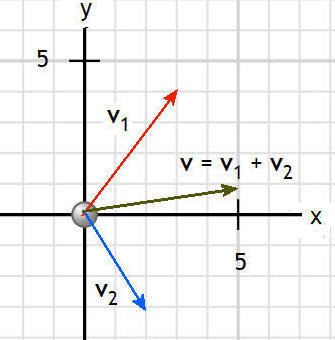et vector v₁ have components (3, 4) and vector v₂ have components (2, -3).
Let v = v₁ + v₂ be the sum of the two vectors.
Then the components of v are (3+2, 4+(-3) = (5, 1).
The magnitude of the vector v is v = (25 + 1)^½ = 5.1,
and the angle v makes with the x-axis is φ = tan^-1(1/5) = 0.197 rad = 11.3^o.

To subtract vector v₂ from vector v₁ we subtract the components of vector v₂ from the components of vector v₁.

Example:

Let vector v₁ have components (3, 4) and vector v₂ have components (2, -3).
Let v = v₁ - v₂ be the difference of the two vectors.
Then the components of v are (3-2, 4-(-3) = (1, 7).
The magnitude of the vector v is v = (1 + 49)^½ = 7.1
and the angle v makes with the x-axis is φ = tan^-1(7/1) = 1.429 rad = 81.9^o.

The graphical representation of a vector quantity is a directed line segment. To find the sum of two physical vector quantities with the same units graphically we line up the arrows, tail to tip. The sum is the arrow drawn from the tail of the first vector to the tip of the last vector. To subtract a vector v₂ from a vector v₁ we we invert vector v₂ and add it to vector v₁.

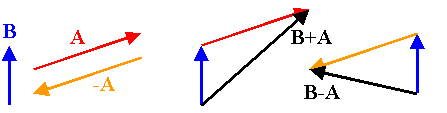
Let A be an arbitrary vector. The vector -A has the same length, and points in exactly the opposite direction. Subtracting the vector A from another vector means adding the vector -A to the other vector.

Example:

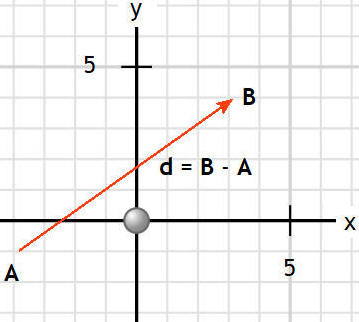The displacement vector
Let d represent the displacement vector from point A with coordinates (x₁, y₁) = (-4, -1) to point B with coordinates (x₂, y₂) = (3, 4).
The displacement vector is the difference between the position vectors A and B, d = B - A.

Its components are
d_x= (x₂ - x₁) = 3 - (-4) = 7, d_y= (y₂ - y₁) = 4 - (-1) = 5.
The displacement vector d has magnitude d = (49 + 25)^½ = 8.6.
The angle d makes with the x-axis is φ = tan^-1(5/7) = 0.62 rad = 35.5^o.

Summary:

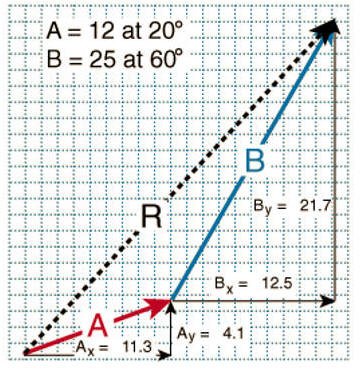Add two vectors A and B. R= A + B.

Find the x- and y-components of each vector.
A_x = 12 cos20^o = 11.3
A_y = 12 sin20^o = 4.1
B_x = 25 cos60^o = 12.5
B_y = 23 sin60^o = 21.7

Find the components of R.

R_x = A_x + B_x = 11.3 + 12.5 = 23.8
R_y = A_y + B_y = 4.1 + 21.7 = 25.8

Find the magnitude and direction of R.

R = (R_x² + R_y²)^½ = (23.8² + 25.8²)^½ = 35.1.
φ = tan^-1(R_y/R_x) = tan^-1(1.084) = 47.3^o.

External link: Lesson 1: Vectors - Fundamentals and Operations

Please study this material from "the Physics Classroom".