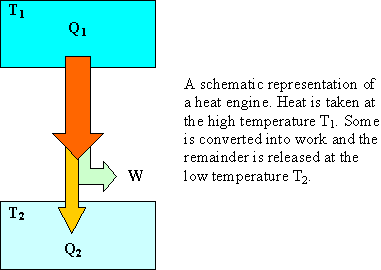To convert heat into work, you need at least two places with different temperatures.  If you take in Q_high at temperature T_high you must dump at least Q_low at temperature T_low.  The amount of work you get out of a heat engine is W = Q_high - Q_low.  The maximum amount of work you can get out of a heat engine is the amount you get out of a reversible engine.

W_max = (Q_high - Q_low)_reversible = Q_high - Q_highT_low/T_high = Q_high(1 - T_low/T_high).

W is positive if T_high is greater than T_low.

The efficiency of a heat engine is the ratio of the work obtained to the heat energy put in at the high temperature, e = W/Q_high.  The maximum possible efficiency e_max of such an engine is

e_max = W_max/Q_high = (1 - T_low /T_high) = (T_high - T_low)/T_high.

Steam engines

A steam engine is a type of heat engine.  It takes heat from the hot steam, converts some of this heat into useful work and dumps the rest into the colder surrounding air.  The maximum fraction of heat that can be converted into work can be found using the laws of thermodynamics, and it increases with the temperature difference between the hot steam and the surrounding air.  The hotter the steam and the colder the air, the more efficient is the steam engine at converting heat into work.

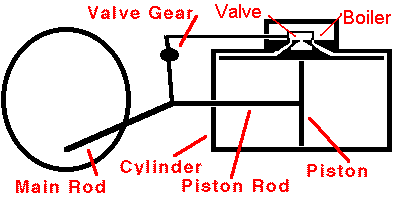
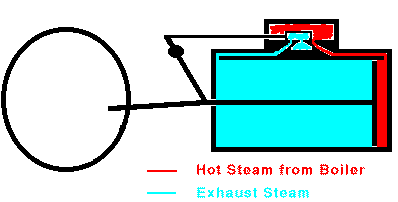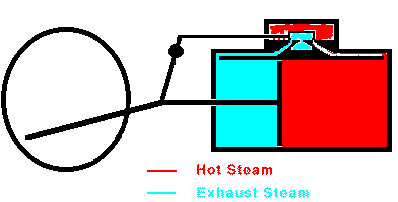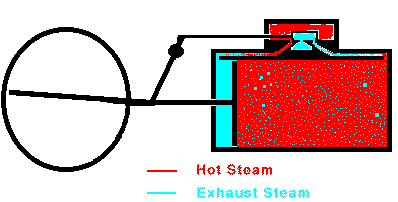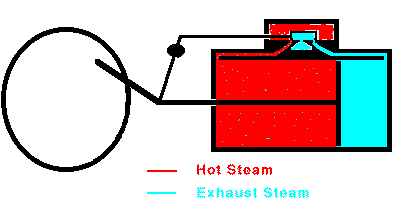
In a typical steam engine a piston moves back and forth inside a cylinder.  Hot, high-pressure steam is produced in a boiler, and this steam enters the cylinder through a valve.  Once inside the cylinder, the steam pushes outward on every surface, including the piston.  The piston moves.  The steam does mechanical work on the piston and the piston does mechanical work on the machinery attached to it.  The expanding steam transfers some of its thermal energy to this machinery, so the steam becomes cooler as the machinery operates.

When the piston reaches the end of its range, the valve stops the flow of steam and opens the cylinder to the outside air.  The piston can then return easily.  In many cases, steam is allowed to enter the other end of the cylinder so that the steam pushes the piston back to its original position.  Once the piston is back at its starting point, the valve again admits high-pressure steam to the cylinder and the whole cycle repeats.  Overall, heat is flowing from the hot boiler to the cooler surrounding air and some of that heat is being converted into mechanical work by the moving piston.  The maximum efficiency of a steam engine is e_max = (T_steam - T_air)/T_steam.  The actual efficiency is usually much lower.

External link:  Steam locomotive (Youtube)

Problem:

What is the maximum possible efficiency of a steam engine taking in heat at 100 ^oC and dumping it at room temperature of approximately 20 ^oC?

Solution:

• Reasoning:
  The maximum efficiency of any heat engine is that of a  Carnot engine.  e_max = (T_high - T_low)/T_high.
• Details of the calculation:
  100 ^oC = 373 K and  20 ^oC = 293 K.  The maximum possible efficiency is
  (T_high - T_low)/T_high =  (373 - 293)/373 = 0.21 = 21%.

Internal combustion engines

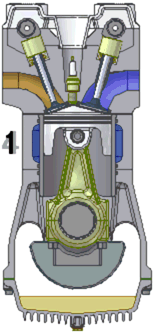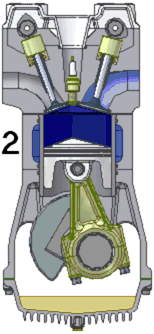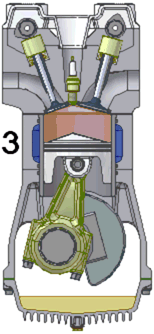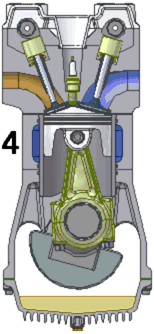
An internal combustion engine burns a mixture of fuel and air.  The most common type is a four-stroke engine.  A piston slides in and out of a cylinder.  Two or more valves allow the fuel and the air to enter the cylinder and the gases that form when the fuel and air burn to leave the cylinder.  As the piston slides back and forth inside the cylinder, the volume that the gases can occupy changes drastically.

The process of converting heat into work begins when the piston is pulled out of the cylinder, expanding the enclosed space and allowing fuel and air to flow into that space through a valve.  This motion is called the intake stroke or induction stroke.  Next, the fuel and the air mixture are squeezed together by pushing the piston into the cylinder.  This is called the compression stroke.  At the end of the compression stroke, with the fuel and the air mixture squeezed as tightly as possible, the spark plug at the sealed end of the cylinder fires and ignites the mixture.  The hot burning fuel has an enormous pressure and it pushes the piston out of the cylinder.  This power stroke is what provides power to the engine and the attached machinery.  Finally, the burned gas is squeezed out of the cylinder through another valve in the exhaust stroke.  These four strokes repeat over and over again.  Most internal combustion engines have at least four cylinders and pistons.  There is always at least one cylinder going through the power stroke and it can carry the other cylinders through the non-power strokes.  The maximum efficiency of such an engine is e_max = (T_ignition - T_air)/T_ignition where T_ignition is the temperature of the fuel-air mixture after ignition.  To maximize the fuel efficiency, you have to create the hottest possible fuel air mixture after ignition.  The highest efficiency that has been achieved is approximately 50% of e_max.

External link:  Internal combustion engine (Youtube)

Problem:

A heat engine absorbs 360 J of thermal energy and performs 25 J of work in each cycle.  Find
(a) the efficiency of the engine and
(b) the thermal energy expelled in each cycle.

Solution:

• Reasoning:
  The amount of work you get out of a heat engine is W = Q_high - Q_low.
  The efficiency is e = W/Q_high.
• Details of the calculation:
  Q_high = 360 J.  W = 25 J.  Q_low = Q_high - W = 335 J. 
  (a)  The efficiency e = W/Q_high = 6.9%.
  (b)  The thermal energy expelled is Q_low = 335 J.

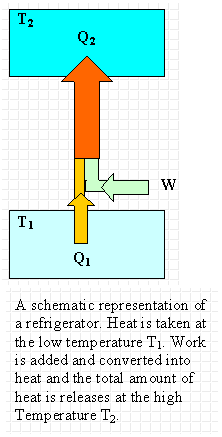Heat cannot, of itself, flow from a cold to a hot object is one way of stating the second law of thermodynamics.  If it could, then heat dumped at T_low could just flow back to the reservoir at T_high and the net effect would be an amount of heat ΔQ = Q_high - Q_low taken at a T_high and converted into work with no other changes in the system.

Assume you want to take heat from a place at T_low and dump it at a place with a higher temperature T_high.  You want to build a refrigerator or an air conditioner.  For such a device we define the coefficient of performance COP as the ratio of the amount of heat removed at the lower temperature to the work put into the system (i.e.  the engine).

COP = Q_low/(-W) = Q_low/(Q_high - Q_low).

The best possible coefficient of performance is

COP_max =  Q_low/(Q_high - Q_low)_max  = Q_low/(Q_low(T_high/T_low) - Q_low) = T_low/(T_high - T_low),

if we have a reversible engine moving the heat.  For a real engine Q_high is bigger than Q_lowT_high/T_low, and the coefficient of performance is smaller.

For a refrigerator keeping an inside temperature of 4 ^oC = 277 K operating in a room at 22 ^oC = 299 K the best possible coefficient of performance is COP_max = 277/(299 - 277) = 12.6.  The best possible ratio of the amount of heat removed to the work done is 12.6.  Heat cannot flow from inside an ordinary refrigerator into the warmer room unless we plug in the electric motor that does work on the refrigerant.

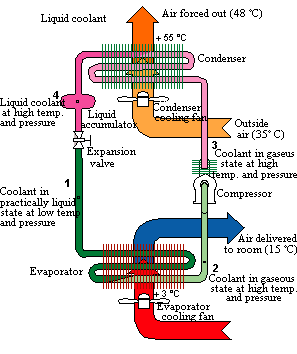An air conditioner is a refrigerator whose inside is the room to be cooled (T_room = T_low) and whose outside is the great outdoors (T_outside = T_high).  An air conditioner uses a material called a "working fluid" to transfer heat from inside of a room to the great outdoors.  The working fluid is a material which transforms easily from a gas to a liquid and vice versa over a wide range of temperatures and pressures.  This working fluid moves through the air conditioner's three main components, the compressor, the condenser, and the evaporator in a continuous cycle.

1. The working fluid enters the evaporator inside the room as a low-pressure liquid at approximately outside air temperature.
2. The evaporator is typically a snake-like pipe.  The fluid immediately begins to evaporate and expands into a gas.  In doing so, it uses its thermal energy to separate its molecules from one another and it becomes very cold.  Heat flows from the room into this cold gas.  The working fluid leaves the evaporator as a low-pressure gas a little below room temperature and heads off toward the compressor.
3. It enters the compressor as a low-pressure gas roughly at room temperature.  The compressor squeezes the molecules of that gas closer together, increasing the gas's density and pressure.  Since squeezing a gas involves physical work, the compressor transfers energy to the working fluid and that fluid becomes hotter.  The working fluid leaves the compressor as a high-pressure gas well above outside air temperature.
4. The working fluid then enters the condenser on the outside, which is typically a snake-like pipe.  Since the fluid is hotter than the surrounding air, heat flows out of the fluid and into the air.  The fluid then begins to condense into a liquid and it gives up additional thermal energy as it condenses.  This additional thermal energy also flows as heat into the outside air.  The working fluid leaves the condenser as a high-pressure liquid at roughly outside air temperature.  It then flows through a narrowing in the pipe into the evaporator.  When the fluid goes through the narrowing in the pipe, it's pressure drops and it enters the evaporator as a low-pressure liquid.  The cycle repeats.

Overall, heat is been extracted from the room and delivered to the outside air.  The compressor consumes electric energy during this process and that energy also becomes thermal energy in the outside air.  The maximum coefficient of such an air conditioner is COP_max = T_room/(T_outside - T_room).  Refrigerators and heat pumps work on the same principle.

A heat pump is a refrigerator whose inside is the great outdoors and whose outside is the room to be heated.  The coefficient of performance for a heat pump is the ratio of the energy delivered at the higher temperature to the work put into the system, COP = Q_high/(Q_high - Q_low).  The best possible coefficient of performance is

COP_max(heat pump) = (Q_high/(Q_high - Q_low))_max
= T_high/(T_high - T_low) = T_room/(T_room - T_outside)

If the outside temperature is 41 ^oF = 5^oC = 278 K and room temperature is 77^oF = 25^oC = 298K then COP_max = 298/(298 - 278) = 14.9.  However, if the outside temperature drops to 14 ^oF = -10 ^oC = 263 K then E_max = 298/(298 - 263) = 8.5.

Note: The coefficient of performance for a refrigerator/air conditioner and the coefficient of performance of a heat pump are defined differently.  We are always interested in how much work we have to do or how much useful energy we have to invest to accomplish something.  For a refrigerator or air conditioner we are interested in how efficiently heat is removed from the colder inside for a given amount of work done.  For a heat pump we are interested in how efficiently heat is delivered to the hotter inside for a given amount of work done.  The coefficient of performance gives us those ratios.

External link:  The refrigeration cycle (Youtube)

Problem:

What is the coefficient of performance of a refrigerator that operates with Carnot efficiency between temperatures of -3 ^oC and 27 ^oC?

Solution:

• Reasoning:
  For a refrigerator COP_max = T_low/(T_high - T_low).
• Details of the calculation:
  The best possible coefficient of performance is
  COP_max = T_low/(T_high - T_low) = 270/(300 - 270) = 9.

Problem:

A refrigerator has a coefficient of performance equal to 5.  If the refrigerator absorbs 120 J of thermal energy from a cold reservoir in each cycle, find
(a) the work done in each cycle and
(b) the thermal energy expelled to the hot reservoir. 

Solution:

• Reasoning:
  For a refrigerator the coefficient of performance is COP = Q_low/(-W).
• Details of the calculation:
  (a)  COP = Q_low/(-W).  (-W) = Q_low/COP = 120/5 J = 24 J.
  The work is done on the system.  Ordered (electrical) energy is converted into thermal energy.
  (b)  (-W) = 24 J = Q_high - Q_low.  Q_high = 24 J + 120 J = 144 J.

Embedded Question 2

The energy output of a heat pump is greater than the energy used to operate the pump.  Why doesn't this statement violate the first law of thermodynamics?

Discuss this with your fellow students in the discussion forum!