An example of an idealized, frictionless engine in which all the processes are reversible is an ideal gas in a cylinder equipped with a frictionless piston. The cylinder alternates in making contact with one of two heat reservoirs at temperatures T1 and T2 respectively, with T1 higher than T2.
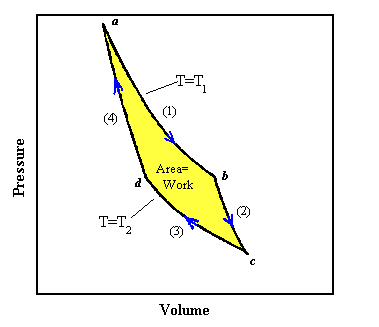
(1) We start at point a in the PV diagram. Let us put the cylinder in contact with the reservoir at T1 and heat the gas and at the same time expand it following the curve marked (1). To make the process reversible we pull the piston out very slowly as heat flows into the gas and we make sure that the temperature of the gas stays nearly equal to T1. If we would push the piston back in slowly, then the temperature would only be infinitesimally higher than T1 and the heat would flow back from the gas into the reservoir. An isothermal expansion, when done slowly enough, can be a reversible process. The curve marked (1) from point a to point b tells us how the pressure and volume change if the temperature is kept fixed at the value T1. For an ideal gas this curve is given by PV = NkT1. As the volume increases, the pressure drops. Once we reach point b in the diagram an amount of heat Q1 has been transferred from the reservoir into the gas. Since the expansion is isothermal, the temperature of the gas has not changed, ΔU = 0 and ΔQ1 = ΔW.
ΔQ1 = ΔW = ∫ab PdV = ∫ab (NkBT1/V) dV = NkBT1 ln(Vb/Va).
ΔQ1 = Q1 is positive, heat flows into the gas in the
cylinder.
(2) Let us take the cylinder away from the reservoir at point b and continue a slow,
reversible expansion without permitting heat to enter the cylinder. The expansion now is
adiabatic. As the gas expands the temperature falls, since there is no heat entering the cylinder. We
let the gas expand, following the curve marked (2), until the temperature falls to T2
at the point marked c. The adiabatic curve has a more negative slope than the
isothermal curve. For the adiabatic expansion of an ideal gas made from point particles,
we have ΔU = -ΔW since ΔQ = 0. Therefore
dU = -dW = -PdV.
But we also have
U = N½m<v2>,
since the internal energy is the random kinetic energy of the gas atoms. Using, from the kinetic theory, PV = (2/3)N½m<v2> we have
U = (3/2)PV.
Then, from calculus, we have
dU = (3/2)(PdV + VdP).
Equating our two expressions for dU we have
-PdV = (3/2)(PdV + VdP),
(-5/2)PdV = (3/2)VdP,
dP/P + (5/3)dV/V = 0.
We can integrate to obtain lnP + (5/3)lnV = lnC, where lnC is the constant of integration. This yields
PV5/3 = C = constant
for an adiabatic expansion of an ideal gas. Since PV = NkT we can write PV5/3 = NkTV2/3 = C, or TV2/3 = constant. Therefore
T1Vb2/3 = T2Vc2/3 or Vb/Vc = (T2/T1)-2/3.
(3) When the gas has reached the temperature T2 we put it in contact with the reservoir at T2. Now we slowly compress the gas isothermally while it is in contact with the reservoir at T2, following the curve marked (3). The temperature of the gas does not rise and an amount of heat ΔQ2 flows from the cylinder into the reservoir at the temperature T2. For the isothermal process we have
ΔQ2 = ΔW = ∫cd PdV = ∫cd (NkBT2/V) dV = NkBT2 ln(Vd/Vc).
ΔQ2 = -Q2 is negative, heat is removed from the gas in
the cylinder.
(4) At the point d we remove the cylinder from the reservoir at T2 and
compress it still further, without letting any heat flow out. During this
adiabatic process the temperature rises, and the pressure follows the curve marked (4). If we carry
out each step properly, we can return to the point a at temperature T1
where we started, and repeat the cycle. For the adiabatic process from point d to point a we have
T2Vd2/3 = T1Va2/3 or Va/Vd = (T2/T1)-2/3.
Therefore
Va/Vd = Vb/Vc, Vb/Va = Vc/Vd, and ln(Vb/Va)= ln(Vc/Vd) = -ln(Vd/Vc).
In going from point a to point c, the gas expands and does work. In going from point c back to point a work is done on the gas. The work done is always the area under the curve in the PV diagram. The net amount of work done by the gas is the yellow area of the figure. Because everything we have done is reversible, we could also have gone backwards instead of forwards through the cycle. Then the area under the curve would represent the net amount of work done on the gas.
During one cycle we have put an amount of heat Q1 into the gas at temperature T1 and have removed an amount of heat Q2 at temperature T2. From the above equations we see that
Q1/Q2 = (T1 ln(Vb/Va))/(T2 ln(Vd/Vc))
= T1/T2, or
Q1/T1
= Q2/T2.
We have shown that if our ideal reversible engine picks up the amount of heat Q1 from a reservoir at temperature T1 and delivers the amount of heat Q2 to a reservoir at temperature T2, then Q1/T1 = Q2/T2. The work done by the engine on its surroundings is W = Q1 - Q2 = Q1 (1 - T2 / T1).