Often the system from which we want to extract heat to do work is a gas.  When a gas expands, how much work does it do on its surroundings?

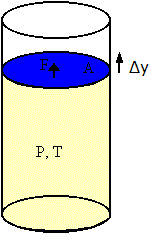
Consider an ideal gas in a cylinder with a movable piston.  The gas occupies a volume V, the temperature is T, and the pressure is P.  Assume that the piston has a cross-sectional area A.  Assume the gas expands by a small amount and the piston moves out by a small amount Δy.  The gas exerts a force F = PA on the piston and therefore does work ΔW = FΔy on the piston.

ΔW = FΔy = PAΔy = PΔV

ΔV is the change in volume of the gas.  ΔV is positive because the gas expands.  (If the gas is being compresses, then ΔV is negative and work is done on the gas.)

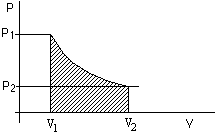If the volume of the gas changes from V₁ to V₂, then the total work done by the gas depends on how exactly the pressure varies during the expansion process. 
W = ∑_jP_jΔV_j.  We sum the work done during a large number of small changes of the volume.

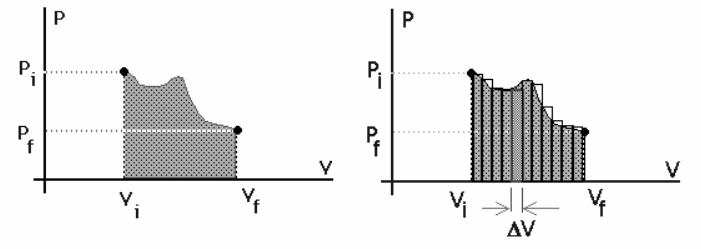
If the pressure and volume are known at each step of the expansion process, then the work can be represented as the area under the curve on a PV diagram.

• An adiabatic process is a process during which no heat enters or leaves the system.
  We then have ΔU = -ΔW, i.e. ΔW equals the change in a physical property of the system.
  A physical property of the system depends only on the state of the system (P, V, T), not on the way the system was put into this state.
  In practice there are two different ways to prevent the transfer of heat.
  (a)  Provide very good thermal insulation of the system.
  (b)  Complete the process in a very short time interval, so that there is no time for appreciable heat transfer.  The combustion process inside a car engine is essentially adiabatic for this reason.
• An isobaric process is a process that occurs at constant pressure.
  We then have W = P(V₂ - V₁).
  If the pressure of an ideal gas is kept constant, then the temperature must increase as the gas expands.  (PV/T = constant.)  Heat must be added during the expansion process.
  We define the enthalpy H of the system by the equation H = U + PV.
  The enthalpy is a physical property of the system.  It depends only on the state of the system (internal energy, pressure, volume), not on how it reached this state.  Enthalpy has the dimensions of energy and the SI unit of enthalpy is Joule. 
  For an isobaric process we write ΔU = ΔQ - ΔW = ΔQ - P(V₂ - V₁), or, rearranging the terms, ΔH = ΔQ.
  This expression, often used in chemistry, can be regarded as the isobaric form of the first law.
  ΔH = ΔQ only holds for isobaric processes.  Chemical reactions (including biological ones) often take place at constant pressure, and then ΔQ is equal to the change in a physical property of the system.
• An isovolumetric or isometric process takes place at constant volume.
  Then W = 0 and ΔU = ΔQ.
  All the heat added to the system goes into increasing its internal energy.
• An isothermal process occurs at constant temperature.
  Since the internal energy of a gas is only a function of its temperature, ΔU = 0 for an isothermal process.
  For the isothermal expansion of an ideal gas we have W = nRT ln(V₂/V₁).
  W is positive if V₂ > V₁.  Since ΔU = 0, the heat transferred to the gas is ΔQ = W.

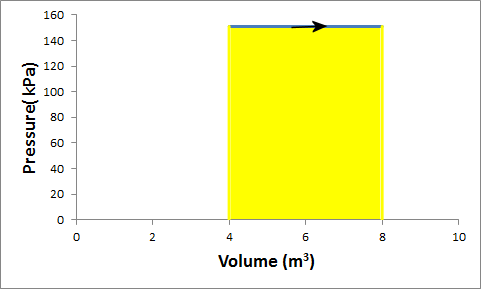Problem:

Solution:

• Reasoning:
  The process is isobaric.  For an isobaric process W = P(V₂ - V₁).
• Details of the calculation:
  W = P(V₂ - V₁) = P(2V₁ - V₁) = PV₁ = 151500 Pa*4 m³ = 606000 J.
  (The work is the area under curve in the PV diagram.  ΔV is positive because the gas expands, and therefore the work W done by the gas is positive.)

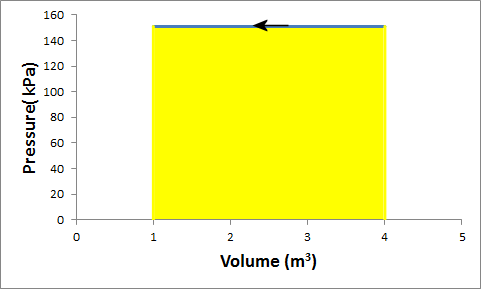Problem:

G in a container is at a pressure of 1.5 atm and a volume of 4 m³.  What is the work done by the gas if it is compressed at constant pressure to 1/4 of its initial volume?

Solution:

• Reasoning:
  The process is isobaric.  For an isobaric process W = P(V₂ - V₁).
• Details of the calculation:
  W = P(0.25V₁ - V₁) = -0.75 PV₁ = -454500 J.
  (The work is the area under curve in the PV diagram.  ΔV is negative because the gas is compressed, and therefore the work W done by the gas is negative.)

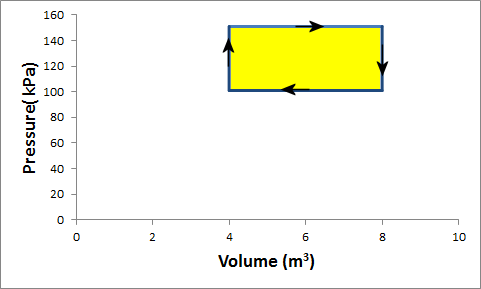Problem:

Gas in a container is at a pressure of 1.5 atm and a volume of 4 m³.  What is the net work done by the gas if it goes through the following cycle?

(i)  The gas expands at constant pressure of 1.5 atm to a volume of 4 m³.
(ii)  At constant volume of 4 m³ the pressure is reduced to 1 atm.
(iii)  The gas is compressed at constant pressure of 1 atm to a volume of 4 m³.
(iv)  At constant volume of 4 m³ the pressure is increased to 1.5 atm.

Solution:

• Reasoning:
  Processes (i) and (iii) are isobaric.  W = PΔV.
  Processes (i) and (iii) are isometric.  W = 0.
• Details of the calculation:
  (i)  W = PΔV = 151500 Pa*4 m³ = 606000 J.
  (ii)  W = 0 since ΔV = 0. (no displacement <--> no work).
  (iii)  W = PΔV = -101000 Pa*4 m³ = -404000 J.
  (iv)  W = 0.
  Net work done by the gas:  W_net = 606000 J - 404000 J = 202000 J.

The net work done by the gas in one cycle of a process that returns the gas to its initial condition is the area inside the closed loop in the PV diagram.  If the loop is traversed in a clockwise direction the net work is positive.  If the loop is traversed in a counterclockwise direction the net work is negative.

• When a gas expands it does positive work. It pushes against the wall of the container and the wall of the container move outward.  We have ∆W = F*∆r = (F/A)*A*∆r = P *∆V.  Here A is the area of the container wall that has moved and ∆r is how much it has moved outward.
• When the volume of the gas decreases, the gas does negative work. ∆W = -P*∆V. The gas still pushes outward against the wall, but the wall moves inward.
• When the volume does not change, the gas does no work, no matter the value of the pressure.
• So when you have a P-V diagram (P vertical axis, V horizontal axis) showing a closed loop, you can break up the loop into small steps that either increase or decrease the volume or do not change it.
  Any positive ∆V (towards greater V) implies the gas does positive work P*∆V, and any negative ∆V (towards smaller V) implies the gas does negative work -P*∆V.
• Adding it all up you find that the work done by the gas is the area inside the loop in the P-V diagram. The work is positive if the pressure is higher during the expansion than during the contraction, and the work is negative (work is done on the gas) it the pressure is lower during the expansion than during the contraction.

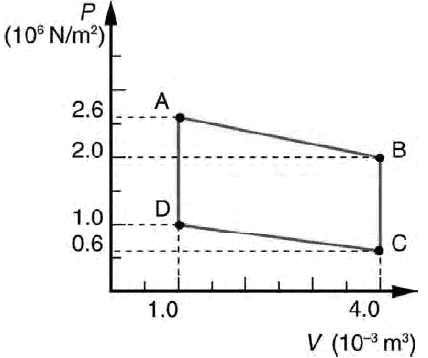
Problem:

Calculate the net work output of a heat engine following path ABCDA in the figure on the right.

Solution:

• Reasoning:
  The path is a closed loop in the PV diagram.
  The net work done is the area inside the closed loop in the PV diagram.
• Details of the calculation:
  W =  (1.5 * 3)*(10⁶ N/m²)(10^-3 m³) = 4.5*10³ J,
  using area = average height * width.
  or
  area inside the loop = area of center rectangle + area of top triangle - area of bottom triangle
  = (1*3 + 0.6*3/2 - 0.4*3/2)*(10⁶ N/m²)(10^-3 m³) =  4.5*10³ J.

Problem:

A gas is compressed at a constant pressure of 0.8 atm from 9 liter to 2 liter.  (1 liter = 10^-3 m³)  In the process, 400 J of thermal energy leaves the gas.
(a) What is the work done by the gas?
(b) What is the change in its internal energy?

Solution:

• Reasoning:
  For an isobaric process W = P(V₂ - V₁).
  Energy conservation:  ΔU = ΔQ - ΔW.
• Details of the calculation:
  (a)  W = P(V₂ - V₁) = -80800 Pa*7*10^-3 m³ = -565.6 J . (Work is done on the gas.)
  (b)  ΔU = -400 J + 565.6 J = 165.6 J.

Problem:

One mole of an ideal gas does 3000 J of work on its surroundings as it expands isothermally to a final pressure of 1 atm and volume of 25 L.  Determine
(a)  the initial volume and
(b)  the temperature of the gas.

Solution:

• Reasoning:
  For an isothermal process the temperature is constant.
  Therefore PV = nRT = constant.  Here n = 1.
  Since the final pressure and volume are given, we know nRT.
  W = nRT ln(V₂/V₁) for an isothermal process.
  Since W is given, we can solve for V₁.
• Details of the calculation:
  (a)  PV = 101000 Pa*25*10^-3 m³ = nRT.
  W = nRT ln(V₂/V₁) for an isothermal process.
  W/(nRT) = ln(V₂/V₁) = 3000 J/(101000 Pa*25*10^-3 m³) = 1.19.
  V₂/V₁ = exp(1.19) = 3.28.
  V₁ = (25*10^-3 m³)/3.28 = 7.62*10^-3 m³ = 7.62 liter.
  
  (b)  For an ideal gas PV = nRT.  101000Pa*25*10^-3 m³ = (8.31 J/K)T.  T = 303.85 K.

A bicycle ergometer is an apparatus that resembles a bicycle and is used to measure the amount of work done by a person while pedaling to rotate a large flywheel, usually the front wheel of a stationary bicycle, against a frictional force.  The work done to overcome the frictional force is converted into thermal energy, which causes the temperature of the flywheel and of other components in contact with the system to increase.  A nylon belt, which is under tension and wound around the wheel, can provide the frictional force.  The tension can be measured with a calibrated spring.  The work W done by the person on the ergometer is the product of the force due to the tension F in the belt times the distance through which this force acts.  The force is tangential to the rim of the wheel.  The distance is therefore 2π times the radius of the flywheel r times the number of revolution N made by the wheel.  We have W = NF2πr.  For the ergometer we have from the first law of thermodynamics ΔU = ΔQ - ΔW.  ΔW is positive if the system does work on its surroundings and is negative if work is done on the system.  Here ΔW is negative, since the person does work on the ergometer.  ΔW = -W.  ΔQ is the heat put into or taken out of the system.  We have ΔU - ΔQ = NF2πr.  If we neglect the heat lost by the system to its surroundings and set ΔQ = 0, then the increase in the thermal energy of the system equals ΔU = NF2πr.  The temperature of the flywheel therefore increases by ΔT = ΔU/mc, where m is the mass of the flywheel and c is its specific heat capacity. 
The ergometer converts useful work into thermal energy.  By analyzing the air exhaled by the person pedaling the ergometer, the rate at which the body uses chemical energy can be measured.  By knowing how much chemical energy the body uses at rest and how much it uses while pedaling, the efficiency of the body in converting chemical energy into useful work can be determined.

Embedded Question 1

There is no change in the internal energy of an ideal gas undergoing an isothermal process since the internal energy depends only on the temperature.  Is it therefore correct to say that an isothermal process is the same as an adiabatic process for an ideal gas?  Explain your answer.

Discuss this with your fellow students in the discussion forum!