An object moving along the x-axis is said to exhibit simple harmonic motion if its position as a function of time varies as

x(t) = x₀ + A cos(ωt + φ).

The object oscillates about the equilibrium position x₀.  If we choose the origin of our coordinate system such that x₀ = 0, then the displacement x from the equilibrium position as a function of time is given by

x(t) = A cos(ωt + φ).

A is the amplitude of the oscillation, i.e. the maximum displacement of the object from equilibrium, either in the positive or negative x-direction.  Simple harmonic motion is repetitive.  The period T is the time it takes the object to complete one oscillation and return to the starting position.  The angular frequency ω is given by ω = 2π/T.  The angular frequency is measured in radians per second.  The inverse of the period is the frequency f = 1/T.  The frequency f = 1/T = ω/2π of the motion gives the number of complete oscillations per unit time.  It is measured in units of Hertz, (1 Hz = 1/s).

The velocity of the object as a function of time is given by

v(t) = -ω A sin(ωt + φ),

and the acceleration is given by

a(t) = -ω²A cos(ωt + φ) = -ω²x.

The quantity φ is called the phase constant.  It is determined by the initial conditions of the motion.  If at t = 0 the object has its maximum displacement in the positive x-direction, then φ = 0, if it has its maximum displacement in the negative x-direction, then φ = π.  If at t = 0 the particle is moving through its equilibrium position with maximum velocity in the negative x-direction then φ = π/2.  The quantity ωt + φ is called the phase.

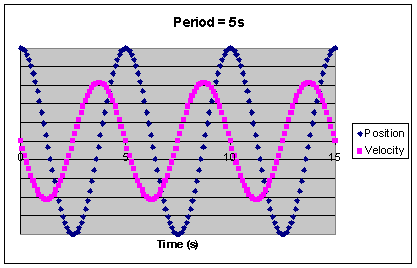
In the figure below position and velocity are plotted as a function of time for oscillatory motion with a period of 5 s.  The amplitude and the maximum velocity have arbitrary units.  Position and velocity are out of phase.  The velocity is zero at maximum displacement, and the displacement is zero at maximum speed.

For simple harmonic motion, the acceleration a = -ω²x is proportional to the displacement, but in the opposite direction.  Simple harmonic motion is accelerated motion.  If an object exhibits simple harmonic motion, a force must be acting on the object.  The force is

F = ma = -mω²x.

It obeys Hooke's law, F = -kx, with k = mω².

External link:  Simple harmonic motion  (Youtube)

The force exerted by a spring obeys Hooke's law.  Assume that an object is attached to a spring, which is stretched or compressed.  Then the spring exerts a force on the object.  This force is proportional to the displacement x of the spring from its equilibrium position and is in a direction opposite to the displacement.

F = -kx

Assume the spring is stretched a distance A from its equilibrium position and then released.  The object attached to the spring accelerates as it moves back towards the equilibrium position.

a = -(k/m)x

It gains speed as it moves towards the equilibrium position because its acceleration is in the direction of its velocity.  When it is at the equilibrium position, the acceleration is zero, but the object has maximum speed.  It overshoots the equilibrium position and starts slowing down, because the acceleration is now in a direction opposite to the direction of its velocity.  Neglecting friction, it comes to a stop when the spring is compressed by a distance A and then accelerates back towards the equilibrium position.  It again overshoots and comes to a stop at the initial position when the spring is stretched a distance A.  The motion repeats.  The object oscillates back and forth.  It executes simple harmonic motion.  The angular frequency of the motion is

ω = √(k/m),

the period is

T = 2π√(m/k),

and the frequency is

f = (1/(2π))√(k/m).

Problem:

A particle oscillates with simple harmonic motion, so that its displacement varies according to the expression x = (5 cm)cos(2t + π/6) where x is in centimeters and t is in seconds.  At t = 0 find
(a)  the displacement of the particle,
(b)  its velocity, and
(c)  its acceleration.
(d)  Find the period and amplitude of the motion.

Solution:

• Reasoning:
  Analyze simple harmonic motion.
  x(t) = A cos(ωt + φ).  A = amplitude, ω = angular frequency,  φ = phase constant.
  v(t) = -ω A sin(ωt + φ),  a(t) = -ω²A cos(ωt + φ) = -ω²x.
• Details of the calculation:
  (a)  The displacement as a function of time is x(t) = Acos(ωt + φ).  Here ω = 2/s, φ = π/6, and A = 5 cm. 
  The displacement at t = 0 is x(0) = (5 cm)cos(π/6) = 4.33 cm.
  (b)  The velocity at t = 0 is v(0) = -ω(5 cm)sin(π/6) = -5 cm/s.
  (c)  The acceleration at t = 0 is a(0) = -ω²(5 cm)cos(π/6) = -17.3 cm/s².
  (d)  The period of the motion is T = 2π/ω = π s, and the amplitude is 5 cm.

Problem:

A 20 g particle moves in simple harmonic motion with a frequency of 3 oscillations per second and an amplitude of 5 cm.
(a)  Through what total distance does the particle move during one cycle of its motion?
(b)  What is its maximum speed?  Where does that occur?
(c)  Find the maximum acceleration of the particle.  Where in the motion does the maximum acceleration occur?

Solution:

• Reasoning:
  Analyze simple harmonic motion, x(t) = A cos(ωt + φ).
• Details of the calculation:
  (a)  The total distance d the particle moves during one cycle is from x = -A to x = +A and back to x = -A, so d = 4A = 20 cm.
  (b)  The maximum speed of the particle is
  v_max = ωA = 2πfA = 2π 15 cm/s = 0.94 m/s.
  The particle has maximum speed when it passes through the equilibrium position.
  (c) The maximum acceleration of the particle is
  a_max = ω²A = (2πf)²A = 17.8 m/s².
  The particle has maximum acceleration at the turning points, where it has maximum displacement.

Assume a mass suspended from a vertical spring of spring constant k.  In equilibrium the spring is stretched a distance x₀ = mg/k.  If the mass is displaced from equilibrium position downward and the spring is stretched an additional distance x, then the total force on the mass is mg - k(x₀ + x) = -kx directed towards the equilibrium position.  If the mass is displaced upward by a distance x, then the total force on the mass is mg - k(x₀ - x) = kx, directed towards the equilibrium position.  The mass will execute simple harmonic motion.  The angular frequency ω = SQRT(k/m) is the same for the mass oscillating on the spring in a vertical or horizontal position.  But the equilibrium length of the spring about which it oscillates is different for the vertical position and the horizontal position.

Assume an object attached to a spring exhibits simple harmonic motion.  Let one end of the spring be attached to a wall and let the object move horizontally on a frictionless table.

What is the total energy of the object?

The object's kinetic energy is

K = ½mv² = ½mω²A²sin²(ωt + φ).

Its potential energy is elastic potential energy.  The elastic potential energy stored in a spring displaced a distance x from its equilibrium position is U = ½kx².  The object's potential energy therefore is

U = ½kx² = ½mω²x² = ½mω²A²cos²(ωt + φ).

The total mechanical energy of the object is

E = K + U = ½mω²A²(sin²(ωt + φ) + cos²(ωt + φ)) = ½mω²A².

The energy E in the system is proportional to the square of the amplitude.

E = ½kA².

It is a continuously changing mixture of kinetic energy and potential energy.

For any object executing simple harmonic motion with angular frequency ω, the restoring force F = -mω²x obeys Hooke's law, and therefore is a conservative force.  We can define a potential energy U = ½mω²x², and the total energy of the object is given by E = ½mω²A².  Since v_max = ωA, we can also write E = ½mv_max².

Problem:

A particle that hangs from a spring oscillates with an angular frequency of 2 rad/s.  The spring is suspended from the ceiling of an elevator car and hangs motionless (relative to the car) as the car descends at a constant speed of 1.5 m/s.  The car then suddenly stops.  Neglect the mass of the spring.
With what amplitude does the particle oscillate?

Solution:

• Reasoning:
  When traveling in the elevator at constant speed, the total force on the mass is zero.  The force exerted by the spring is equal in magnitude to the gravitational force on the mass, the spring has the equilibrium length of a vertical spring.  When the elevator suddenly stops, the end of the spring attached to the ceiling stops.  The mass, however has momentum, p = mv, and therefore starts stretching the spring.  It moves through the equilibrium position of the vertical spring with its maximum velocity v_max = 1.5 m/s.
  Its velocity as a function of time is v(t) = -ωAsin(ωt + φ).
• Details of the calculation:
  Since v_max = ωA and ω = 2/s, the amplitude of the amplitude of the oscillations is A = 0.75 m.

Problem:

A mass-spring system oscillates with an amplitude of 3.5 cm.  If the force constant of the spring of 250 N/m and the mass is 0.5 kg, determine
(a)  the mechanical energy of the system,
(b)  the maximum speed of the mass, and
(c)  the maximum acceleration.

Solution:

• Reasoning:
  The mechanical energy of a system executing simple harmonic motion is E = ½kA² = ½mω²A².
• Details of the calculation:
  (a)  We have m = 0.5 kg, A = 0.035 m, k = 250 N/m, ω² = k/m = 500/s², ω = 22.36/s.
  The mechanical energy of the system is E = ½kA² = 0.153 J.
  (b)  The maximum speed of the mass is v_max = ωA = 0.78 m/s.
  (c)  The maximum acceleration is a_max = ω²A = 17.5 m/s².