 Vibrating objects can produce sound. The vibrating object can be a string,
an air column, a membrane, etc. When the object moves outward, it pushes the
air molecules, creating a region of high pressure. When it moves inward it
creates a region of low pressure. As the vibrating object alternately
compresses and expands the surrounding air, the disturbance travels
outward from the source as a longitudinal wave.
Vibrating objects can produce sound. The vibrating object can be a string,
an air column, a membrane, etc. When the object moves outward, it pushes the
air molecules, creating a region of high pressure. When it moves inward it
creates a region of low pressure. As the vibrating object alternately
compresses and expands the surrounding air, the disturbance travels
outward from the source as a longitudinal wave.
Sound waves can be produced in a column of air and
travel along a pipe in only one dimension. But the sound
produced by most sources travels in three dimensions. The energy E
carried by the sound wave spreads out over an area that increases
proportional to the square of the distance from the source. The
intensity I or energy per unit area therefore must be inverse
proportional to the square of the distance from the source.
I is proportional to 1/r2
Since I is also proportional to the square of the amplitude of the wave,
we have A2 is proportional to 1/r2, or A is
proportional to 1/r. In three dimensions, the amplitude of an undamped wave is not constant, but decreases as 1/r, where r is the
distance from the source. With damping, it decreases with distance
from the source faster than 1/r.
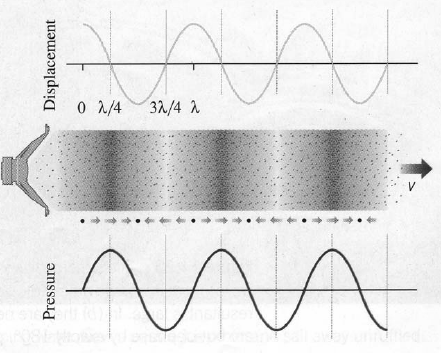 The pressure variations ∆P of a sound wave are
usually much smaller than the equilibrium pressure P. For a traveling sound wave in one-dimension we have for
the pressure variations ∆P from equilibrium pressure
The pressure variations ∆P of a sound wave are
usually much smaller than the equilibrium pressure P. For a traveling sound wave in one-dimension we have for
the pressure variations ∆P from equilibrium pressure
∆P(x,t) = ∆Pmaxsin(kx - ωt + φ).
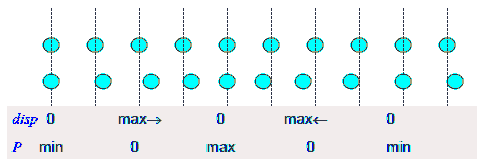 The displacements of the air molecules from their
equilibrium positions are out of phase with the pressure variation by
π/2. We therefore have for the displacements ∆s
from the equilibrium position
The displacements of the air molecules from their
equilibrium positions are out of phase with the pressure variation by
π/2. We therefore have for the displacements ∆s
from the equilibrium position
∆s(x,t) = ∆smaxcos(kx - ωt + φ).
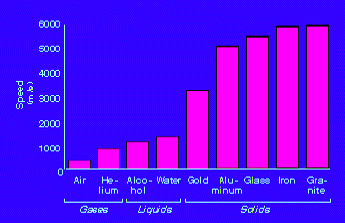 The speed of sound at standard
temperature and pressure (25 oC, 760 mm of mercury) is 343 m/s (767
miles/h). It is determined by how often the air molecules collide. The speed
of sound increases by about 6 m/s if the temperature increases by 10 oC.
Sound travels faster in liquids and solids than in gases, since the particles in
liquids and solids are closer together and can respond more quickly to the
motion of their neighbors. The speed of sound in water is ~1500 m/s, in iron it
is ~5000 m/s.
The speed of sound at standard
temperature and pressure (25 oC, 760 mm of mercury) is 343 m/s (767
miles/h). It is determined by how often the air molecules collide. The speed
of sound increases by about 6 m/s if the temperature increases by 10 oC.
Sound travels faster in liquids and solids than in gases, since the particles in
liquids and solids are closer together and can respond more quickly to the
motion of their neighbors. The speed of sound in water is ~1500 m/s, in iron it
is ~5000 m/s.
The speed of a sound wave through a medium does NOT depend
on the frequency of the wave.
External link: Speed of sound in various media
Problem:
Middle C on the musical scale has a frequency of 262 Hz. What is the
wavelength of the sound wave?
Solution:
- Reasoning:
For all periodic waves v = λf. The speed of sound in air is
approximately v = 340 m/s.
- Details of the calculation:
λ = v/f = (340 m/s)/(262/s) = 1.30 m.
Problem:
What is the speed of sound in a medium where a 100 kHz frequency produces a
5.96 cm wavelength?
Solution:
- Reasoning:
For all periodic waves v = λf.
- Details of the calculation:
v = λf = (5.96 *10-2 m)*105/s = 5.96*103
m/s.
This is the speed of sound in steel.
Our ears are most sensitive to sounds in the frequency range of 3000 Hz -
4000 Hz. Almost nobody hears sounds outside the range of 20 Hz - 20000 Hz.
Sound waves whose frequencies are less than 20 Hz are called
infrasonic waves and sound waves whose
frequencies are higher than 20000 Hz are called ultrasonic waves.
The energy carried by a sound wave is proportional to the square of its
amplitude. The energy passing a unit area per unit time is called the
intensity of the wave. The higher the
intensity, the louder is the sound. Our ears, however, do not respond linearly
to the intensity. A wave that carries twice the energy does not sound twice as
loud. Sound levels β are measured using a logarithmic scale.
β = 10 log10(I/I0)
The units of β are decibels (dB). I0 = 10-12 W/m2 is the reference intensity.
Problem:
What is the decibel level of a sound that is 10 times as intense as a
90.0 dB sound?
Solution:
- Reasoning:
Sound levels are measured in decibel. β(dB) = 10 log10(I/I0).
- Details of the calculation:
Let β0 = 10 log10(I/I0)
= 90 dB.
Math:
log10(10*x)
= log10(10)
+ log10(x)
= 1 + log10(x).
log10(10*I/I0) = log10(10) +
log10(I/I0) = 1 + log10(I/I0).
β = 10 log10(10*I/I0)
= 10 + 10 log10(I/I0)
= 10 + β0 = 100 dB.
MULTIPLY the intensity by 10 < = > ADD another 10 dB to the sound level
Problem:
What is the intensity of a sound that is 3.00 dB higher than a
4*10-9 W/m2 sound?
Solution:
- Reasoning:
Sound levels are measured in decibel. β(dB) = 10 log10(I/I0).
- Details of the calculation:
β2 - β1 = 10 log10(I2/I1)
= 3. I2/I1 = 100.3 = 2.
I2 = 8*10-9 W/m2.
MULTIPLY the intensity by 2 < = > ADD another 3 dB to the sound level
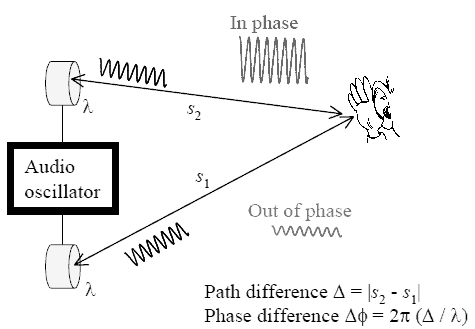 Like all waves, two or more sound waves traveling through the same medium will
interfere. We can have constructive and destructive interference. If a person
stands equidistant from two speakers which are playing the same sound in phase,
i.e. which are moving in and out together, then the two waves arrive in phase
after traveling the same distance. Crest meets crest and trough meets trough at
the location of the person. The amplitudes of the two waves add and the sound
is loudest here. If the two speakers play the same sound but are out of phase,
i.e. one is moving out while the other is moving in, then the sound has a low
volume at the location of the person equidistant from the two speakers. This
can easily be demonstrated by switching the wires on one of the speakers. (This
is why you need to pay attention to the color of the wires when setting up your
stereo). Dead spots in an auditorium are sometimes produced by destructive
interference.
Like all waves, two or more sound waves traveling through the same medium will
interfere. We can have constructive and destructive interference. If a person
stands equidistant from two speakers which are playing the same sound in phase,
i.e. which are moving in and out together, then the two waves arrive in phase
after traveling the same distance. Crest meets crest and trough meets trough at
the location of the person. The amplitudes of the two waves add and the sound
is loudest here. If the two speakers play the same sound but are out of phase,
i.e. one is moving out while the other is moving in, then the sound has a low
volume at the location of the person equidistant from the two speakers. This
can easily be demonstrated by switching the wires on one of the speakers. (This
is why you need to pay attention to the color of the wires when setting up your
stereo). Dead spots in an auditorium are sometimes produced by destructive
interference.
Problem:
In a situation as shown in the figure above, let ∆ = 1 m and the speed of sound be
340 m/s. Sound at
which of the following frequencies will be loud at the position of the
listener?
1. f = 680 Hz
2. f = 1190 Hz
3. f = 340 Hz
Solution:
- Reasoning:
Constructive interference: λ = ∆/m, f = v/λ = mv/∆.
Destructive interference: λ = ∆/(m + ½), f = v/λ = (m + ½)v/∆.
- Details of the calculation:
Here ∆ = 1 m.
If f*∆/v is an integer, we have constructive interference, if it is an integer plus ½, we have destructive interference.
Case 1: f = 680 Hz, f*∆/v = 680/340 = 2.
Case 2: f = 1190 Hz, f*∆/v = 1190/340 = 3.5.
Case 3: f = 340 Hz, f*∆/v = 340/340 = 1.
For f = 680 Hz and f = 340 Hz we have
constructive interference and the sound will be loud.
External link: The Physics
Classroom: Sound Waves and Music (Lessons 1 and 2)
Embedded Question 1
Speakers in stereo systems have two color-coded terminals to indicate how to
hook up the wires. If the wires are reversed, the speaker moves in a
direction opposite that of a properly connected speaker. Explain why it is
important to have both speakers connected the same way.
Discuss this with your fellow students in the discussion forum!
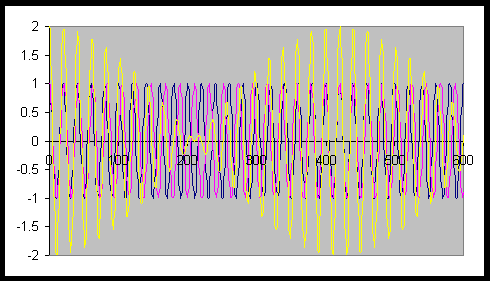 Beats occur when two sounds have nearly,
but not exactly, the same frequency. They are also the result of interference.
Even though a crest may meet a trough at one instant in time at some point in
space (destructive interference), at some later time at the same point a crest
will meet a crest and the amplitudes will add (constructive interference). The
frequency of the beats is equal to the difference in the frequencies of the two
sound waves.
Beats occur when two sounds have nearly,
but not exactly, the same frequency. They are also the result of interference.
Even though a crest may meet a trough at one instant in time at some point in
space (destructive interference), at some later time at the same point a crest
will meet a crest and the amplitudes will add (constructive interference). The
frequency of the beats is equal to the difference in the frequencies of the two
sound waves.
The two waves in the figure on the right have wavelengths of 20 and 21 units
respectively. Their frequencies are v/20 and v/21, where v is the speed of
sound. The frequency of the intensity variations is v/20 - v/21 = v/420.
External link:
The Physics
Classroom: Sound Waves and Music (Lesson 3)
Exploring Interference (a spreadsheet)
Problem:
A "showy" custom-built car has two brass horns that are supposed to produce
the same frequency but actually emit 263.8 and 264.5 Hz. What beat
frequency is produced?
Solution:
- Reasoning:
The frequency of the beats is equal to the difference in the frequencies of
the two sound waves.
- Details of the calculation:
Beat frequency = 264.5 Hz - 263.8 Hz = 0.7 Hz.
Problem:
A piano tuner hears a beat every 2.00 s when listening to a 264.0 Hz tuning
fork and a single piano string. What are the two possible frequencies of
the string?
Solution:
- Reasoning:
The frequency of the beats is equal to the difference in the frequencies of
the two sound waves.
- Details of the calculation:
The beat period is 2s. The beat frequency therefore is ½ s = 0.5s
The two possible frequencies are 264.5Hz and 263.5 Hz.
Embedded Question 2
The label has been scratched off a tuning fork and you need to know its
frequency. From its size, you suspect that it is somewhere around 250 Hz.
You find a 250 Hz tuning fork and a 270 Hz tuning fork. When you strike
the 250 Hz fork and the fork of unknown frequency, a beat frequency of 5 Hz is
produced. When you strike the unknown with the 270 Hz fork, the beat
frequency is 15 Hz. What is the unknown frequency? Could you have
deduced the frequency using just the 250 Hz fork?
Discuss this with your fellow students in the discussion forum!
 Vibrating objects can produce sound. The vibrating object can be a string,
an air column, a membrane, etc. When the object moves outward, it pushes the
air molecules, creating a region of high pressure. When it moves inward it
creates a region of low pressure. As the vibrating object alternately
compresses and expands the surrounding air, the disturbance travels
outward from the source as a longitudinal wave.
Vibrating objects can produce sound. The vibrating object can be a string,
an air column, a membrane, etc. When the object moves outward, it pushes the
air molecules, creating a region of high pressure. When it moves inward it
creates a region of low pressure. As the vibrating object alternately
compresses and expands the surrounding air, the disturbance travels
outward from the source as a longitudinal wave.  The pressure variations ∆P of a sound wave are
usually much smaller than the equilibrium pressure P. For a traveling sound wave in one-dimension we have for
the pressure variations ∆P from equilibrium pressure
The pressure variations ∆P of a sound wave are
usually much smaller than the equilibrium pressure P. For a traveling sound wave in one-dimension we have for
the pressure variations ∆P from equilibrium pressure The displacements of the air molecules from their
equilibrium positions are out of phase with the pressure variation by
π/2. We therefore have for the displacements ∆s
from the equilibrium position
The displacements of the air molecules from their
equilibrium positions are out of phase with the pressure variation by
π/2. We therefore have for the displacements ∆s
from the equilibrium position The speed of sound at standard
temperature and pressure (25 oC, 760 mm of mercury) is 343 m/s (767
miles/h). It is determined by how often the air molecules collide. The speed
of sound increases by about 6 m/s if the temperature increases by 10 oC.
Sound travels faster in liquids and solids than in gases, since the particles in
liquids and solids are closer together and can respond more quickly to the
motion of their neighbors. The speed of sound in water is ~1500 m/s, in iron it
is ~5000 m/s.
The speed of sound at standard
temperature and pressure (25 oC, 760 mm of mercury) is 343 m/s (767
miles/h). It is determined by how often the air molecules collide. The speed
of sound increases by about 6 m/s if the temperature increases by 10 oC.
Sound travels faster in liquids and solids than in gases, since the particles in
liquids and solids are closer together and can respond more quickly to the
motion of their neighbors. The speed of sound in water is ~1500 m/s, in iron it
is ~5000 m/s.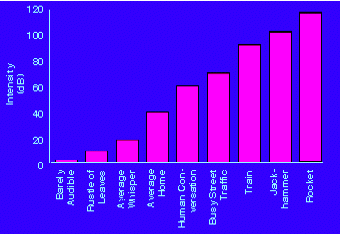
 Like all waves, two or more sound waves traveling through the same medium will
interfere. We can have constructive and destructive interference. If a person
stands equidistant from two speakers which are playing the same sound in phase,
i.e. which are moving in and out together, then the two waves arrive in phase
after traveling the same distance. Crest meets crest and trough meets trough at
the location of the person. The amplitudes of the two waves add and the sound
is loudest here. If the two speakers play the same sound but are out of phase,
i.e. one is moving out while the other is moving in, then the sound has a low
volume at the location of the person equidistant from the two speakers. This
can easily be demonstrated by switching the wires on one of the speakers. (This
is why you need to pay attention to the color of the wires when setting up your
stereo). Dead spots in an auditorium are sometimes produced by destructive
interference.
Like all waves, two or more sound waves traveling through the same medium will
interfere. We can have constructive and destructive interference. If a person
stands equidistant from two speakers which are playing the same sound in phase,
i.e. which are moving in and out together, then the two waves arrive in phase
after traveling the same distance. Crest meets crest and trough meets trough at
the location of the person. The amplitudes of the two waves add and the sound
is loudest here. If the two speakers play the same sound but are out of phase,
i.e. one is moving out while the other is moving in, then the sound has a low
volume at the location of the person equidistant from the two speakers. This
can easily be demonstrated by switching the wires on one of the speakers. (This
is why you need to pay attention to the color of the wires when setting up your
stereo). Dead spots in an auditorium are sometimes produced by destructive
interference. Beats occur when two sounds have nearly,
but not exactly, the same frequency. They are also the result of interference.
Even though a crest may meet a trough at one instant in time at some point in
space (destructive interference), at some later time at the same point a crest
will meet a crest and the amplitudes will add (constructive interference). The
frequency of the beats is equal to the difference in the frequencies of the two
sound waves.
Beats occur when two sounds have nearly,
but not exactly, the same frequency. They are also the result of interference.
Even though a crest may meet a trough at one instant in time at some point in
space (destructive interference), at some later time at the same point a crest
will meet a crest and the amplitudes will add (constructive interference). The
frequency of the beats is equal to the difference in the frequencies of the two
sound waves.