Moving observer

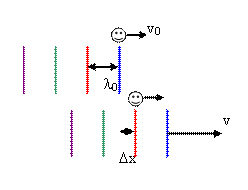Suppose a stationary source is generating sound waves with frequency f₀ = 240 Hz (middle C) and wavelength λ₀ = v/f₀.  A stationary observer a certain distance from the source will hear a sound with pitch f₀.  240 times each second the observer's eardrum will be pushed in and pulled out as pressure crest and pressure trough reach the ear.  The time period between two consecutive crests is T = 1/f₀ = (1/240) s.  Assume the observer gets onto a motorcycle and starts driving away from the source.   Assume that at time t₁ a pressure crest reaches the ear at position x.  The next crest will be at position x at time t₁ + T.  But the ear is no longer there.  The observer has moved.  The crest has to travel an extra distance before it reaches the ear.  This takes an extra time interval ∆t.  The time interval between successive crests reaching the ear of the observer now is T' = T + ∆t.

While the observer has traveled a distance ∆x = v_obs(T + ∆t), the wave has traveled a distance ∆x + λ₀ = v(T + ∆t).
Equating the two expressions for ∆x we obtain
v_obsT + v_obs∆t = vT + v∆t -  λ₀, and, using λ₀ = v/f₀ = vT we have
v_obsT + v_obs∆t = v∆t or ∆t = v_obsT/(v - v_obs).
T' = T + v_obsT/(v - v_obs) = vT/(v - v_obs),
f' = 1/T' = f₀(v - v_obs)/v.
The observer hears a sound with pitch f' < f₀.

The period has increased, the apparent frequency of the wave has decreased, the pitch has decreased.  The observer hears a note lower than middle C.  This is an example of the Doppler effect.

Velocity is a vector.  Let v_obs be the components of the observer's velocity along the direction of the velocity of the sound reaching the observer.  Then v_obs is positive if the observer moves away from the source and v_obs is negative if the observer moves towards the source.  With this sign convention f' = f₀(v - v_obs)/v also gives the frequency f' heard by an observer moving towards the source.

If the observer is driving towards the source, then the time interval between successive crests reaching the ear will be shorter than T.  Assume that at time t₁ a pressure crest reaches the ear at position x.  The next crest will be at position x at time t₁ + T.  But it will reach the ear before it reaches position x, because the observer is moving towards the source.  The observer hears a note higher than middle C.
The apparent frequency of the sound wave reaching the observer is
f' = f₀(v - v_obs)/v= f = f₀(v + |v_obs|)/v.
f' > f₀,  the observer hears a higher frequency sound.

We usually do not notice the Doppler effect when moving around on foot, because the speed of sound is so much greater than our speed.  But moving on a motorcycle at 55 miles/h = 24.6 m/s towards a source, we have f = f₀(340 + 24.6)/340 = 1.07 f₀.  Moving away from the source we have f = f₀(340 - 24.6)/340 = 0.93 f₀.  As we drive by the source, the perceived pitch therefore changes by approximately 14%, a noticeable change.

Moving Sources

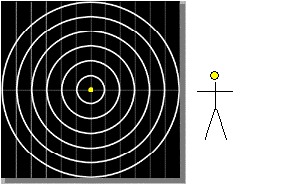The perceived pitch of a sound wave also changes if the observer is stationary and the source is moving.  Let v_s be the components of the source's velocity along the direction of the velocity of the sound reaching the observer.  Then v_s is positive if the source moves towards the observer and  v_s is negative if the source moves away from the observer.  The apparent frequency of the sound wave reaching the observer is
f' = f₀v/(v - v_s).

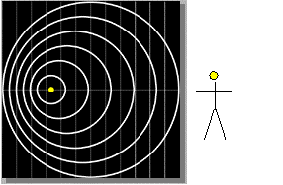
In the figure on the right the rings denote successive crests of the sound wave.  The time interval between the emission of successive crests is T.  The larger the ring, the earlier is the time of emission.  All the rings expand with the same speed, the speed of sound in the medium.  If the observer is stationary, then the time interval between the arrival of successive rings at the ear is T.

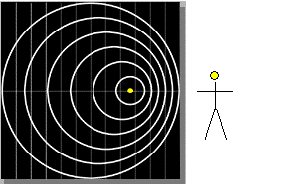In the next figure the source is moving towards the observer.  The center of each ring is at the position of the source at the time it emits the crest.  Since the source is moving towards the right, the center of successive rings moves towards the right.  If the observer is stationary, then the time interval between the arrival of successive rings at the ear is less than T.

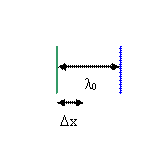In the time interval T the wave travels a distance λ₀ and the source travels a distance ∆x.
λ₀/v = ∆x/v_s.
The wavelength at the observer is λ' = λ₀ - ∆x = λ₀ - λ₀v_s/v = λ₀ (v - v_s)/v.
f' = v/λ' = (v/λ₀)[v/(v - v_s)] = f₀v/(v - v_s).

In the next figure the source is moving away from the observer.  Since the source is moving towards the left, the center of successive rings moves towards the left.  If the observer is stationary, then the time interval between the arrivals of successive rings at the ear is greater than T.

The apparent frequency of the sound wave reaching the observer is
f' = f₀v/(v - v_s) = f₀v/(v + |v_s|).

Please click here to for an interactive visualization of sound waves close to a cylindrical speaker.
Compare sound wave with different wavelengths, produced when the speaker is at rest and when it is moving.

Whenever the source and the observer move with respect to each other, the wavelength of the sound reaching the ear will be Doppler shifted.  But the formula for the Doppler shift depends on who is moving, the source or the observer.  If the source is moving towards the observer with a speed close to the speed of sound, then the wavelength of the sound reaching the ear becomes very short and the pitch becomes very high.  In the formula, f' = f₀v/(v - v_s), the denominator gets very small.  When v_s = v , the denominator is zero, so f' becomes infinite.  A sonic boom is produced at the location of the observer.

If both source and observer are in motion, then the apparent frequency of the sound wave reaching the observer is

f' = f₀(v - v_obs)/(v - v_s)

where v_obs and v_s are not the speeds, but the components of the observer's and the source's velocity in the direction of the velocity of the sound reaching the observer. 
f' increases if the source and the observer approach each other and decreases if they recede from each other.

External link:  The Doppler shift and sonic boom

Problem:

A train has a whistle, which emits a 400 Hz sound.  You are stationary and you hear the whistle, but the pitch is 440 Hz.  How fast is train moving towards or away from you?

Solution:

• Reasoning:
  The pitch is higher, so the train is moving towards you. 
  Its speed relative to you is found from f = f₀v/(v-v_s).
• Details of the calculation:
  We have (v-v_s) = f₀v/f = (400/s)(340 m/s)/(440/s) = 309 m/s. 
  Therefore v_s = 340 m/s-309 m/s = 31 m/s = 69 mph.
  v_s is positive, the train is moving in the direction of the sound, towards you.

Problem:

Two eagles fly directly toward one another, the first at 15.0 m/s and the second at 20.0 m/s.  Both screech, the first one emitting a frequency of 3200 Hz and the second one emitting a frequency of 3800 Hz.  What frequencies do they receive if the speed of sound is 330 m/s?

Solution:

• Reasoning:
  Both source and observer are in motion, so f = f₀(v - v_obs)/(v - v_s).
• Details of the calculation:
  (i)  The first eagle is the source, the second the observer.  Then v_s = 15 m/s, v_obs = -20 m/s, f₀ = 3200/s.
  The second eagle hears a screech with frequency f = 3200/s*(330 + 20)/(330 - 15) = 3556/s.
  (i)  The second eagle is the source, the first the observer.  Then v_s = 20 m/s, v_obs = -15 m/s, f₀ = 3800/s.
  The first eagle hears a screech with frequency f = 3800/s*(330 + 15)/(330 - 20) = 4229 s.

The Doppler effect is a phenomenon observed with all waves.  It is named for the Austrian scientist Christian Doppler (1803-1853).  Whenever a source generating a wave moves relative to an observer or an observer moves relative to a source, the frequency of the wave at the location of the observer is shifted relative to the frequency of the source.  The frequency at the location of the observer increases when the source and observer are approaching each other and decreases when they are moving away from each other.