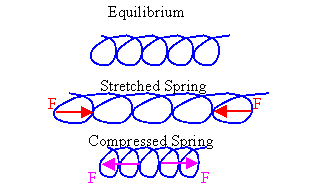
 A ideal spring has
an equilibrium length. If a spring is compressed, then a force
with magnitude proportional to the decrease in length from the
equilibrium length is pushing each end away from the other. If a
spring is stretched, then a force with magnitude proportional to the
increase in length from the equilibrium length is pulling each end
towards the other.
A ideal spring has
an equilibrium length. If a spring is compressed, then a force
with magnitude proportional to the decrease in length from the
equilibrium length is pushing each end away from the other. If a
spring is stretched, then a force with magnitude proportional to the
increase in length from the equilibrium length is pulling each end
towards the other.
 The force exerted by a spring on
objects attached to its ends is proportional to the spring's change
in length away from its equilibrium length and is always directed
towards its equilibrium position.
The force exerted by a spring on
objects attached to its ends is proportional to the spring's change
in length away from its equilibrium length and is always directed
towards its equilibrium position.
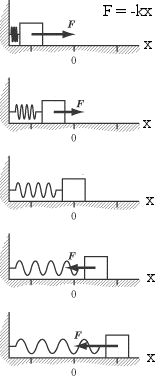
Assume one end of a spring is fixed to a wall or ceiling and an
object pulls or pushes on the other end. The object exerts a force
on the spring and the spring exerts a force on the object. The
force F the spring exerts on the object is in a direction opposite to the
displacement of the free end. If the x-axis of a coordinate system is
chosen parallel to the spring and the equilibrium position of the free end of
the spring is at x = 0, then
F = -kx.
The proportional constant k is called the
spring constant. It is a
measure of the spring's stiffness.
When an ideal spring is stretched or compressed, so that
its length changes by an amount x from its equilibrium
length, then it exerts a force F = -kx in a direction
towards its equilibrium position. The force a spring exerts is a restoring force, it acts to
restore the spring to its equilibrium length.
 Problem:
Problem:
A stretched spring supports a 0.1 N weight. Adding another 0.1 N
weight, stretches the string by an additional 3.5 cm. What is the
spring constant k of the spring?
Solution:
- Reasoning:
An ideal spring obeys Hooke's law, F = -kx. The initial stretch is not
given. Let us call it x0.
0.1 N = -kx0. 0.2 N = -k(x0 + 0.035 m).
Subtracting the first from the second equation we have
0.1 N = -k*0.035 m.
- Details of the calculation:
k = |F/x| = (0.1 N)/ (0.035 m) = 2.85 N/m.
 You want to know your weight. You get onto the bathroom scale. You want to
know how much cabbage you are buying in the grocery store. You put the cabbage
onto the scale in the grocery store.
You want to know your weight. You get onto the bathroom scale. You want to
know how much cabbage you are buying in the grocery store. You put the cabbage
onto the scale in the grocery store.
The bathroom scale and the scale in the grocery
store are probably spring scales. They operate on a simple
principle. They measure the stretch or the compression of a
spring. When you stand still on the bathroom scale the total force
on you is zero. Gravity acts on you in the downward direction, and
the spring in the scale pushes on you in the upward direction. The
two forces have the same magnitude.
Since the force the spring exerts on you is equal in magnitude to
your weight, you exert a force equal to your weight on the spring,
compressing it. The change in length of the spring is proportional
to your weight.
Spring scales use a spring of known spring constant and provide a calibrated readout of the amount of stretch or
compression. Spring scales measure forces. They determine the weight of an
object. On the surface of the earth weight and mass are proportional to each
other, w = mg, so the readout can easily be calibrated in units of force (N or
lb) or in units of mass (kg). On the moon, your bathroom spring scale
calibrated in units of force would accurately report that your weight has
decreased, but your spring scale calibrated in units of mass would inaccurately
report that your mass has decreased.
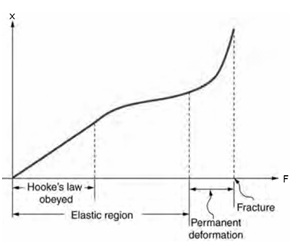 Spring scales obey Hooke's law, F
= -kx. Hooke's law is remarkably general. Almost any object that can be
distorted pushes or pulls with a restoring force proportional to the
displacement from equilibrium towards the equilibrium position, for very small
displacements. However, when the displacements become large, the
elastic limit is reached. The stiffer the
object, the smaller the displacement it can tolerate before the elastic limit is
reached. If you distort an object beyond the elastic limit, you are likely to
cause permanent distortion or to break the object.
Spring scales obey Hooke's law, F
= -kx. Hooke's law is remarkably general. Almost any object that can be
distorted pushes or pulls with a restoring force proportional to the
displacement from equilibrium towards the equilibrium position, for very small
displacements. However, when the displacements become large, the
elastic limit is reached. The stiffer the
object, the smaller the displacement it can tolerate before the elastic limit is
reached. If you distort an object beyond the elastic limit, you are likely to
cause permanent distortion or to break the object.
The elastic properties of linear objects, such as wires, rods, and columns
which can be stretched or compressed, can be described by a parameter called the
Young's modulus of the material.
Before the elastic limit is reached, Young's modulus Y is the ratio of the force
per unit area F/A, called the stress, to the fractional change in length ∆L/L.
(This is an equation relating magnitudes. All quantities are positive.)
Y = (F/A)/(∆L/L), F/A = Y∆L/L.
Young's modulus is a property of the material. It
can be used to predict
the elongation or compression of an object before the elastic limit is reached.
Problem:
Consider a metal bar of initial length L and cross-sectional area A.
The Young's modulus of the material of the bar is Y. Find the "spring
constant" k of such a bar for low values of tensile strain.
Solution:
- Reasoning:
From the definition of Young's modulus: F = Y A ∆L/L.
From the definition of the spring constant: F = k∆L. (Equation,
relating magnitudes, ∆L = magnitude of the displacement from
equilibrium.)
Therefore k = Y A/L.
Problem:
Consider a steel guitar string of initial length L = 1 m and cross-sectional
area A = 0.5 mm2.
The Young's modulus of the steel is Y = 2*1011
N/m2.
How much would such a string stretch under a tension of
1500 N?
Solution:
- Reasoning:
From the definition of Young's modulus Y = (F/A)/(∆L/L), we have ∆L =
F*L/(Y*A).
- Details of the calculation:
∆L = F*L/(Y*A) = 1500 N*(1 m)/(2*1011 N/m2*0.5 mm2*(1
m/103 mm)2) = 0.015 m = 15 mm.
Consider a point object, i.e. for the moment let us neglect any possible
rotation of the object. If this object is at rest and the net force acting
on the object is zero, the object is at an equilibrium position. If, when
slightly disturbed, the object is acted on by a restoring force pointing to
its equilibrium position, it is said to be in stable
equilibrium. Objects suspended on springs are in
stable equilibrium. An object sitting on top of a ball, on the other hand, is
in unstable equilibrium. When disturbed, it
is acted on by a force pointing away from the equilibrium position.
Example:
A ball and a bowl
(a) The ball is in stable equilibrium at the bottom of a bowl.
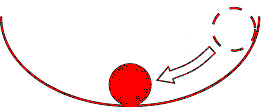
(b) The ball is in unstable equilibrium at the top of a bowl.

 A ideal spring has
an equilibrium length. If a spring is compressed, then a force
with magnitude proportional to the decrease in length from the
equilibrium length is pushing each end away from the other. If a
spring is stretched, then a force with magnitude proportional to the
increase in length from the equilibrium length is pulling each end
towards the other.
A ideal spring has
an equilibrium length. If a spring is compressed, then a force
with magnitude proportional to the decrease in length from the
equilibrium length is pushing each end away from the other. If a
spring is stretched, then a force with magnitude proportional to the
increase in length from the equilibrium length is pulling each end
towards the other. The force exerted by a spring on
objects attached to its ends is proportional to the spring's change
in length away from its equilibrium length and is always directed
towards its equilibrium position.
The force exerted by a spring on
objects attached to its ends is proportional to the spring's change
in length away from its equilibrium length and is always directed
towards its equilibrium position. Problem:
Problem: You want to know your weight. You get onto the bathroom scale. You want to
know how much cabbage you are buying in the grocery store. You put the cabbage
onto the scale in the grocery store.
You want to know your weight. You get onto the bathroom scale. You want to
know how much cabbage you are buying in the grocery store. You put the cabbage
onto the scale in the grocery store. Spring scales obey Hooke's law, F
= -kx. Hooke's law is remarkably general. Almost any object that can be
distorted pushes or pulls with a restoring force proportional to the
displacement from equilibrium towards the equilibrium position, for very small
displacements. However, when the displacements become large, the
elastic limit is reached. The stiffer the
object, the smaller the displacement it can tolerate before the elastic limit is
reached. If you distort an object beyond the elastic limit, you are likely to
cause permanent distortion or to break the object.
Spring scales obey Hooke's law, F
= -kx. Hooke's law is remarkably general. Almost any object that can be
distorted pushes or pulls with a restoring force proportional to the
displacement from equilibrium towards the equilibrium position, for very small
displacements. However, when the displacements become large, the
elastic limit is reached. The stiffer the
object, the smaller the displacement it can tolerate before the elastic limit is
reached. If you distort an object beyond the elastic limit, you are likely to
cause permanent distortion or to break the object.
