Fictitious Forces
Newton's first law, also called the law of inertia,
defines a special class of reference frames, called inertial frames.
It states that, when viewed in an inertial reference frame, an object at rest
remains at rest and an object in motion continues in motion with constant
velocity unless it is acted on by an external net force. Newton's second law
and Newton's third law correctly describe the motion of objects as viewed
by observers in inertial reference frames. In an inertial frame
F = ma, where the net force
F is the vector sum of all the
real known forces acting on an object of mass m.
If observers at rest in an accelerating frame want to use F = ma
to predict the motion of an objet in their reference frame, then
F has to
include not only the vector sum of all the real known forces acting on the
object but also a fictitious force. Fictitious forces appear in
accelerating frames.
 You just got your new car. You want to experience it. You want to "feel"
its power. You floor the gas pedal, and you experience a force pressing you
back into your seat. Where does this force come from?
You just got your new car. You want to experience it. You want to "feel"
its power. You floor the gas pedal, and you experience a force pressing you
back into your seat. Where does this force come from?
This force is a fictitious force. Fictitious forces
appear in accelerating reference frames. Such frames are
NOT inertial reference frames. The accelerating
reference frame in the above example is accelerating with your car. In this
frame your car and you are at rest. But you are feeling a force pushing you
against the back of your seat. To your friend observing you from the sidewalk
things look different. The motor is responsible for the forward acceleration of
the car. Because of your mass, you have inertia. Without a force acting on
you, you would remain at rest with respect to the sidewalk. To keep you
accelerating forward, the back of the seat has to push on you. (You will be
pushing on the seat with a force equal in magnitude, but opposite in
direction.) The fictitious force appearing in the accelerating frame is the
negative of the the real force responsible for maintaining your acceleration and
keeping you at rest in the accelerating frame. The real force acting on you is
in the forward direction, while the fictitious force experienced in the
accelerating frame is in the backward direction.
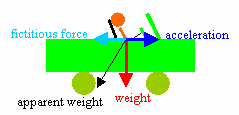
In the accelerating frame of the car, you experience
the fictitious force in the backward direction and your weight, pointing
down. The net force experienced is the vector sum of these two forces.
This force becomes your apparent weight,
which points in a direction backward and down.
The apparent weight of
an accelerating object is the vector sum of its real weight and
the negative of all the forces that produce the object's acceleration
a = dv/dt.
wapparent = wreal - ma.
 When you stand on a bathroom scale in an inertial frame, such as in your
bathroom, the scale reading is proportional to your real weight. When you
stand on a bathroom scale in an accelerating frame, such as an elevator
accelerating upward, its reading is proportional to your apparent weight.
When you stand on a bathroom scale in an inertial frame, such as in your
bathroom, the scale reading is proportional to your real weight. When you
stand on a bathroom scale in an accelerating frame, such as an elevator
accelerating upward, its reading is proportional to your apparent weight.
For the elevator accelerating upward:
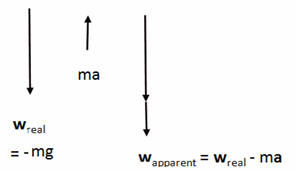
In every accelerating frame we have wapparent =
wreal - ma. The apparent weight of a mass m is
its real weight minus its mass times the acceleration of the frame (vector
addition).
Assume you are riding on a merry-go-round. A reference frame in which you
are stationary, i.e. a frame that is moving with you as you are moving along a
circular path, is also an accelerating frame. This frame is moving with
constant speed, but the direction of its velocity is constantly changing. You
are sitting still on your seat while the merry-go-round is turning. But
something seems to be pulling you towards the outside, away from the center.
You experience a fictitious force. To your friend on the ground things again
look different. You are moving in a circle. The direction of your velocity is
constantly changing. You are accelerating. The direction of your acceleration
is towards the center of the circle, so there must be a force pushing or pulling
you toward the center. If you are sitting in a seat, the wall of the seat will
be pushing against you, pushing you towards the center.
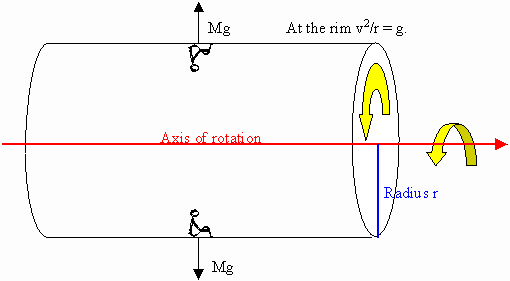
In many Science Fiction books, humans live in space in a space station that
is rotating about a central axis. Their real weight is close to zero. The
acceleration of a person with mass M at rest with respect to the space station
near the rim is a = v2/r directed towards the axis. The
apparent weight of the person is wapparent = wreal
- Ma = Mv2/r directed towards the rim.
If the rim is the floor of some room without windows, and the rotation speed and
the radius of the station are adjusted so that a = v2/r = g, then
there is no way a human or a scientific instrument in the room can distinguish
between the apparent weight and the force of gravity. If the human steps on a
scale, the scale will read the same "weight" as it does on the surface on
earth. If the human throws a ball near the "surface", the ball will follow the
same trajectory it would on earth.
Problem:
Engineers are trying to create artificial gravity in a ring-shaped space
station by spinning it like a centrifuge. The ring is 100 m in radius. How
quickly must the space station turn in order to give the astronauts inside it
apparent weights equal to their real weights at the earth's surface
Solution:
- Reasoning:
We want a = v2/r = g , or v2 = gr.
- Details of the calculation:
v2 = gr = (9.8 m/s2)(100
m) = 980 (m/s)2. Therefore v = 31.3 m/s.
The circumference of the space station is 2πr = 628 m.
The space station therefore completes a turn in (628 m)/(31.3 m/s) = 20 s.
Embedded Question 2
Is there a real force that throws water from clothes during the spin cycle of
a washing machine? Explain how the water is removed.
Discuss this with your fellow students in the discussion forum!
 You just got your new car. You want to experience it. You want to "feel"
its power. You floor the gas pedal, and you experience a force pressing you
back into your seat. Where does this force come from?
You just got your new car. You want to experience it. You want to "feel"
its power. You floor the gas pedal, and you experience a force pressing you
back into your seat. Where does this force come from? When you stand on a bathroom scale in an inertial frame, such as in your
bathroom, the scale reading is proportional to your real weight. When you
stand on a bathroom scale in an accelerating frame, such as an elevator
accelerating upward, its reading is proportional to your apparent weight.
When you stand on a bathroom scale in an inertial frame, such as in your
bathroom, the scale reading is proportional to your real weight. When you
stand on a bathroom scale in an accelerating frame, such as an elevator
accelerating upward, its reading is proportional to your apparent weight.

