The gravitational potential energy U_g is defined as the negative of the work done by the gravitational force, or the work done by an applied force canceling the gravitational force, in displacing an object from a reference position.  If the gravitational force acting on an object is pointing in the -y direction with constant magnitude mg, and the reference position is at y = 0, then U_g = mgy.

The zero of the gravitational potential energy, i.e. the reference position, is chosen arbitrarily.  However a difference in gravitational potential energy

∆U_g = mg∆y = mg(y_f - y_i)

is uniquely defined.

The gravitational potential energy gained by an object being lifted is equal to the work done on the object by an applied force, which exactly cancels gravity.  The applied force does positive work.  When the object is being lifted, the gravitational force does negative work.  The gravitational potential energy can be converted back into other forms by letting the gravitational force do positive work.  If we let the object fall towards the ground it will lose potential energy and gain kinetic energy.

Problem:

A 100 N crate sits on the ground and is attached to one end of a rope.  A person on a balcony pulls up on the rope, lifting the crate a distance of 3 m.  What is the change in the gravitational potential energy of the crate?

Solution:

• Reasoning:
  Near the surface of Earth the change in the gravitational potential energy id ∆U_g = mg∆y, with the y-axis pointing up.
• Details of the calculation:
  ∆U_g = mg∆y = 100 N* 3m = 300 J.  (Note:  100 N is the weight of the crate, i.e. the gravitational force mg acting on it.  The mass of the crate is m = 100 N/9.8 m/s² = 10.1 kg.)

Problem:

A 100 N crate sits on the ground and is attached to one end of a rope.  A person on a balcony pulls up on the rope with a constant force of 110 N lifting the crate a distance of 3 m.
What is the kinetic energy of the crate when it reaches the height of 3 m?

Solution:

• Reasoning:
  The net force on the crate is the difference between upward force from the rope and the downward force of gravity.
  F_net*d = W_net = ∆K.  (work - kinetic energy theorem)
• Details of the calculation:
  F_net = 110 N - 100 N = 10 N.   W_net = 10N * 3 m = 30 J = ∆K.
  Since the crate starts with zero kinetic energy, its final kinetic energy is 30 J.
  The applied force does 110 N * 3 m = 330 J of work.  300 N is converted into potential energy and 30 N into kinetic energy.

Conservative Forces

The gravitational potential energy does not depend on the path.

Example:

We do the same work lifting the motorcycle straight up onto the bed of the truck or rolling it up a ramp.

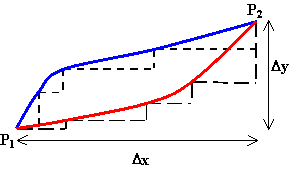
The gravitational force near the surface of the earth points vertically downward.  We can approximate any path between two points P₁ and P₂ by arbitrarily small vertical and horizontal segments.  The total horizontal and the total vertical displacement are the same for each path.  The gravitational force does no work along the horizontal segments of the path, since here it is perpendicular to displacement vector.  It does work W_i = -mg∆y_i along each vertical segment of length ∆y_i.  The total work done by the gravitational force is W = -mg∆y_total = -mgh.  The change in potential energy is U_g = mgh.

A potential energy function is a function of the position of an object.  It can be defined only for conservative forces.  A force is conservative if the work it does on an object depends only on the initial and final position of the object and not on the path.  The gravitational force is a conservative force.  The potential energy function associated with the gravitational force near the surface of the earth is U_g = mgy if the reference point is chosen at y = 0.  (U_g only depends on the position of an object, not on how the object reached that position.)

Another example of a conservative force is the force exerted by a spring.  The elastic potential energy function is U_s = ½kx², where x is the displacement from equilibrium.  U_s only depends on how much the spring is stretched or compressed, not on how this was accomplished.

Problem:

A 100 N force is used to stretch a spring with spring constant k = 2000 N/m.
(a)  What is the maximum stretch this force can produce?
(b)  How much elastic potential energy is stored in the spring at the maximum stretch?

Solution:

• Reasoning:
  The spring obeys Hooke's law.  At maximum stretch F_ext = kx.
  The elastic potential energy stored in the spring is U_s = ½kx².
• Details of the calculation:
  (a)   x = F_ext/k = (100 N)/(2000 N/m) = 0.05 m = 5 cm.
  (b)  The elastic potential energy stored in the spring is
  U_s = ½kx² = ½(2000 N/m)(0.05 m)² = 2.5 J.

When the a conservative force does work on an object, the potential energy of the object changes.  We may write

F_x∆x = -∆U or F_x = -∆U/∆x.

F_x = -∆U/∆x (as ∆x --> 0) holds for any conservative force in one dimension.  If we know the potential energy function for the object, we can calculate the conservative force acting on the object.

The conservative internal force acting between parts of the system equals the negative derivative of the potential energy associated with that system.

Embedded Question 1

Does the work you do on a book when you lift it onto a shelf depend on the path taken?  On the time taken?  On the height of the shelf?  On the mass of the book?

Discuss this with your fellow students in the discussion forum!