The vector product of two vectors A and B is defined as the vector C = A × B.

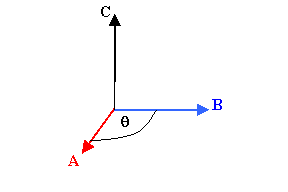
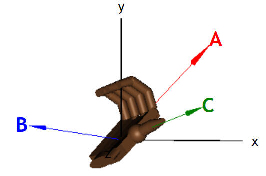
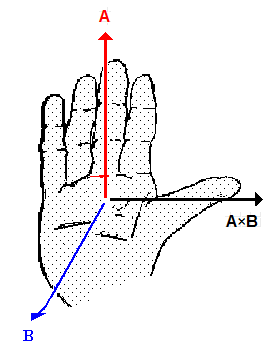
The magnitude of C is C = A B sinθ, where θ is the smallest angle between the directions of the vectors A and B.  C is perpendicular to both A and B, i.e.  it is perpendicular to the plane that contains both A and B.  The direction of C can be found by using the right-hand rule.
Let the fingers of your right hand point in the direction of A.  Orient the palm of your hand so that, as you curl your fingers, you can sweep them over to point in the direction of B.  Your thumb points in the direction of C = A × B.

If A and B are parallel or anti-parallel to each other, then C = A × B = 0, since sinθ = 0.  If A and B are perpendicular to each other, then sinθ = 1 and C has its maximum possible magnitude.

Please click on the image below for an animation!

We can find the Cartesian components of C = A × B in terms of the components of A and B.

C_x = A_yB_z - A_zB_y
C_y = A_zB_x - A_xB_z
C_z = A_xB_y - A_yB_x