Near the surface of Earth, object with weight can float in fluids.  The fluid must exert a force on a floating object equal in magnitude and opposite in direction to the object's weight.  Where does this force come from?

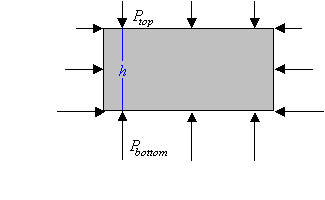Consider again the box-shaped volume of water in equilibrium at some depth in the pool.  The upward force provided by the surrounding water must exactly balance the force of gravity acting on the water in the box.  The upward force provided by the surrounding water must be equal to the weight of water in the box.

If we replace the volume of water with a box of the same shape containing some other material, then the net upward force provided by the surrounding water does not change.  It depends only on the difference in the pressure at the top and at the bottom of the box.  But the weight of the box changes, and therefore the net force on the box changes.  If the weight is greater than that of the corresponding volume of water, the net force is downward and the box will accelerate downward and fall.  If the weight is less than that of the corresponding volume of water, the net force is upward and the box will accelerate upward and rise. 

This is Archimedes' principle.  It holds for all fluids, i.e. it holds for all liquids and gases. 
An object partially or wholly immersed in a gas or liquid is acted upon by an upward buoyant force B equal to the weight w of the gas or liquid it displaces.

B = w

Problem:

A 2 kg block of wood is floating in water.  What is the magnitude of the buoyant force acting on the block?

Solution:

• Reasoning:
  The block is floating, it is not accelerating, the net force must be zero.  So the magnitude of the buoyant force must be equal the weight. 
• Details of the calculation:
  B = mg = 19.6 N.

Problem:

The density of freshwater is 1 g/cm³ and the density of seawater is 1.03 g/cm³.  Will a ship float higher in freshwater or seawater?

Solution:

• Reasoning:
  When an object floats, the weight of the displaced water equals the weight of the object.  You need less of the denser seawater to make up the weight of the ship than you need of the less dense fresh water.  Therefore the ship displaces less seawater and floats higher in seawater.

Problem:

A Styrofoam slab has a thickness h and a density ρ_object.  What is the area of the slab, if it floats with its top surface just awash in fresh water when a swimmer of mass m is on top?

Solution:

• Reasoning:
  When an object floats, the magnitude of the buoyant force is equal to the magnitude of its weight.  The magnitude of the buoyant force is equal to the magnitude of the weight w_water of the displaced water.
• Details of the calculation:
  w_water = ρ_waterAhg, where A is the area of the slab. 
  The the magnitude of the weight of the object is  w_object = ρ_objectAhg + mg. 
  We need w_water = w_object.
  ρ_waterAhg = ρ_objectAhg + mg.
  ρ_waterAh - ρ_objectAh = m.
  A = m/(ρ_waterh - ρ_objecth).

Problem:

A frog in a hemispherical pod finds that he just floats without sinking into a sea of blue-green ooze with density 1.35 g/cm³.  If the pod has radius 6 cm and negligible mass, what is the mass of the frog?

Solution:

• Reasoning:
  When an object floats, the magnitude of the buoyant force is equal to the magnitude of its weight.  The magnitude of the buoyant force is equal to the magnitude of the weight w_liquid of the displaced liquid.
• Details of the calculation:
  w_liquid = ρ_liquidVg. 
  The volume V of the displaced liquid is the volume of one half sphere,
  V = 2πr³/3 = 2π(6 cm)³/3 = 452 cm³. 
  The magnitude of the weight of the object is w_object = m_frogg.  (We are neglecting the weight of the air-filled pod.)
  ρ_liquidVg = m_frogg. 
  m_frog = 1.35 (g/cm³) 452 cm³ = 610 g. 

Problem:

A barge is carrying a load of gravel along a river.  It approaches a low bridge, and the captain realizes that the top of the pile of gravel is not going to make it under the bridge.  The captain orders the crew to quickly shovel gravel from the pile into the water.  Is this a good decision?

Solution:

• Reasoning:
  Assume an object has a weight w and a density ρ greater than that of water.  When the object floats in a boat, the weight of the water displaced because of this object is equal to the weight of the object.  When the object sinks when thrown overboard, the weight of the displaced water is less than the weight of the object.  An object with ρ > ρ_water of a given weight displaces more water when floating than when being submerged.  When a given volume of gravel is shoveled into the water, a larger volume of the ship will rise out of the water.  But that does not necessarily mean that the maximum height h of the load above the water's surface increases.  This maximum height h depends on how the load is distributed.  If the load is evenly spread over the entire deck of the ship, the shoveling sand into the water is not a good idea.  But if the load is a pyramid-shaped pile, then removing the top of the pyramid is a good idea.

Problem:

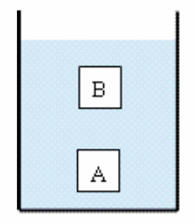Two objects, A and B, have the same volume and are completely submerged in a liquid, although A is deeper than B. Which object, if either, experiences the greater buoyant force?

Solution:

• Reasoning:
  The buoyant force B equal is equal in magnitude to the weight w of the displaced liquid. Both objects displace the same amount of liquid and therefore experience the same buoyant force.
  (Even though the average pressure is higher at the position of A than at the position of B, the difference between pressures on the top and on the bottom of each block is the same.  It is this pressure difference that is responsible for the buoyancy.)
  Watch this short video clip!

External link:  Buoyancy

AI Study Tip:

Example prompts: 

Why does an object feel lighter when submerged in water?  Explain the relationship between the weight of the displaced fluid and the buoyant force using Archimedes' Principle.

I have a problem where a block of wood with a density of 600 kg/m³ is floating in water.  Can you show me the algebraic steps to find what percentage of the block is submerged?

Embedded Question 2

Do fluids exert buoyant forces in a "weightless" environment, such as in the space shuttle?  Explain your answer.

Discuss this with your fellow students in the discussion forum!