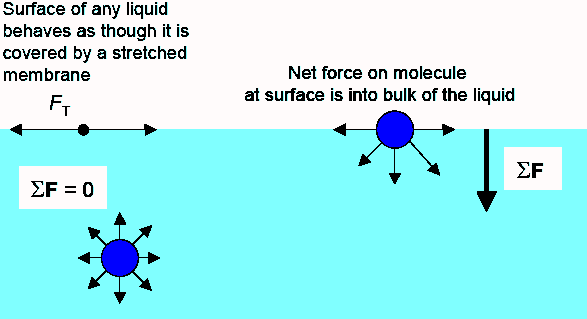
 The surface of a liquid behaves as though it is covered by a
stretched membrane. The strength of the membrane depends on the liquid.
It is, for example, much higher for pure water than for soapy water.
Cohesive forces that act between the molecules of the liquid without
chemical bonding give rise to the surface tension. [Molecules
in liquids experience strong intermolecular attractive forces. When those forces
act between like molecules, they are referred to as cohesive forces. When the
attractive forces act between unlike molecules, they are said to be adhesive
forces.]
The surface of a liquid behaves as though it is covered by a
stretched membrane. The strength of the membrane depends on the liquid.
It is, for example, much higher for pure water than for soapy water.
Cohesive forces that act between the molecules of the liquid without
chemical bonding give rise to the surface tension. [Molecules
in liquids experience strong intermolecular attractive forces. When those forces
act between like molecules, they are referred to as cohesive forces. When the
attractive forces act between unlike molecules, they are said to be adhesive
forces.]
The molecules at the surface do not have other neighbors of the same kind on
all sides. They experience a net attractive force toward the bulk of the
liquid. This force results in a surface "film" which makes it more
difficult to move an object through the surface than to move it, when it is
completely submersed.
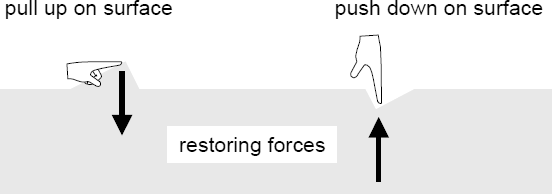 The surface of a liquid behaves like an elastic membrane. A surface
molecule which is displaced by a small amount is acted on by a restoring force
due to cohesive forces.
The surface of a liquid behaves like an elastic membrane. A surface
molecule which is displaced by a small amount is acted on by a restoring force
due to cohesive forces.
If there are no competing external forces present, a liquid system will
minimize its surface area. Soap bubbles and raindrops are spherical
because the sphere is the shape with the smallest surface to volume ratio.
The surface tension γ is defined as the force along a line of unit length.
The force is parallel to the surface and perpendicular to the line.
Surface tension is therefore measured in units of N/m in SI units. The
surface tension γ for different surfaces is listed in the table below.
| Liquid |
Surface Tension γ (N/m) |
| water (20 oC) |
0.073 |
| water (100 oC) |
0.059 |
| soapy water (20 oC) |
0.025 |
| alcohol |
0.022 |
| glycerine |
0.063 |
| mercury |
0.513 |
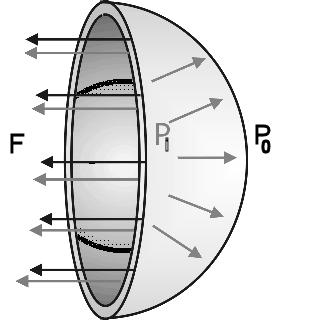 Picture a soap bubble. The surface tension balances the outward force
due to the pressure difference between the inside and the outside air. We have two surfaces, the inner and the outer
surface of the bubble. The force from surface tension is F = 2γL =
2γ2πr = 4γπr. For the bubble to be stable and not
collapse, the pressure inside the bubble must be higher than the
pressure on the outside. The force due to the pressure difference
must balance the force from the surface tension. The force to the
pressure difference is (Pi - Po)πr2.
Picture a soap bubble. The surface tension balances the outward force
due to the pressure difference between the inside and the outside air. We have two surfaces, the inner and the outer
surface of the bubble. The force from surface tension is F = 2γL =
2γ2πr = 4γπr. For the bubble to be stable and not
collapse, the pressure inside the bubble must be higher than the
pressure on the outside. The force due to the pressure difference
must balance the force from the surface tension. The force to the
pressure difference is (Pi - Po)πr2.
For a single spherical surface balance is achieved if
Pi - Po = 2γ/r. This is
known as Laplace's law for a spherical membrane.
For a
soap bubble with two surfaces Pi - Po = 4γ/r.
Problem:
Calculate the gauge pressure inside a soap bubble 2 cm in radius using the surface tension
for soapy water γ = 0.025 N/m.
Solution:
- Reasoning:
Use Laplace's law for a spherical membrane. For a
soap bubble with two surfaces Pi - Po = 4γ/r.
- Details of the calculation:
Pi - Po = 4γ/r. Po =
atmospheric pressure, so Pi - Po = gauge
pressure.
Pi - Po = (4*0.025 N/m)/(0.02 m) = 5 Pa.
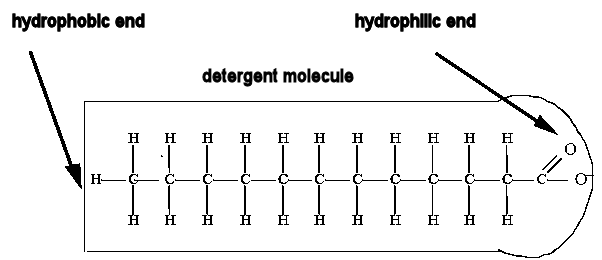 Detergents lower the surface tension of water. Detergent
molecules have two ends, one hydrophobic end, repelled by water and one hydrophilic end, attracted to water.
Detergents lower the surface tension of water. Detergent
molecules have two ends, one hydrophobic end, repelled by water and one hydrophilic end, attracted to water.
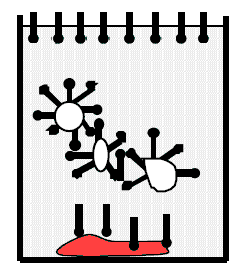 In water detergent molecules on the surface are aligned with
their hydrophobic ends away from the surface. They break the surface and
thus lower the surface tension. Other detergent molecules are dispersed
throughout the water. Particles of organic matter are rendered soluble by
being coated with these detergent molecules. The hydrophobic ends stick to
the particles and the hydrophilic ends point outwards.
In water detergent molecules on the surface are aligned with
their hydrophobic ends away from the surface. They break the surface and
thus lower the surface tension. Other detergent molecules are dispersed
throughout the water. Particles of organic matter are rendered soluble by
being coated with these detergent molecules. The hydrophobic ends stick to
the particles and the hydrophilic ends point outwards.
 Wetting is the ability of liquids to form interfaces with solid surfaces. The
contact angle θ
between the liquid and the solid surface is a measure of the degree of
wetting. A smaller the contact angle and a smaller the surface
tension result in a greater the degree of wetting.
Wetting is the ability of liquids to form interfaces with solid surfaces. The
contact angle θ
between the liquid and the solid surface is a measure of the degree of
wetting. A smaller the contact angle and a smaller the surface
tension result in a greater the degree of wetting.
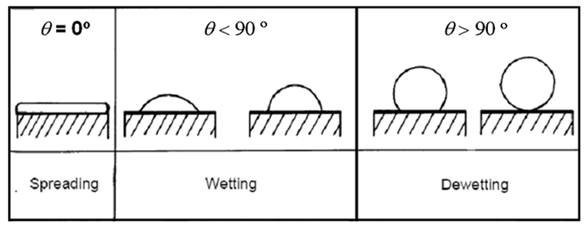 When adhesive forces are greater than cohesive forces, the
contact angle θ lies between 0 and 90o. When adhesive
forces are smaller than cohesive forces, the contact angle θ lies between 90o and 180o.
When adhesive forces are greater than cohesive forces, the
contact angle θ lies between 0 and 90o. When adhesive
forces are smaller than cohesive forces, the contact angle θ lies between 90o and 180o.
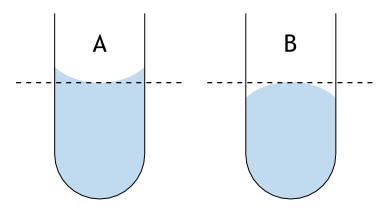
(A) A concave meniscus (example: water in glass)
(B) A convex meniscus (example: mercury in glass)
For liquid standing in a container, a meniscus forms. It
can be convex or concave. A concave meniscus indicated that the
molecules of the liquid have a stronger attraction to the material of the
container (adhesion) than to each other (cohesion). A convex
meniscus indicates the molecules have a stronger attraction to each other than
to the material of the container.
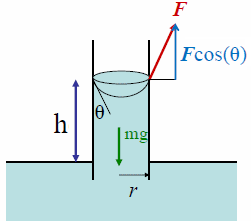
mg = (F/L) cosθ 2πr (net force = 0)
ρπr2h
g = γ cosθ 2πr (solve for h)
Adhesion and surface tension together can produce capillary
action. Capillary action occurs when the adhesion to the walls is stronger
than the cohesive forces between the liquid molecules. Adhesion of water
to the walls of a vessel results in an upward force on the liquid at the edges.
The surface tension keeps the surface intact, so the whole liquid surface is
dragged upward.
The maximum height to which the liquid will rise through
capillary action is given by
h = 2γcosθ/(ρgr).
Then the weight of the
risen liquid is balanced by the surface tension.
(See diagram on the right.)
 The surface of a liquid behaves as though it is covered by a
stretched membrane. The strength of the membrane depends on the liquid.
It is, for example, much higher for pure water than for soapy water.
Cohesive forces that act between the molecules of the liquid without
chemical bonding give rise to the surface tension. [Molecules
in liquids experience strong intermolecular attractive forces. When those forces
act between like molecules, they are referred to as cohesive forces. When the
attractive forces act between unlike molecules, they are said to be adhesive
forces.]
The surface of a liquid behaves as though it is covered by a
stretched membrane. The strength of the membrane depends on the liquid.
It is, for example, much higher for pure water than for soapy water.
Cohesive forces that act between the molecules of the liquid without
chemical bonding give rise to the surface tension. [Molecules
in liquids experience strong intermolecular attractive forces. When those forces
act between like molecules, they are referred to as cohesive forces. When the
attractive forces act between unlike molecules, they are said to be adhesive
forces.]  The surface of a liquid behaves like an elastic membrane. A surface
molecule which is displaced by a small amount is acted on by a restoring force
due to cohesive forces.
The surface of a liquid behaves like an elastic membrane. A surface
molecule which is displaced by a small amount is acted on by a restoring force
due to cohesive forces. Picture a soap bubble. The surface tension balances the outward force
due to the pressure difference between the inside and the outside air. We have two surfaces, the inner and the outer
surface of the bubble. The force from surface tension is F = 2γL =
2γ2πr = 4γπr. For the bubble to be stable and not
collapse, the pressure inside the bubble must be higher than the
pressure on the outside. The force due to the pressure difference
must balance the force from the surface tension. The force to the
pressure difference is (Pi - Po)πr2.
Picture a soap bubble. The surface tension balances the outward force
due to the pressure difference between the inside and the outside air. We have two surfaces, the inner and the outer
surface of the bubble. The force from surface tension is F = 2γL =
2γ2πr = 4γπr. For the bubble to be stable and not
collapse, the pressure inside the bubble must be higher than the
pressure on the outside. The force due to the pressure difference
must balance the force from the surface tension. The force to the
pressure difference is (Pi - Po)πr2. Detergents lower the surface tension of water. Detergent
molecules have two ends, one hydrophobic end, repelled by water and one hydrophilic end, attracted to water.
Detergents lower the surface tension of water. Detergent
molecules have two ends, one hydrophobic end, repelled by water and one hydrophilic end, attracted to water. In water detergent molecules on the surface are aligned with
their hydrophobic ends away from the surface. They break the surface and
thus lower the surface tension. Other detergent molecules are dispersed
throughout the water. Particles of organic matter are rendered soluble by
being coated with these detergent molecules. The hydrophobic ends stick to
the particles and the hydrophilic ends point outwards.
In water detergent molecules on the surface are aligned with
their hydrophobic ends away from the surface. They break the surface and
thus lower the surface tension. Other detergent molecules are dispersed
throughout the water. Particles of organic matter are rendered soluble by
being coated with these detergent molecules. The hydrophobic ends stick to
the particles and the hydrophilic ends point outwards. Wetting is the ability of liquids to form interfaces with solid surfaces. The
contact angle θ
between the liquid and the solid surface is a measure of the degree of
wetting. A smaller the contact angle and a smaller the surface
tension result in a greater the degree of wetting.
Wetting is the ability of liquids to form interfaces with solid surfaces. The
contact angle θ
between the liquid and the solid surface is a measure of the degree of
wetting. A smaller the contact angle and a smaller the surface
tension result in a greater the degree of wetting. When adhesive forces are greater than cohesive forces, the
contact angle θ lies between 0 and 90o. When adhesive
forces are smaller than cohesive forces, the contact angle θ lies between 90o and 180o.
When adhesive forces are greater than cohesive forces, the
contact angle θ lies between 0 and 90o. When adhesive
forces are smaller than cohesive forces, the contact angle θ lies between 90o and 180o.
