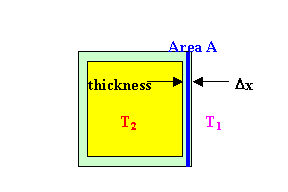
If we surround an object at temperature T2 with a layer of
material, to insulate it from its surrounding at temperature T1, then
the thermal conductivity of the surrounding
material determines how fast heat can flow through it.Heat always flows from a region of higher temperature to a region of lower temperature. It flows by conduction, convection, and radiation. Often we are interested in regulating the rate at which the thermal energy is transferred. We may want to keep an object at a temperature different from that of its surrounding for a long time by slowing down heat flow. Or we may want an object to cool down rapidly by increasing the rate at which thermal energy is transferred. In developing methods to do this effectively, we always have to consider the importance of the three different ways by which heat flows.
If we surround an object at temperature T2 with a layer of
material, to insulate it from its surrounding at temperature T1, then
the thermal conductivity of the surrounding
material determines how fast heat can flow through it.
The thermal conductivity k is defined through the equation ΔQ/Δt = -kA ΔT/Δx.
Thermal conductivities:
(kcal/sec)/(oC m)
| Aluminum | 4.9 * 10-2 |
|---|---|
| Copper | 9.2 * 10-2 |
| Steel | 1.1 * 10-2 |
| Air | 5.7 * 10-6 |
| Ice | 4 * 10-4 |
| Wood | 2 * 10-5 |
| Glass | 2 * 10-4 |
| Asbestos | 2 * 10-5 |
The unit kcal (kilocalorie) is a unit of energy.
1 kcal = 4186 J.
This equation is called the law of heat conduction. ΔQ/Δt
is the rate at which heat flows across the area A, in Joules per second
or Watts. ΔT/Δx is the change in the temperature over the distance
Δx in degrees Kelvin or Celsius per meter. It is the temperature
gradient. The thermal conductivity k is a property of the
material. The minus sign indicates that heat flows in the opposite
direction of the temperature gradient, from the high to the low temperature
side.
To minimize heat flow through a layer of material by
conduction, choose the right material, make the layer as thick as possible, and
make the surface area as small as possible.
Clothing intended to reduce heat flow
should use low-thermal conductivity materials. Clothes should be relatively
thick and trap air, since air is a poor thermal conductor. The materials
should not contain metals, since metals are good thermal conductors.
Calculate the rate of heat flow (in J/s = Watts) by conduction through a glass window 2.0 m multiplied by 3 m in area and 4 mm thick, if the inside temperature is 15o C and the outside temperature is -5o C.
Solution:
This is an enormous rate of heat flow. The next problem shows how by trapping a thin layer of air between two layer of glass we can reduce heat loss by conduction significantly.
A Thermopane window of area 6 m2 is constructed of two layers of glass, each 4 mm thick, separated by an air space of 5 mm. If the inside is at 15 oC and the outside is at -5 oC, what is the rate of heat loss through the window? The thermal conductivity of the glass is 0.84 W/(moC) and the thermal conductivity of the air is 0.0234 W/(moC).
Solution:
Heat naturally flows from a region of higher to a region of
lower temperature. In fluids a hotter region has lower density than a colder
region. Near the surface of the earth, where the gravitational acceleration
points downward, buoyancy causes the hotter fluid to rise, setting up convection
currents. The rate of heat flow depends on the heat capacity and mobility of
the fluid, i.e. how quickly heat flows into or out of the fluid and how
well the fluid circulates because of buoyancy.
Buoyancy is not always moving a fluid effectively. It fails when the hotter
fluid is above the colder fluid, when fluids experience large drag forces, or
when the geometry of the container prevents fluid flow. One can help the fluid
move and therefore enhance heat transfer by stirring the fluid. In air, wind
increases heat transfer (wind chill) by forcing convection.
Clothing can reduce convective heat transfer
by preventing fluids from circulating.
The particles that make up an object can have ordered energy and disordered energy. The temperature is a measure of this internal, disordered energy. The absolute temperature of any substance is proportional to the average kinetic energy associated with the random motion of the substance.
The velocity of particles with thermal energy is changing almost all the time. The particles are accelerating. The atoms and molecules are themselves complicated arrangements of charged particles. Accelerating charged particles produce electromagnetic radiation. The power radiated is proportional to the square of the acceleration. Higher rates of velocity change result in higher frequency (shorter wavelength) radiation.
Experimental challenges:
Ideal solution:
Use a blackbody. A blackbody is a body that absorbs all the radiation that falls onto it. It does not reflect any radiation. It reaches thermal equilibrium with its surroundings, and in thermal equilibrium emits exactly as much radiation it absorbs. It has emissivity = 1. Emissivity measures the fraction of radiative energy that is absorbed by the body.
Experimental realization:
Use the inside of a large box (oven) held at a constant temperature T. A small hole is cut in one side. Any radiation that enters through the hole bounces around inside and has little chance of ever getting out again. Eventually it gets absorbed. Radiation coming out the hole is as good a representation of the radiation from a perfect emitter.
What is observed?
The observed intensity of the radiation emitted as a function of wavelength can be described by the Planck Radiation Law.
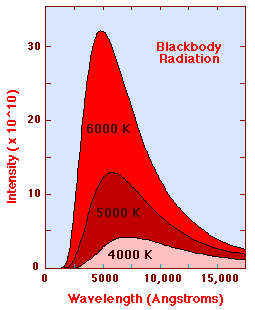The Planck Radiation Law gives the
intensity of radiation emitted by a blackbody
as a function of wavelength for a fixed temperature. The Planck law gives a
distribution, which peaks at some wavelength. The peak shifts to shorter
wavelengths for higher temperatures, and the area under the curve grows rapidly
with increasing temperature. The diagram below shows the intensity distribution
predicted by the Plank law in J/(m2s) for blackbodies at various
temperature.
The Wien law and the Stefan-Boltzmann Law can be derived from the Planck Radiation Law.
The Wien Law gives the
wavelength of the peak of the radiation distribution,
λmax = 3*106/T.
Here λ is measured
in units of nanometer = 10-9 m and T is in Kelvin.
The Wien law can be the basis of a
non-contact measurement of the temperature of a hot object.
One measures the wavelength distribution of the radiation emitted by
the object and from the peak infers the temperature.
External link: Disappearing-filament pyrometer
The Wien law explains the shift of the peak to shorter
wavelengths as the temperature increases.
The Stefan-Boltzmann Law
gives the total energy being emitted at all wavelengths by the body.
Radiated power = emissivity * σ * T4 * Area
Here σ is the Stefan-Boltzmann constant,
= 5.67*10-8 W/(m2K4) and the
temperature is measured in Kelvin.
The Stefan-Boltzmann
law explains the growth in the height of the curve as the
temperature increases. This growth is very abrupt, since it
varies as the fourth power of the temperature.
External link: PhET Simulation: Blackbody Spectrum
The emissivity of an object is the ratio of the radiative power emitted by that object at temperature T to the radiative power emitted by a blackbody of the same shape and temperature T. It is also equal to the fraction of the incoming blackbody radiation at that temperature that is not reflected but absorbed by the object. The emissivity of objects is a function of the temperature T and can be quite different for visible and infrared radiation.
The emissivity of an object for radiation emitted by high temperature sources (visible light) is easily determined by just looking at the object. A dark surface has a high-temperature emissivity near 1, while a white or shiny surface has a high-temperature emissivity near 0. Light-colored or reflective objects have low emissivity. They do absorb a smaller percentage of the incoming visible radiation than do dark objects, and also emit radiation less readily.
One cannot "see" the emissivity of an object for radiation emitted by low temperature sources (infrared light). Most materials have a low-temperature emissivity near 1, but conducting (metallic) surfaces can have a low-temperature emissivity near 0. If you wrap a hot object in reflective aluminum foil, then the foil reflects most of the radiation emitted by the object back onto the object. Heat loss by radiation is thus slowed down.
To reduce radiative heat transfer, use low-emissivity surfaces and allow exterior surfaces to reach the ambient temperature.
A burning log is an approximate black-body object with a surface area of 0.25 m2 and a temperature of 800 oC. How much power does it emit as thermal radiation?
Solution:
Compare the rate R1 at which cup of water at 50oC radiates energy with he rate R2 at which cup of water at 100oC radiates energy/
Solution: