 What is the relationship between temperature and pressure?
What is the relationship between temperature and pressure?The particles that make up an object can have ordered energy and disordered energy. The kinetic energy of an object as a whole due to its motion with velocity v with respect to an observer is an example of ordered energy. The kinetic energy of individual atoms, when they are randomly vibrating about their equilibrium position, is an example of disordered energy. Thermal energy is disordered energy. The temperature is a measure of this internal, disordered energy.
The absolute temperature of any substance is proportional to the average kinetic energy associated with the random motion of the atoms or molecules that make up the substance.
In a gas, the individual atoms and molecules are moving randomly. The absolute temperature T of the gas is proportional to the average translational kinetic energy of a gas atom or molecule, ½m<v2>. In SI units, the proportional constant is (3/2)kB, where kB = 1.381*10-23 J/K or 1.381*10-23 Pa m3/K is called the Boltzmann constant.
½m<v2> = (3/2)kBT
In a solid, the atoms can move randomly about their equilibrium positions.
In addition, the solid as a whole can move with a given velocity and have
ordered kinetic energy. Only the kinetic energy associated with the random
motion of the atoms is proportional to the absolute temperature of the solid.
In ideal gases the disordered energy is all kinetic energy, in molecular
gases and solids it is a combination of kinetic and potential energy. If
we model the atoms in a solid as being held together by tiny springs, then the
random internal energy of each atom constantly switches between kinetic energy
and elastic potential energy.
In classical physics, zero absolute temperature means zero kinetic energy associated with random motion. The atoms in a substance do not move with respect to each other. (The uncertainty principle in quantum mechanics requires that there is some zero-point energy.) Room temperature is not close to absolute zero temperature. At room temperature the atoms and molecules of all substances have random motion.
In SI units the scale of absolute temperature is Kelvin (K). The Kelvin scale is identical to the Celsius (oC) scale, except it is shifted so that 0 degree Celsius equals 273.15 K. We have
temperature in oC = temperature in K - 273.15.
To convert to temperature in Fahrenheit we can use
temperature in oF = (9/5) * temperature in oC + 32.
Average atomic and molecular speeds (vrms = <v2>½ = root mean square speed) are large, even at low temperatures. What is vrms for helium atoms at 5.00 K, just one degree above helium's liquefaction temperature?
Solution:
The root-mean-square speed of the atoms or molecule with mass m is vrms = <v2>½ = (3kBT/m)½.
Liquid nitrogen has a boiling point of -195.81 oC at atmospheric
pressure. Express this temperature in
(a) degrees Fahrenheit and
(b) Kelvin.
Solution:
One of the hottest temperatures ever recorded on the surface of Earth was
134 oF in Death Valley, CA.
(a) What is this temperature in oC?
(b) What is this temperature in Kelvin?
Solution:
(a) At what temperature do the Fahrenheit and Celsius scales have the same
numerical value?
(b) At what temperature do the Fahrenheit and Kelvin scales have the same
numerical value?
Solution:
 What is the relationship between temperature and pressure?
What is the relationship between temperature and pressure?Assume we have a collection of gas molecules in gravity-free space in a container with volume V at absolute temperature T.
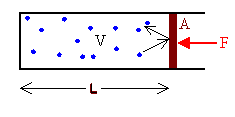
Then each molecule moves along with constant velocity in a straight line, until it hits another molecule, or a container wall. A collision between two molecules is similar to a collision between two balls. The molecules exchange momentum, but the total momentum of the two molecules is conserved. When a molecule hits a wall, it bounces back. Its momentum changes. To change the molecule's momentum, the wall must exert a force on the molecule. Newton's third law tells us that the molecule exerts a force on the wall. The greater the number of molecules hitting a wall, the greater is the force on the wall. In a container with different size walls, the bigger walls will receive more hits than the smaller walls and therefore experience a greater force. The pressure in the container is the magnitude of the normal force F on a wall divided by the surface area A of the wall.
P = F/A
 The faster the molecules move in the container, the greater is the change in
momentum when they bounce off a wall, and the more often do they hit the walls.
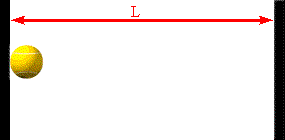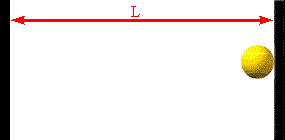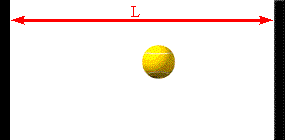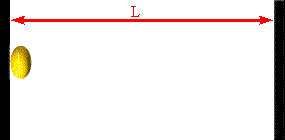
Assume a molecule moves horizontally with speed |vx| back and forth
between two infinitely-massive walls, which are a distance L apart. When
it hits the right wall its momentum changes from p1 = +m|vx|
to p2 = -m|vx|. The change in the molecule's
momentum is Δpmol = p2
- p1 = -2m|vx|. The time interval between successive
hits on the right wall is Δt = 2L/|vx|. So the average force
the wall exerts on this molecule is Fmol
= Δpmol/Δt = -2m|vx|/(2L/|vx|) = -mvx2/L.
By Newton's third law, the average force that the molecule exerts on the wall is
Fwall
= mvx2/L, it is proportional to the square of the
speed of the molecule or its kinetic energy.
The faster the molecules move in the container, the greater is the change in
momentum when they bounce off a wall, and the more often do they hit the walls.
Assume a molecule moves horizontally with speed |vx| back and forth
between two infinitely-massive walls, which are a distance L apart. When
it hits the right wall its momentum changes from p1 = +m|vx|
to p2 = -m|vx|. The change in the molecule's
momentum is Δpmol = p2
- p1 = -2m|vx|. The time interval between successive
hits on the right wall is Δt = 2L/|vx|. So the average force
the wall exerts on this molecule is Fmol
= Δpmol/Δt = -2m|vx|/(2L/|vx|) = -mvx2/L.
By Newton's third law, the average force that the molecule exerts on the wall is
Fwall
= mvx2/L, it is proportional to the square of the
speed of the molecule or its kinetic energy.
Assume that there are N molecules in the volume V, moving horizontally with
speed |vx|. Not all the molecules have the same
kinetic energy. The force
exerted by the molecules on the walls of a container is therefore F = Nm<vx2>/L,
where <vx2> is the average value of vx2.
The pressure is P = F/A = Nm<vx2>/V,
since L*A = V. With ρparticle = N/V we have
P = F/A = ρparticlemvx2.
There is nothing special about the x-direction. The atoms can move up and down, back and forth, in and out. The average velocity components in all directions are all going to be equal to each other.
<vx2> = <vy2> = <vz2>.
They are each equal to one-third of their sum, which is the square of the magnitude of the average velocity.
<v2> = <vx2> + <vy2>
+ <vz2>.
<vx2> = (1/3)<v2>.
We may therefore write
P = (1/3)ρparticlem<v2> = (2/3)ρparticle(m<v2>/2)
This equation relates the pressure to the kinetic energy of the atoms or molecules, since m<v2>/2 is the kinetic energy of the center-of-mass or translational motion of an atom or molecule. Using ½m<v2> = (3/2)kBT and ρparticle = N/V from above we therefore find that
PV = (2/3)N(m<v2>/2)
PV = NkBT.
The pressure in a container is proportional to the average kinetic energy of the molecules and therefore to the absolute temperature T of the gas.
If all the molecules in a container would be at rest, their kinetic energy would be zero and the pressure would be zero.
PV = NkBT is called the ideal gas law. Most real gases at ordinary temperatures and pressures obey the ideal gas law. The ideal gas law can be rewritten as
PV = nNAkBT = nRT.
Here n is the number of moles of the gaseous substance, NA is Avogadro's number, NA = 6.022*1023 molecules/mol, and R = NAkB is a constant, called the universal gas constant, R = 8.31 J/(mol K).
The number of moles n is given by n = m/M where m is the average mass of the gas particles in the volume and M is the molar mass of the gas.
In the 17th and 18th century experiment with gases at very low temperature and pressures revealed three relations that are generalized by the ideal gas law.
The ideal gas law holds well for real gases at low densities and pressures, such as atmospheric density and pressure. If we use T = 0 oC = 273 K and P = 1 atm, then we find that one mole of gas occupies a volume of 22.4 liters. One mole of gas contains NA gas particles. For all low density gases, NA gas particles occupy 22.4 liters at T = 273K and P = 1 atm.
Nothing in the ideal gas law depends on the nature of the gas particles. The value of PV/T depends only on the number of gas particles and a universal constant.
Note: In all gas laws T denote the absolute temperature, measured in Kelvin in SI units.
The particle density of atmospheric air at 273.15 K at sea level is 2.687*1025/m3. Calculate the pressure P.
Solution:
If a helium-filled balloon initially at room temperature is placed in a freezer, will its volume increase, decrease, or remain the same?
Solution:
External link: Balloons in Liquid Nitrogen (Youtube)