Optical instruments
Do you wear glasses? Are you farsighted or nearsighted?
What do you see when you hold your glasses or someone else's glasses far away from your face? Look
through your or another student's glasses as you move them towards or away from a
printed page. Describe what you see.
In the session you will explore image formation. You
will determine the focal length of a thin lens and observe aberrations.
You will then build a simple Keplerian
telescope and a simple compound microscope.
Equipment:
- Diffuse reflecting screen
- Converging lenses
- Lamp
- Optical track
- Ruler
Open a Microsoft Word document to keep a log of your procedures,
results and discussions. This log will become your lab report. Address the
points highlighted in blue. Answer all questions.
Experiment 1
 Determine the focal length of a converging lens and observe coma.
Determine the focal length of a converging lens and observe coma.
- Mount the diffuse reflecting screen onto the optical rail.
- Turn on the laser and shine it onto the diffuse reflecting screen from the
side as shown in the picture to the right.
You should see a red spot.
The spot should be above the center of the post, ~ 27 - 28 cm above
the table. This height will allow you to align the other optical
components. Alignment is critical for all optics experiments.
You will have to set the laser on a thick book to get it to the right height.
-
 You will have to measure distances between optical components.
If mounted correctly, the center of all components will be located
over the centers of the mounts. You can therefore determine the distances between the components by measuring the distances
between the edges of the mounts.
You will have to measure distances between optical components.
If mounted correctly, the center of all components will be located
over the centers of the mounts. You can therefore determine the distances between the components by measuring the distances
between the edges of the mounts.
To make distance determinations convenient, put the edge of the screen mount at 10 cm or 20 cm.
-
 Place the 10 cm focal length lens in its holder on the track approximately 10 cm away from the screen.
Place the 10 cm focal length lens in its holder on the track approximately 10 cm away from the screen.
- Make sure the red spot and the center of the lens are at the same height, and, as you look along the track, the spot is aligned with the middle of the lens.
- This red spot will be your object. If this object is located in the
focal plane of the lens, then light from the object will leave the
lens as a parallel beam. If a parallel beam is incident on the
lens, it will come to a focus in the focal plane. This is
called the principle of ray reversibility.
- Place the mirror approximately 25 cm away from the screen. Make sure
the center of the mirror is at the same height as the red spot and
the center of the lens. The mirror will reflect a parallel
beam of the light and focus it back to a small spot.
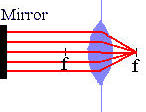
- Move the lens until you obtain the smallest reflected spot possible. Adjust the
mirror so that the reflected spot appears close to the object spot.
- Measure the distance from the center of the lens to the screen (in units of cm). That
distance is your measured focal length of the lens. Record your measured focal length in your log.
- Check if moving the mirror a small distance along the track changes anything.
 Rotate the lens approximately 20 degrees about the vertical axis in
either direction. Describe what happens to the reflected spot. You should observe a lens aberration
called "coma". It is observed when the light rays make large
angles with the symmetry axis of spherical mirrors or lenses.
Rotate the lens approximately 20 degrees about the vertical axis in
either direction. Describe what happens to the reflected spot. You should observe a lens aberration
called "coma". It is observed when the light rays make large
angles with the symmetry axis of spherical mirrors or lenses.
Experiment 2
Observe the formation of a real image using a converging lens.
-
 Turn off the laser, remove the mirror, and place the lamp on the track as shown.
Make sure the lamp and the lens are at the same height.
Place the lamp 50 cm away from the screen.
Turn off the laser, remove the mirror, and place the lamp on the track as shown.
Make sure the lamp and the lens are at the same height.
Place the lamp 50 cm away from the screen.

- A cross pattern is cut into the lamp cover. Let the cross
face the lens.
-
 Move the 10 cm focal length lens along
the track until you see one of the sharpest images of the cross on the
screen. Measure the object distance xo from the cross on
the lamp to the center of the lens and the image distance xi
from the center of the lens to the image on the screen and record
these distances in table 1.
Move the 10 cm focal length lens along
the track until you see one of the sharpest images of the cross on the
screen. Measure the object distance xo from the cross on
the lamp to the center of the lens and the image distance xi
from the center of the lens to the image on the screen and record
these distances in table 1.
- Measure the height of the cross ho and the height of
its image hi and record these heights in table 1.
- Note if the image is upright or inverted.
- Using the lens equation,
1/xo + 1/xi = 1/f
of f = xoxi/(xo + xi),
calculate the focal length and record it in table 1.
- Using the equation M = -xi/xo calculate the magnification
and record it in table 1.
- There are two locations for the lens where you get a sharp
image. Move the lens until you find the second location.
Repeat the measurements and calculations from above and record them in table 1.
- Now move the lamp 45 cm away from the screen. Move the
lens along the track until you see the sharpest images of the cross on the
screen. Repeat the measurements and
calculations from above and record them in table 1.
- Rotate the lens approximately 20 degrees about the vertical axis in either direction.
Describe what happens to the image. Are the vertical and horizontal lines still
in focus at the same place? If not, move the screen to put either the vertical
or the horizontal line of the cross in focus. You should observe a lens
aberration called "astigmatism".
- To observe distortion, hold the f = 6
cm convex lens like a magnifying glass in your hand. Look at
various images of parallel lines on a piece of millimeter paper. Hold
the lens at various distances from the paper creating both virtual and real
images. Describe the distortions you can
observe.
Table 1
screen-lamp
distance
|
measured xo
|
measured xi
|
calculated focal length:
f = xoxi/(xo + xi) |
measured ho
|
measured hi
|
measured magnification:
M = -hi/ho |
calculated magnification:
M = -xi/xo |
| 50 cm (1) |
|
|
|
|
|
|
|
| 50 cm (2) |
|
|
|
|
|
|
|
| 45 cm (1) |
|
|
|
|
|
|
|
| 45 cm (2) |
|
|
|
|
|
|
|
For the measurements of experiment 1 and 2 answer the following questions.
- Paste the table into your Word document.
- Do the three measurements from experiment 2
yield the same focal length within experimental uncertainties?
Explain how the measurements could be "off", given the equipment you used.
- Does the focal length obtained in experiment 1
agree with the focal length obtained in experiment 2 within experimental
uncertainties?
- Do the measured and the calculated magnification agree within
experimental uncertainties? Explain how the measurements could be
"off".
- Did you observe inverted or an upright images?
- Did you observe aberrations?
Experiment 3
Your lens is a bi-convex lens. Both sides are curved. While most of the light from the lamp is
transmitted through the lens, some light will be reflected from the front
surface, and some from the back
surface.
- Remove the screen.
- With the lens approximately 25 cm away from the lamp, look into the lens
from the lamp side.
- Describe your observations. Move
the lens back and force and try to "touch" the images you see with your
finger. Are they in front or behind the lens?
Are they real or virtual?
Experiment 4
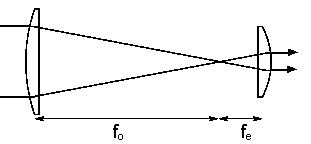 Build a Keplerian telescope with a magnifying power of ~3.1.
Build a Keplerian telescope with a magnifying power of ~3.1.
Use the 12.5 cm focal length lens for the objective and the 4 cm focal length lens for the eyepiece.
Let the center to center
distance between the lenses be ~16.5 cm.
 Build your telescope on the optical rail. (Remove
the lamp.) Make
sure the center of both lenses is at the same height.
You can then easily slide the components along the rail without destroying the alignment.
Fix the objective to the rail. Place your eye approximately 5 cm away from the
eyepiece and move the eyepiece back and forth until you can see a sharp
image of a distant target. Look at the most distant target you can find
considering the size limitations of the laboratory.
Build your telescope on the optical rail. (Remove
the lamp.) Make
sure the center of both lenses is at the same height.
You can then easily slide the components along the rail without destroying the alignment.
Fix the objective to the rail. Place your eye approximately 5 cm away from the
eyepiece and move the eyepiece back and forth until you can see a sharp
image of a distant target. Look at the most distant target you can find
considering the size limitations of the laboratory.
Record in your log:
- distance from objective to target
- actual distance between objective and
eyepiece when you see the sharpest image
 Evaluate the performance of your telescope.
Evaluate the performance of your telescope.
- Can you see features of the target through the telescope that you cannot see when you
view the target from the same distance with the naked eye?
- Is the image upright or inverted?
- How does your field of view (the biggest angle in your
view away from the center line from your eye to the target) change when you
switch from looking at the target with your naked eye to looking through the telescope?
- Given your target distance, is the actual
distance between objective and eyepiece when you see the sharpest
image different from 16.5 cm? (16.5 cm is the nominal "best
distance" for viewing very distant objects.)
Experiment 5
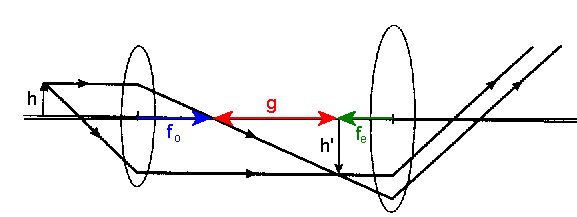
- Design a simple compound microscope with a tube length g of 16 cm, an objective with focal length fo
= 6 cm, and an eyepiece with focal length 12.5 cm.
- The magnifying power of this microscope is MP = -(g/fo)(25
cm/fe) ~ 5.3.
16 cm is the most common tube length for laboratory microscopes.
-
 Build your microscope on the optical rail.
Build your microscope on the optical rail.
- Let the center to center distance between the lenses be 34.5 cm.
Fix this distance by tightening the screws on the post holders.
- Place the target ~8.5 cm in front of the objective.
-
 Place your eye as close as possible to the eyepiece and move the
object back and forth until you can see a sharp image of the object.
Place your eye as close as possible to the eyepiece and move the
object back and forth until you can see a sharp image of the object.
- Evaluate the performance of your compound
microscope by
examining a tiny object of your choice.
- What is the best target-objective distance
for a fixed objective-eyepiece distance? Does it depend on who is
looking through the microscope? Why or why not?
Convert your log into a lab report.
See the grading scheme for all lab
reports.
Name:
E-mail address:
Laboratory 8 Report
- In one or two sentences, state the goal of this lab.
- Make sure you completed the entire lab and answered all parts. Make
sure you show your work and inserted and properly labeled relevant tables
and plots.
- Add a reflection at the end of your report in a short essay format.
Save your Word document (your name_lab7.docx), go to Canvas, Assignments, Lab
8, and submit your document.
 Determine the focal length of a converging lens and observe coma.
Determine the focal length of a converging lens and observe coma. Determine the focal length of a converging lens and observe coma.
Determine the focal length of a converging lens and observe coma. You will have to measure distances between optical components.
If mounted correctly, the center of all components will be located
over the centers of the mounts. You can therefore determine the distances between the components by measuring the distances
between the edges of the mounts.
You will have to measure distances between optical components.
If mounted correctly, the center of all components will be located
over the centers of the mounts. You can therefore determine the distances between the components by measuring the distances
between the edges of the mounts.  Place the 10 cm focal length lens in its holder on the track approximately 10 cm away from the screen.
Place the 10 cm focal length lens in its holder on the track approximately 10 cm away from the screen.
 Rotate the lens approximately 20 degrees about the vertical axis in
either direction. Describe what happens to the reflected spot. You should observe a lens aberration
called "coma". It is observed when the light rays make large
angles with the symmetry axis of spherical mirrors or lenses.
Rotate the lens approximately 20 degrees about the vertical axis in
either direction. Describe what happens to the reflected spot. You should observe a lens aberration
called "coma". It is observed when the light rays make large
angles with the symmetry axis of spherical mirrors or lenses. Turn off the laser, remove the mirror, and place the lamp on the track as shown.
Make sure the lamp and the lens are at the same height.
Place the lamp 50 cm away from the screen.
Turn off the laser, remove the mirror, and place the lamp on the track as shown.
Make sure the lamp and the lens are at the same height.
Place the lamp 50 cm away from the screen.
 Move the 10 cm focal length lens along
the track until you see one of the sharpest images of the cross on the
screen. Measure the object distance xo from the cross on
the lamp to the center of the lens and the image distance xi
from the center of the lens to the image on the screen and record
these distances in table 1.
Move the 10 cm focal length lens along
the track until you see one of the sharpest images of the cross on the
screen. Measure the object distance xo from the cross on
the lamp to the center of the lens and the image distance xi
from the center of the lens to the image on the screen and record
these distances in table 1.  Build a Keplerian telescope with a magnifying power of ~3.1.
Build a Keplerian telescope with a magnifying power of ~3.1.
 Build your telescope on the optical rail. (Remove
the lamp.) Make
sure the center of both lenses is at the same height.
You can then easily slide the components along the rail without destroying the alignment.
Fix the objective to the rail. Place your eye approximately 5 cm away from the
eyepiece and move the eyepiece back and forth until you can see a sharp
image of a distant target. Look at the most distant target you can find
considering the size limitations of the laboratory.
Build your telescope on the optical rail. (Remove
the lamp.) Make
sure the center of both lenses is at the same height.
You can then easily slide the components along the rail without destroying the alignment.
Fix the objective to the rail. Place your eye approximately 5 cm away from the
eyepiece and move the eyepiece back and forth until you can see a sharp
image of a distant target. Look at the most distant target you can find
considering the size limitations of the laboratory. Evaluate the performance of your telescope.
Evaluate the performance of your telescope. 
 Build your microscope on the optical rail.
Build your microscope on the optical rail. Place your eye as close as possible to the eyepiece and move the
object back and forth until you can see a sharp image of the object.
Place your eye as close as possible to the eyepiece and move the
object back and forth until you can see a sharp image of the object.