Experiment 2

In the PASCO e/m apparatus a beam of electrons is accelerated through a known potential difference, so the kinetic energy and therefore the velocity of the electrons is known.  A pair of Helmholtz coils can produce a uniform magnetic field at right angles to the electron beam.  This magnetic field then deflects the electron beam in a circular path.  A unique feature of the e/m tube is that the socket rotates, allowing the electron beam to be oriented at any angle (from 0-90 degrees) with respect to the magnetic field produced by the Helmholtz coils.  The vector nature of the magnetic force on moving charged particles can therefore be explored.  A small permanent magnet can also be used to deflect the electron beam.

The e/m Tube

The e/m tube is filled with helium at a pressure of 10^-2 mm Hg.  It contains an electron gun and deflection plates.

The electron beam leaves a visible trail in the tube, because some of the electrons collide with helium atoms.  The atoms are excited and then radiate visible light.  The electron gun is shown in the figure below.
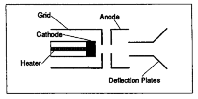
The heater heats the cathode, which emits electrons.  The electrons are accelerated by a potential difference between the cathode and the anode.  A grid is held positive with respect to the cathode and negative with respect to the anode.  It helps to focus the electron beam.

The Helmholtz Coils

The radius of the coils is equal to their separation.   This geometry provides a highly uniform magnetic field near the center of the coils.   The Helmholtz coils of the e/m apparatus have a radius and a separation of 15 cm.  Each coil has 130 turns.  The magnetic field B produced by the coils is proportional to the current I through the coils times 7.8*10^-4 T/A.  It is perpendicular to the plane of the coils.

B = (7.8*10^-4 T/A)*I.

Cloth Hood

The hood can be placed over the top of the e/m apparatus so the experiment can be performed in a lighted room.

Mirrored Scale

A mirrored scale is attached to the back of the rear Helmholtz coil.  It is illuminated when the heater of the electron gun is powered.  By lining the electron beam up with its image in the mirrored scale, the radius of the beam path can be measured without parallax error.

Part I:  Measuring e/m

Procedure:

• Make sure both power supplies are turned off.
• Place the hood over the e/m apparatus.
• Flip the toggle switch up to the e/m MEASURE position.
• Connect the power supplies to the front panel of the e/m apparatus, as shown in the figure below.  The Low Voltage supply is on the bottom, the High Voltage supply is on the top.  Before you turn on the Low Voltage supply, turn the voltage knob all the way down and the current knob all the way up.  You can then adjust the output voltage with the voltage knob.
  

  

   

  

• Turn on and adjust the power supplies to the following levels:
  • High Voltage supply:  Electron Gun Heater: 6 VAC
    • CAUTION: The voltage to the heater of the electron gun should NEVER exceed 6.3V.  Higher voltages will burn out the filament and destroy the e/m tube.
  • High Voltage supply:  Acceleration potential: 150 to 300 VDC 
    • Do not exceed 300 V.
  • Low Voltage supply:  Helmholtz Coils: 6 - 9 VDC
• Wait several minutes for the cathode to heat up.  When it does, you will see the electron beam emerge from the electron gun.
• Slowly turn the current adjust knob for the Helmholtz coils on the PASCO e/m apparatus clockwise.  Watch the ammeter of the Low Voltage supply and take care that the current does not exceed 2 A.  The path of the electron beam will be curved by the field from the Helmholtz coils. Check that the electron beam's path is parallel to the Helmholtz coils. 
  • If it is not, turn the tube until it is.  Do not take the tube out of its socket.  As you rotate the tube, the socket will turn.
• Adjust the Helmholtz coil current and the focus, so that you can see the electron path as a a complete, well defined circle.  Carefully read the current to the Helmholtz coils from the current readout of the Low Voltage supply and the acceleration voltage from voltage readout of the High Voltage supply.  Record the values in the first two columns of the table below.  Calculate the magnetic field.

• Carefully measure the radius of the circular path of the electron beam.  Look through the tube at the electron beam.  To avoid parallax errors, move your head to align the electron beam with the reflection of the beam that you can see on the mirrored scale.  Measure the radius of the path as you see it on both sides of the scale, then average the results.  Record your result in the table in units of meter.
• Calculate e/m (in units of C/kg) from the measured values in your table.

Review:  Analysis of the e/m measurement

The magnetic force F_m acting on a charged particle of charge q moving with velocity v in a magnetic field B is given by the equation
F_m = qv × B. 
Since the electron beam in this experiment is perpendicular to the magnetic field, we have the following equation relating the magnitudes F_m, q, v, and B.
F_m = qvB.
The electron is moving in a circular path of radius r, with the magnetic force being equal to the centripetal force mv²/r.  We therefore have
qvB = mv²/r or q/m = v/Br.
We denote the magnitude of the charge q of the electron by e and therefore have
e/m = v/Br.
The electrons are accelerated through the accelerating potential V, gaining kinetic energy equal to their charge times the accelerating potential. Therefore eV = ½mv².  The velocity of the electrons therefore is v = (2eV/m)^½.  Inserting this expression for v in the equation above and squaring both sides we obtain
e/m = 2V/(Br)².

Paste your table into your log.  Calculate e/m from the accepted values of the electron's charge and mass.  Does the value of e/m from your experiment agree with the calculated value?  Given your experimental procedure, how close do you expect them to agree?

Part II: Electrons moving in a magnetic field

Procedure:

The socket for the e/m tube is designed so that the tube can be rotated through 90 degrees.  The tube can therefore be oriented so it is at any angle, from 0 - 90 degrees, with respect to the magnetic field from the Helmholtz coils.  By setting up the equipment as for measuring e/m, you can rotate the tube and study how the beam deflection is affected.

• Describe your observations as you rotate the tube.
• Describe what happens when you change the current to the Helmholtz coils.
• Describe what happens when you change the accelerating voltage.

Instead of using the Helmholtz coils to bend the electron beam, you can use a permanent magnet to show the effect of a magnetic field on the electron beam.  Provide the following power to the e/m apparatus:

• Electron gun heater: 6 VAC
• Acceleration potential: 300 VDC
• Helmholtz coil current: 0
  • When the electron beam appears, use a permanent magnet to bend the beam.
  • Describe your observations as you bring the north pole of your magnet close to the beam.
  • Describe your observations as you bring the south pole of your magnet close to the beam.