Fields
 A field
is a way of explaining action at a distance. Massive particles
attract each other. How do they do this, if they are not in contact with
each other? We say that massive particles produce gravitational fields.
A field is a condition in space that can be probed. Massive
particle are also the probes that detect a gravitational field. A
gravitational field exerts a force on massive particles. The magnitude of the
gravitational field produced by a massive object at a point
P is the gravitational force per unit mass it exerts on another massive
object located at that point. The direction of the gravitational field is
the direction of that force. We calculate the gravitation field
produced by a mass distribution using Newton's law of gravitation.
A field
is a way of explaining action at a distance. Massive particles
attract each other. How do they do this, if they are not in contact with
each other? We say that massive particles produce gravitational fields.
A field is a condition in space that can be probed. Massive
particle are also the probes that detect a gravitational field. A
gravitational field exerts a force on massive particles. The magnitude of the
gravitational field produced by a massive object at a point
P is the gravitational force per unit mass it exerts on another massive
object located at that point. The direction of the gravitational field is
the direction of that force. We calculate the gravitation field
produced by a mass distribution using Newton's law of gravitation.
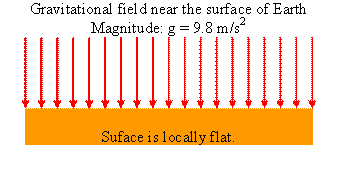
The magnitude of the gravitational force near the surface of Earth is F = mg,
the gravitational field has magnitude F/m = g. Its direction is downward.
Charged particles attract or repel each other, even when not in contact with
each other. We say that charged particles produce electric fields.
Charged particles are also the probes that detect an electric field. An
electric field exerts a force on charged particles. The magnitude of the
electric field E produced by a
charged particle at a point P is the electric force per unit positive charge
it exerts on another charged particle located at that point. The direction of
the electric field is the direction of that force on a positive charge.
The actual force on a particle with charge q is given by F = qE.
It points in the opposite direction of the electric field E for a
negative charge. We calculate the electric field produced by a
charge distribution using a set of equations called Maxwell's
equations.
In the presence of many other charges, a charge q is acted on by a net force
F, which is the vector sum of the forces due to all the other charges.
The electric field due to all the other charges at the position of the charge q
is E = F/q, i.e. it is the vector sum of the electric fields
produce by all the other charges. To measure the electric field
E at a point P due
to a collection of charges, we can bring a small positive charge q to the point
P and measure the force on this test charge. The test charge must be
small, because it interacts with the other charges, and we want this interaction
to be small. We divide the force on the test charge by the magnitude of
the test charge to obtain the field.
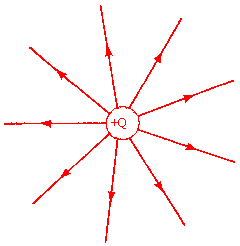 Consider a
point charge Q located at the origin.
Consider a
point charge Q located at the origin.
The force on a test charge q at position r is
F = (keQq/r2)
(r/r).
The electric field produced by Q is
E = F/q = (keQ/r2) (r/r).
If Q is positive, then the electric field points radially away from the charge.
The electric field decreases
with distance as 1/(distance)2.
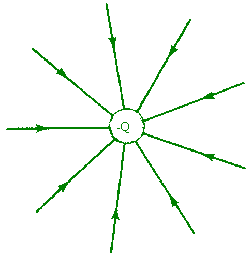 If
Q is negative, then the electric field points radially towards the charge.
If
Q is negative, then the electric field points radially towards the charge.
The electric field decreases with distance as 1/(distance)2.
We obtain the electric field due to a collection of charges using the
principle of superposition.
E = E(Q1) + E(Q2) +
E(Q3)
+ ... .
Field lines
Field lines were introduced by Michael Faraday to help visualize the
direction and magnitude of the electric field. The direction of the field at any
point is given by the direction of a line tangent to the field line, while the magnitude of the
field is given qualitatively by the density of field lines. The field lines
converge at the position of a point charge. Near a point charge their density
becomes very large. The magnitude of the field and the density of the field
lines scale as the inverse of the distance squared.
Field lines start on positive charges and end on negative charges.
Rules for drawing field lines:
- Electric field lines begin on positive charges and end on negative
charges, or at infinity.
- Lines are drawn symmetrically leaving or entering a charge.
- The number of lines entering or leaving a charge is proportional to the
magnitude of the charge.
- The density of lines at any point (the number of lines per unit length
perpendicular to the lines themselves) is proportional to the field
magnitude at that point.
- At large distances from a system of charges, the field lines are equally
spaced and radial as if they came from a single point charge equal in
magnitude to the net charge on the system (presuming there is a net charge).
- No two field lines can cross, since the field magnitude and direction
must be unique.
 Examples:
Examples:
The field lines of an electric dipole,
i.e. a positive and a negative charge of equal magnitude, separated by a
distance d.
The electric field decreases
with distance as 1/(distance)3, much faster than the field of a point charge.
Polar molecules do not have a net charge, but the centers of the positive and
negative charge do not coincide. Such molecules produce a dipole field and
interact via the electrostatic force with their neighbors.
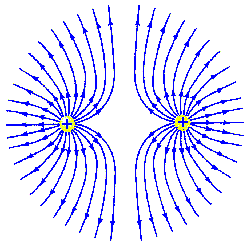 The
field lines of two positive charges of equal magnitude separated by a
distance d.
The
field lines of two positive charges of equal magnitude separated by a
distance d.
The electric field decreases with distance as 1/(distance)2.
Example:
 Every water molecule (H2O)
consists of one oxygen atom and
two hydrogen atoms. A water molecule has no net charge because the
number of positively charged protons equals the number of negatively
charged electrons in each atom. In the water molecule, each hydrogen
atom is bound to the oxygen atom by a covalent
bond. The hydrogen atom and the oxygen atom share an
electron, which has a slightly higher probability to be closer to the
oxygen atom than to the hydrogen atom. This results in a polar molecule, in which the
oxygen
"side" of the molecule has a slight negative charge, while the hydrogen
"sides" have a slight positive charge. Because water is a polar
molecule it dissolves many inorganic and organic materials. Organisms
can build macromolecules to attract or repel water as needed simply by
varying the charge on side chains.
Every water molecule (H2O)
consists of one oxygen atom and
two hydrogen atoms. A water molecule has no net charge because the
number of positively charged protons equals the number of negatively
charged electrons in each atom. In the water molecule, each hydrogen
atom is bound to the oxygen atom by a covalent
bond. The hydrogen atom and the oxygen atom share an
electron, which has a slightly higher probability to be closer to the
oxygen atom than to the hydrogen atom. This results in a polar molecule, in which the
oxygen
"side" of the molecule has a slight negative charge, while the hydrogen
"sides" have a slight positive charge. Because water is a polar
molecule it dissolves many inorganic and organic materials. Organisms
can build macromolecules to attract or repel water as needed simply by
varying the charge on side chains.
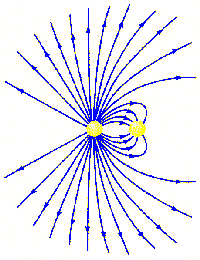 Problem:
Problem:
The figure on the right shows the electric field lines for a system of two point
charges.
(a) What are the relative magnitudes of the charges?
(b) What are the signs of the charges?
Solution:
- Reasoning:
Rules for drawing field lines:
Electric field lines begin on positive charges and end on negative
charges, or at infinity.
The number of lines entering or leaving a charge is proportional to the
magnitude of the charge.
- Details:
(a) There are 32 lines coming from the charge on the left, while there
are 8 converging on that on the right. Thus, the magnitude of the
charge on the left is 4 times
larger than the magnitude of the charge on the right.
(b) The charge on the left is positive, the charge on the right is negative.
Electric field near an infinite plane of charge
The field of an infinite planar charge distribution is uniform. It does
not decrease with distance. The field has magnitude E = σ/(2ε0)
and points away from a positively charged plane and towards a negatively charged
plane. ΔQ/ΔA = σ is the charge per unit area on the plane. Of course, there are no infinite sheets of
charge. But E = σ/(2ε0) is a good approximation to the field near a
finite-size plane of charge, as long as the dimensions of the plane are much
larger than the distance away from the plane where we want to know the
field.
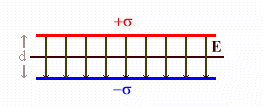 The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is
The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is
E1 = σ/2ε0, x > d/2, E1 =
-σ/2ε0, x < d/2.
The field due to the lower plane of charge is
E2 = σ/2ε0, x < -d/2, E2 =
-σ/2ε0, x > -d/2.
The total field in the region x < -d/2 is E = E1 + E2
= -σ/2ε0 + σ/2ε0 = 0.
Similarly, the total field in the region
x > d/2 is zero.
In the region between -d/2 and +d/2 the total field is is
E = E1 + E2 = -σ/2ε0 - σ/2ε0
= -σ/ε0.
The fields add to yield a uniform field between the planes, but they
precisely cancel outside the planes to give zero net field outside. Between the
planes the field points from the positive towards the negative plane. This is
the common configuration of a parallel plate
capacitor.
Please watch
this
video clip that helps you "see" the electric field!
Embedded Question 3
Which of the diagrams below is not a valid field line diagram, and why?
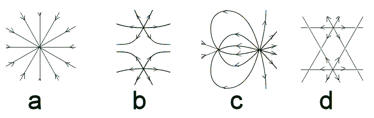
Discuss this with your fellow students in the
discussion forum!
Review the rules for drawing electric field lines.
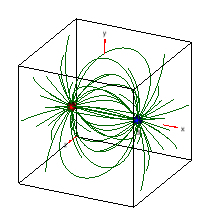
The electric field exists in 3-dimensional space. Below you can explore
3D drawings of the electric field lines of two charges.
Please click on the image!
You can change the
magnitude (arb. units), sign, and position (arb. units) of the each charge. You can use the mouse
to change your viewing angle and zoom in or out. To view field lines of
one charge only, choose zero for the magnitude of charge B.
Usually we try to visualize the magnitude and direction of the electric field
by drawing field lines in a plane in two dimensions. For two or three
charged spheres lying in a plane, we could draw the projections of the field
lines onto this plane. But that would make it impossible to represent the
exact direction of each line. We could also only draw field lines that lie
in that plane. Then the directions of the drawn lines would be correct,
but we would missing most of the lines, and the number of lines would not be proportional to the magnitude of the charge. So we make a hybrid 2D
drawing. For the directions, we only choose field lines lying in the
plane, but we scale the number of these lines up to the number we would get from
a projection. Therefore, for charged spheres lying in a plane, the field
strength in a 2D drawingsis not proportional to the density of the field lines,
but to the square of the density of the lines.
Simulation: Electric
Field Hockey
- This simulation looks down on an air hockey table. Instead of
hitting the puck, you move it using charges.
- Use the Practice mode for testing your ideas.
- Clear zeros everything, and Reset brings the puck back to the starting
point with the same charges.
- You can change the sign of the charge on the puck by checking or
un-checking the Puck is Positive option.
- You may want to investigate how to use multiple charges to make a goal.
The browser-compatible app uses
Java via Cheerpj
and takes long time to load, and it is slow,
but it usually works.
If you miss having regular lectures, consider this video lecture.
Lecture 2: Electric Field Lines
 A field
is a way of explaining action at a distance. Massive particles
attract each other. How do they do this, if they are not in contact with
each other? We say that massive particles produce gravitational fields.
A field is a condition in space that can be probed. Massive
particle are also the probes that detect a gravitational field. A
gravitational field exerts a force on massive particles. The magnitude of the
gravitational field produced by a massive object at a point
P is the gravitational force per unit mass it exerts on another massive
object located at that point. The direction of the gravitational field is
the direction of that force. We calculate the gravitation field
produced by a mass distribution using Newton's law of gravitation.
A field
is a way of explaining action at a distance. Massive particles
attract each other. How do they do this, if they are not in contact with
each other? We say that massive particles produce gravitational fields.
A field is a condition in space that can be probed. Massive
particle are also the probes that detect a gravitational field. A
gravitational field exerts a force on massive particles. The magnitude of the
gravitational field produced by a massive object at a point
P is the gravitational force per unit mass it exerts on another massive
object located at that point. The direction of the gravitational field is
the direction of that force. We calculate the gravitation field
produced by a mass distribution using Newton's law of gravitation. Consider a
point charge Q located at the origin.
Consider a
point charge Q located at the origin. If
Q is negative, then the electric field points radially towards the charge.
If
Q is negative, then the electric field points radially towards the charge. Examples:
Examples: The
field lines of two positive charges of equal magnitude separated by a
distance d.
The
field lines of two positive charges of equal magnitude separated by a
distance d. Every water molecule (H2O)
consists of one oxygen atom and
two hydrogen atoms. A water molecule has no net charge because the
number of positively charged protons equals the number of negatively
charged electrons in each atom. In the water molecule, each hydrogen
atom is bound to the oxygen atom by a covalent
bond. The hydrogen atom and the oxygen atom share an
electron, which has a slightly higher probability to be closer to the
oxygen atom than to the hydrogen atom. This results in a polar molecule, in which the
oxygen
"side" of the molecule has a slight negative charge, while the hydrogen
"sides" have a slight positive charge. Because water is a polar
molecule it dissolves many inorganic and organic materials. Organisms
can build macromolecules to attract or repel water as needed simply by
varying the charge on side chains.
Every water molecule (H2O)
consists of one oxygen atom and
two hydrogen atoms. A water molecule has no net charge because the
number of positively charged protons equals the number of negatively
charged electrons in each atom. In the water molecule, each hydrogen
atom is bound to the oxygen atom by a covalent
bond. The hydrogen atom and the oxygen atom share an
electron, which has a slightly higher probability to be closer to the
oxygen atom than to the hydrogen atom. This results in a polar molecule, in which the
oxygen
"side" of the molecule has a slight negative charge, while the hydrogen
"sides" have a slight positive charge. Because water is a polar
molecule it dissolves many inorganic and organic materials. Organisms
can build macromolecules to attract or repel water as needed simply by
varying the charge on side chains.
 Problem:
Problem:
 The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is
The most important application of the above result is
the superposition of the fields from two planar charge distributions which are
separated by some distance d. Place a uniformly charged plane with charge
density σ at x = +d/2 and a similar plane with charge density -σ at x = -d/2. The field due to the upper plane of charge is

