At the end of the 19th century more advanced measurement techniques allowed scientists to make previously impossible measurements.  Results of many new measurements involving light did not agree with predictions of the classical model.  Postulating the existence of photons lead to explanations for the many new experimental results.

Photons

Like all EM waves, light transports energy across space.  The intensity (energy per unit area and unit time) is proportional to the square of the amplitude of the electric field of the light wave.  This energy, however, arrives at a receiver not continuously but in discrete units called photons.  The energy transported by an electromagnetic wave is not continuously distributed over the wave front.  It is transported in discrete packages. Photons are the particles of light.

Properties of photons

• Photons always move with the speed of light.
• Photons are electrically neutral.
• Photons have no mass, but they have energy E = hf = hc/λ.  Here h = 6.626*10^-34 Js is a universal constant called Planck's constant.  The energy of each photon is inversely proportional to the wavelength of the associated EM wave.  The shorter the wavelength, the more energetic is the photon. The longer the wavelength, the less energetic is the photon.
  • A laser beam and a microwave beam can carry the same amount of energy.  In this case the laser beam contains a smaller number of photons, but each photon in the laser beam has a higher energy than the photons in the microwave beam.
• Photons can be created and destroyed.  When a source emits EM waves, photons are created.  When photons encounter matter, they may be absorbed and transfer their energy to the atoms and molecules.  Creation and destruction of photons must conserve energy and momentum.  The magnitude of the momentum of a photon is p = hf/c = h/λ.

Problem:

What is the energy of a photon of blue light (λ = 450 nm) and of a photon of red light (λ = 700 nm) in units of eV = 1.6*10^-19 J?

Solution:

• Reasoning:
  The photon that carry the energy of a electromagnetic wave with wavelength λ have energy E = hc/λ.
• Details of the calculation:
  E = hc/λ.
  Blue light: E = (6.626*10^-34 Js)(3*10⁸ m/s)/(450*10^-9 m) = 4.4*10^-19 J = 2.76 eV
  Red light: E = (6.626*10^-34 Js)(3*10⁸ m/s)/(700*10^-9 m) = 2.8*10^-19 J = 1.8 eV

Conversions

h = 6.626*10^-34 J s = 4.136*10^-15 eV s  
unit of energy: 1 eV = 1.6*10^-19 J 
useful product:  hc = 1240 eV nm

The unit of electronvolt (eV), is not an SI unit.  1 eV is the amount of kinetic energy gained or lost by a free electron or proton when accelerating through an electric potential difference of one volt in free space.  This is a small amount of energy, but energy changes in atomic scale physics are usually on the order of eV, so eV is a useful and convenient unit for atomic scale physics. 

Example:

• If you want to an electron with 100 eV kinetic energy, just accelerate it through a potential difference of 100 V.
• If you want to stop an electron with 100 eV kinetic energy, just decelerate it through a potential difference of 100 V.

The photoelectric effect

In 1905, Einstein used the discrete nature of light to explain the photoelectric effect (Nobel Prize in Physics in 1921).  To demonstrate this effect, light is shone on a metal surface.  If the frequency of the light is higher than the cutoff frequency f_c, then electrons are released.  No photoelectric electrons are emitted if the frequency of the light falls below this cutoff frequency f_c.  For many metal surfaces the frequency of blue light is greater than f_c and the frequency of red light is less than f_c.  If red light is shone on the surface, no electrons are emitted, no matter what the intensity of the light (within reasonable limits).  If blue light is shone on the surface, electrons are emitted.  The number of emitted electrons depends on the intensity of the light.  But even if the intensity is reduced to a very low value, electrons are still emitted, albeit at a very low rate.

The photoelectric effect cannot be understood within the wave picture of light. To eject an electron from a metal surface a certain amount of energy Φ must be supplied to this electron.  Φ is called the work function of the metal.   It only depends on the material.  (If no energy were required to free the electrons, they would just leave ordinary pieces of metal.)  In the wave picture the energy of the light beam does not depend on the frequency, but only on the intensity, which is proportional to the square of the amplitude.  Einstein explained the photoelectric effect by postulating that an electron can only receive the large amount of energy necessary to escape the metal from the EM wave by absorbing a single photon.  If this photon has enough energy, the electron is freed.  Excess energy appears as kinetic energy of the electron.  The maximum kinetic energy of the electron is given by

E_max = hf - Φ. 

If the photon does not have enough energy, then the electron cannot escape the metal.  The cutoff frequency is f_c = Φ/h, when E_max = 0.
 

Problem:

Molybdenum has a work function of 4.2 eV.  Find the cutoff frequency and cutoff wavelength for the photoelectric effect.

Solution:

• Reasoning:
  To eject an electron from a metal surface a certain amount of energy Φ must be supplied to this electron.  We need a minimum photon energy hf_c = Φ.
• Details of the calculation:
  hf_c = Φ,
  f_c = Φ/h = (4.2 eV)(1.6*10^-19 J/eV)/(6.626*10^-34 Js) = 1.01*10¹⁵ Hz is the cutoff frequency.
  λ_c = c/f_c = 296 nm is the cutoff wavelength.

Problem:

Electrons are ejected from a metal surface with speeds ranging up to 4.6*10⁵ m/s when light with a wavelength of 625 nm is used.
(a) What is the work function of the surface?
(b) What is the cutoff frequency of the surface?

Solution:

• Reasoning:
  To eject an electron from a metal surface a minimum amount of energy Φ must be supplied to this electron.
  If the photon ejecting the electron has more energy, then the excess energy is given as kinetic energy to the ejected electron.
  We have E_max = hf - Φ, where E_max is the maximum kinetic energy of the ejected electron.
• Details of the calculation:
  (a) Φ = hf - E_max.  E_max = ½mv² = ½(9.1*10^-31 kg)(4.6*10⁵ m/s)² = 9.63*10^-20 J.
  hf = hc/λ = (6.626*10^-34 Js)(3*10⁸ m/s)/(625*10^-9 m) = 3.18*10^-19 J.
  Φ = (3.18*10^-19 J) - (9.63*10^-20 J) = 2.21*10^-19 J is the work function of the surface.
  
  (b) f_c = Φ/h = (2.21*10^-19 J)/(6.626*10^-34 Js) = 3.35*10¹⁴ Hz is the cutoff frequency.

Problem:

Light of wavelength 500 nm is incident on sodium with a work function of 2.28 eV.  What is the maximum kinetic energy of the ejected photoelectron?

Solution:

• Reasoning:
  To eject an electron from a metal surface a minimum amount of energy Φ must be supplied to this electron.
  If the photon ejecting the electron has more energy, then the excess energy is given as kinetic energy to the ejected electron.
  We have E_max = hf - Φ, where E_max is the maximum kinetic energy of the ejected electron.
• Details of the calculation:
  E_max = hf - Φ = hc/λ - Φ.
  hf = hc/λ = (6.626*10^-34 Js)(3*10⁸ m/s)/(500*10^-9 m) = (3.98*10^-19 J)(1 eV)/(1.6*10^-19J) = 2.48 eV.
  E_max = 0.2 eV.

Photon momentum

Electromagnetic waves transport energy and momentum.  Therefore photons transport energy and momentum.  The magnitude of momentum of a photon with energy E = hf is p = E/c = hf/c = h/λ.  When an electromagnetic wave interacts with a small particle, it can exchange energy and momentum with the particle.  Momentum is a vector, momentum is conserved in interactions, and when two particles interact, the rate of change of one particle's momentum is equal to the force exerted on it by the other particle.  The force exerted on a particle by a photon is equal to the momentum transferred to it per unit time.  Optical tweezers use this force to provide a non-invasive technique for manipulating microscopic-sized particles with light.  They have become an important tool for the life sciences to answer questions and generate knowledge of biological significance.

Link:  Optical tweezers

The Compton effect

The Compton effect or Compton scattering (discovered in 1923, Nobel Prize in Physics in 1927) is another famous experiment supporting the existence of photons.  To observe the Compton effect, x-rays are scattered from (nearly) free electrons.  To understand Compton scattering we must think of photons as particles.

Imagine an incoming photon scattering off a stationary electron.

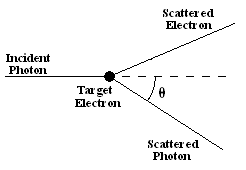
After the collision the photon's and the electron's trajectory will be at some angles with respect to the direction of the incoming photon.  If we know the energy and momentum of the incoming photon, and the angle the outgoing photon's trajectory makes with the direction of the incoming photon, then we can determine the outgoing photon's energy using energy and momentum conservation.  (This is the same way we treat billiard-ball collisions, except we use the relativistic formulas for energy and momentum, since the photon always moves with the speed of light.)

We find the following for the relationship between the initial and final momentum of the photon:

1/p_f - 1/p = (1 - cosθ)/(m_ec).

It is traditional to rewrite this expression in terms of the change of the photon's wavelength.

Δλ = (λ_f - λ_i) = [h/(m_ec)](1 - cosθ).

The quantity h/(m_ec) = 0.00243 nm = 2.43 pm is called the Compton wavelength for photon-electron collisions.
The Compton wavelength is the amount by which the photon's wavelength changes when it scatters through 90^o.  The change in wavelength is smaller if the scattering angle is less than 90^o, and is a maximum of twice the Compton wavelength if the photon scatters backwards through 180^o. 

Note:  The change of the photon's wavelength does not depend on the wavelength of the incident photon, only on the Compton wavelength and the scattering angle.

The Compton wavelength for photon-electron collisions is very small (~10^-12 m) and therefore the percentage change in the wavelength of the photon is very small, unless the incident photon has a very short wavelength.  The Compton effect is only observable with very short wavelength photons.  Only then does the change in the wavelength Δλ become an appreciable fraction of the wavelength λ.

Problem:

Photons of wavelength λ scatter elastically on free protons initially at rest.  By how much does the wavelength of the photons scattered at 90^o increase?

Solution:

• Reasoning:
  The amount by which the photon's wavelength changes when it scatters through 90^o off a particle is Δλ = [h/(m_particlec)]
• Details of the calculation:
  Δλ = (λ_f - λ_i) = [h/(m_pc)](1 - cosθ), where m_p is the mass of the proton.
  For θ = 90^o, Δλ = h/(m_pc) = 1.32 *10^-15 m = 1.31 fm.
  For photon-proton collisions the Compton wavelength is even smaller than for photon-electron collisions, and the Compton effect is harder to measure and verify experimentally.

Embedded Question 1

• A 100 W incandescent light bulb emits light uniformly in all directions.  About 10% of the bulb's energy output consists of visible light with an average wavelength of 580 nm,  You stand approximately 10 m from the bulb.  Estimate how many visible light photons from the bulb you will intercept. 

Discuss this with your fellow students in the discussion forum!  There is no exact answer.  What assumptions do you make to arrive at your estimate?