In one dimension, wave functions are often denoted by the symbol ψ(x,t).  They are functions of the coordinate x and the time t.  But ψ(x,t) is not a real, but a complex function, the Schroedinger equation does not have real, but complex solutions.

The wave function of a particle, at a particular time, contains all the information that anybody at that time can have about the particle.  But the wave function itself has no physical interpretation.  It is not measurable.  However, the square of the absolute value of the wave function has a physical interpretation.  In one dimension, we interpret |ψ(x,t)|² as a probability density, a probability per unit length of finding the particle at a time t at position x.

The probability of finding the particle at time t in an interval ∆x about the position x is proportional to |ψ(x,t)|²∆x.

This interpretation is possible because the square of the magnitude of a complex number is real.  For the probability interpretation to make sense, the wave function must satisfy certain conditions.  We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.  This leads to the requirements listed below.

• The wave function must be single valued and continuous. The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
• We must be able to normalize the wave function.  We must be able to choose an arbitrary multiplicative constant in such a way, so that if we sum up all possible values ∑|ψ(x_i,t)|²∆x_i  we must obtain 1.  The total probability of finding the particle anywhere must be one.  (The area under the curve |ψ(x,t)|² must be 1.)

Examples:

This is an acceptable wave function.  It is single valued and continuous.

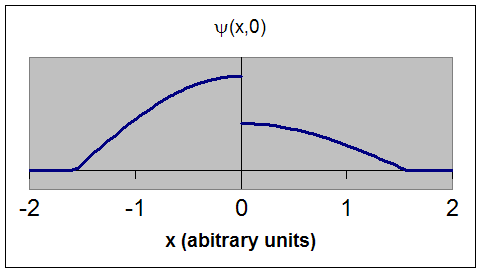
This is an unacceptable wave function.  ψ(x,0) does not have a unique
single value at x = 0.  The wave function is not continuous.

Problem:

Consider many particles, each at t = 0 described by a wave function ψ(x,0) = (2/π)^½cos(x) for x between -π/2 and +π/2 and ψ(x, 0) = 0 for all other x.  If the position of each particle is measured at t = 0, what is the average position of all the particles?

Solution:

• Reasoning:
  Each particle can be found in a small interval ∆x about any x between -π/2 and +π/2 with probability (2/π)cos²(x) ∆x.  Each particle is just as likely to be found at x > 0 than at x < 0.  The average position is x = 0.  The most likely position to find a particle is also x = 0, because that is where the square of the wave function has its maximum value.

Often we want to make predictions about the energy of a particle.  If we know the eigenfunctions of the energy operator, we know the associated eigenvalues, and therefore the possible outcomes of an energy measurement.  If a particle is confined in some potential well, then its energy eigenfunctions resemble standing waves in classical physics.  The energy eigenfundtion ψ(x,t) for a confined particle can be written as the product some real function ψ(x) of space and some complex function of time.  The complex function of time just describes the oscillations in time.
One of the simplest operations we can perform on a wave function is squaring it.  Squaring the wave function give us probability per unit length of finding the particle at a time t at position x.  For energy eigenfunctions this probability is independent of time, since the square of the complex function of time is the real number 1.  The probability of finding the particle in an interval ∆x about the position x is equal to ψ(x)²∆x.  Energy eigenstates are therefore called stationary states.  The probability is stationary, it does not change with time.

Energy and position are incompatible measurements.  Knowing the energy of a particle prevents us from knowing its position and tracking it.  A stationary-state wave function contains no information about the position of the particles as a function of time.  All we get is probabilities.  We can certainly make a measurement and determine the position of a particle at a particular time, but then we loose the information about its energy.

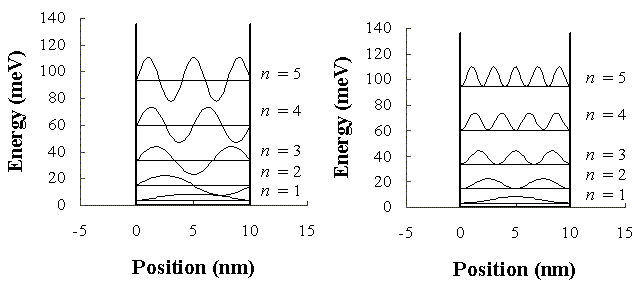
Example 1:

An electron (m = 9.109*10^-31 kg) is confined in a one-dimensional square well with infinitely high walls and width L = 10 nm.  The figure on the right shows

• (a)  the lowest five energy levels E_n = n²π²ħ²/(2mL²), and the corresponding energy eigenfunctions ψ_n(x) = (2/L)^½sin(nπx/L).  These wave functions look like standing waves on a string. 
• (b)  the corresponding probability density functions
  ψ_n(x)² = (2/L)sin²(nπx/L).

In the figure the wave functions and the probability density functions have an arbitrary magnitude and are shifted by the corresponding electron energy.

Note:  The electron is not "smeared out" in the well.  We just do not have exact position information, because energy and position are incompatible observables.

The lowest possible energy of the confined particle is its ground-state energy.  All other possible energies are excited-state energies.  A particle can make transitions between different energy levels when it is interacting with its environment.  If a particle makes a transition from a lower energy level to a higher energy level, it has to absorb an amount of energy ∆E = E_high - E_low from the outside world.  It can absorb a photon with energy hf = ∆E, or it can receive the required energy from another particle in a collision.  If the particle makes a transition from a higher energy level to a lower energy level, it has to release an amount of energy ∆E = E_high - E_low to the outside world.  One way to do this is to emit a photon of energy hf = ∆E.

Because the energy levels are quantized, the energies of photons involved in transitions are quantized. The particle in the well can only interact with photons of certain energies, it can only emit or absorb light of certain colors.

Confinement always leads to energy quantization.

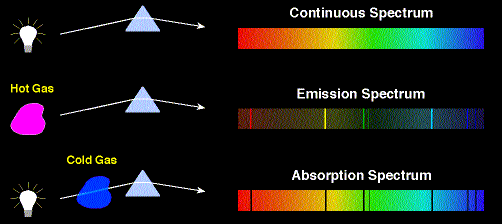
Electrons in atoms are not confined in a square well, but they are confined.  This confinement leads to energy quantization.  If we measure the energy of an electron in an atom, we can only measure a of a set of discrete values.  The energies of the electrons in atoms are quantized.  Atomic spectra reveal this quantization.  Light from a hot filament contains all the colors of the rainbow.  But light given off or absorbed by individual atoms consists of a unique set of colors.

Example 2:

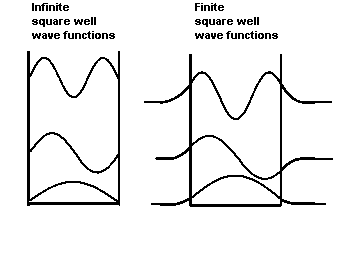The figures on the right show the shapes of the ground-state and excited-state wave functions of a particle trapped in a square well with infinitely high wall and one with walls of finite height.
The wave functions in the finite well have exponentially decaying tails inside the walls, in the "classically forbidden region".  A particle has negative kinetic energy in this region, which classically is impossible.

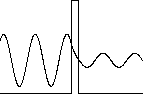In quantum mechanics the solutions in the classically forbidden regions are exponentially decaying solutions, and they fall to zero rapidly.  But if the region in which the kinetic energy is negative is narrow, then it is possible for the exponential solution to smoothly connect two oscillating solutions with positive kinetic energy on both sides of the region, and for the particle to have a finite probability of presence in that region. This leads to the phenomena of barrier penetration and tunneling.

The tunneling probability strongly depends on the barrier's width and height.  Most particles approaching the barrier are reflected, but a few tunnel through the barrier.  The probability P of finding the particle with energy E on the other side of the energy barrier of height U > E decreases exponentially as P = exp(-2αd), where d is the width of the barrier and α = [(2m/ħ² )(U - E)]^½.  The tunneling probability is smaller for more massive particles, for wider barriers, and for higher barriers (as compared to the energy of the particle).

Problem:

A beam of electrons with kinetic energy E is incident on a potential barrier.  The height of a potential barrier is 6 eV and the the width is 0.7 nm.  What is the energy E of each electron if the tunneling probability or transmittance is 0.001, i.e. if 0.1% of the electrons in the beam tunnel through the barrier?

Solution:

• Reasoning:
  The tunneling probability can be expressed as
  P = exp(-2αd), where α = [(2m/ħ² )(U - E)]^½,  Here d = 7*10^-10 m.
• Details of the calculation:
  The mass of the electron is 9.1*10^-31 kg and U = 6 eV*1.6*10^-19 J/eV = 9.6*10^-19 J.
  ln(P) = -2αd, so α = -ln(0.001)/(2*7*10^-10 m) = 4.93*10⁹/m.
  E = U - ħ²α²/(2m) = 9.6*10^-19 J - (1.054*10^-34 Js *4.93*10⁹/m)²/(2*9.1*10^-31 kg) = 8.11 x 10^-19 J = 5.07 eV.
  An electron with E = 5.07 eV has a probability of 0.001 or 0.1% of tunneling through the 6 eV barrier.

Application: Tunneling Microscopy

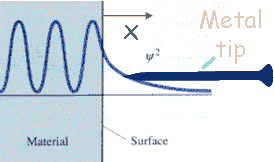One can exploit tunneling to measure the electron density on a material's surface.

The electron probability density associated with metal atoms at a surface extends a very small distance above the surface.  When a very sharp tip is brought sufficiently close to such a surface, there is a strong interaction between the electrons on the surface and that of the tip, and an electric tunneling current flows when a small voltage is applied.  At a separation of a few atomic diameters, the tunneling current rapidly increases as the distance between the tip and the surface decreases.  This rapid change of tunneling current with distance results in atomic resolution, if the tip is scanned over the surface to produce an image.

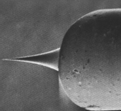
Image of an actual tip.

The tip is mounted on a piezoelectric tube, which allows tiny movements by applying a voltage at its electrodes.  Thereby, the electronics of the STM system control the tip position in such a way that the tunneling current and, hence, the tip-surface distance is kept constant, while at the same time scanning a small area of the sample surface.  This movement is recorded and can be displayed as an image of the surface topography.  Under ideal circumstances, the individual atoms of a surface can be resolved and displayed.
This explanation is illustrated by an animated sequence.

Some STM images are shown below.

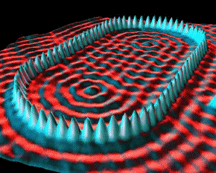
Iron atoms on a copper surface

The DNA double helix

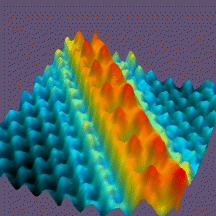
Cs atoms (red) on the GaAs (blue)

What if Quantum Mechanics determined the behavior of macroscopic objects?

You expect a car parked in your garage to stay parked until someone moves it.  What if Planck's constant were large, and Quantum Mechanics determined the behavior of your car?

First consider the uncertainty principle.  If you want to make sure your car only bounces gently around in the garage, you must build a big garage.  Now consider barrier penetration.  Nobody has touched your car.  Is it still parked in your garage?

If Quantum Mechanics governed the behavior of your car, you could never be completely sure.  Even though nobody touched it, nobody opened the door, and nobody broke down the wall, the car may be gone.  It may have just moved through the wall.  The thicker the wall, the less likely is this tunneling.