So light is a stream of photons! But why then does it act like a wave? Why do we
observe diffraction and interference?
 Photons definitely do not behave like macroscopic
particles, even very small macroscopic particles.
Photons definitely do not behave like macroscopic
particles, even very small macroscopic particles.
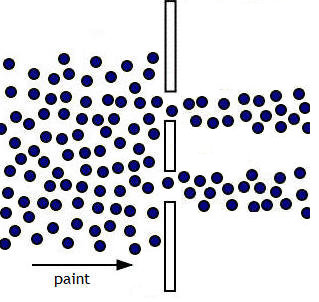
Consider very small macroscopic particles, such as paint droplets from a paint
gun. If we positioned a
mask with two slits in front of a wall and used a paint gun to spray
paint through the slits onto the wall, the paint does not produce an interference pattern on the wall.
If the slits are sufficiently spaced apart, we observe
two sharp lines of paint on the wall, images of the two slits through
which the paint was sprayed. If the spray is very weak and we may see
droplet arrive individually, but the droplets will eventually overlap and merge
into the two lines. If the slits are very closely spaced the two lines may
merge into just one line.
Even if we make the slits as narrow as
possible and put them as close together as possible for the paint droplets to
still pass through them without clogging them up, we will only see one line.
We will not observe an interference pattern.
The figure on the right shows the pattern we
expect to observe when paint is sprayed through two slits sufficiently spaced
apart.
When we send a beam of photons through a single slit, we observe a single-slit
diffraction pattern on a screen. If we lower the intensity of the beam and
use a detector that can detect single photos, we can observe single photons
arriving one at a time at seemingly random locations, but over time they will
build up a single-slit diffraction pattern.
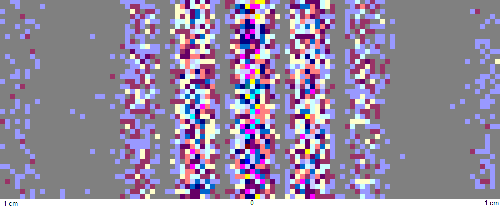 When we send a beam of photons through
two closely spaced slits, we observe an double-slit interference pattern in the
regions where there are no single slit diffraction minima. If we lower the
intensity of the beam and use a detector that can detect single photos, we can
observe single photons arriving one at a time at seemingly random locations, but
over time they will build up a double-slit interference pattern.
When we send a beam of photons through
two closely spaced slits, we observe an double-slit interference pattern in the
regions where there are no single slit diffraction minima. If we lower the
intensity of the beam and use a detector that can detect single photos, we can
observe single photons arriving one at a time at seemingly random locations, but
over time they will build up a double-slit interference pattern.
If we device an experiment that allows us to determine which slit the photon went through, the interference pattern vanishes
and just the diffraction pattern remains.
Simulate the experiment
(Excel, download and allow macro to run.)
The linked Excel spreadsheet lets you simulate a double slit experiments
using a detector that can detect individual photons. The two slits
are 50 micrometer wide and 150 micrometer apart. The distance from
the slits to the screen is 1 m. The pattern is a product of a
single slit and a double slit diffraction pattern. Individual
photons arrive at the screen. After many photons have arrived, the
interference pattern emerges. You can vary the wavelength and
intensity of the incident light.
(Observe that some interference maxima are missing because they fall
onto diffraction minima.)
How is it possible for light to propagate as if it were a wave and
yet to be detected as if it were a particle? How can a single
particle interfere with itself? This paradox is the central theme
in Richard Feynman's introduction to the fundamentals of quantum
mechanics:
"We choose to examine a phenomenon which is impossible, absolutely
impossible, to explain in any classical way, and which has in it the
heart of quantum mechanics. In reality, it contains the
only mystery. We cannot make the
mystery go away by explaining how it works . . . In telling you how it
works we will have told you about the basic peculiarities of all quantum
mechanics."
So what is light, an electromagnetic wave or a stream of photons? What is our current understanding of the
nature of light?
Photons are quanta or packets of energy.
But these quanta behave nothing like macroscopic particles.
- For a macroscopic particle we assume that we can measure its position
and its velocity at any time with arbitrary precision and accuracy.
Given that we have done this, we can predict with arbitrary precision and
accuracy its subsequent motion.
- For a photon we cannot make make such precise and accurate predictions.
In a single or double slit experiment, we can only predict the probability that the photon will strike the screen in a given spot.
That probability can be calculated using the wave equation for
electromagnetic waves.
Where that equation predicts a high light intensity, the
probability is large, and where it predicts a low light intensity, the
probability is small.
In other words, where the wave equation predicts constructive interference,
the photon is likely to be detected, and where it predicts destructive
interference, the probability of detecting the photon is small or zero
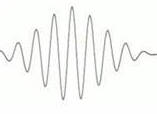 To track individual photons or groups of photons,
the EM wave we use to predict their behavior must be a wave pulse or wave packet. A wave packet has finite
extend, and the photons will be found in regions where the wave packet
has non-zero amplitude. But only waves that extend forever
in space and time have a precisely defined wavelength or frequency.
The wavelength and frequency of wave packets that are supposed to
describe a fairly well localized wave pulse cannot be precisely known,
but only within some uncertainty.
To track individual photons or groups of photons,
the EM wave we use to predict their behavior must be a wave pulse or wave packet. A wave packet has finite
extend, and the photons will be found in regions where the wave packet
has non-zero amplitude. But only waves that extend forever
in space and time have a precisely defined wavelength or frequency.
The wavelength and frequency of wave packets that are supposed to
describe a fairly well localized wave pulse cannot be precisely known,
but only within some uncertainty.
In Physics 221 you analyzed
sound
waves. Using Fourier analysis you found that wave packets of sound
contain many different wavelengths or frequencies.
Fourier analysis shows that for all wave packet the product of the
uncertainties (spread) in their wave number k = 2π/λ and in their length in
space x must be on the order of or larger than 1.
We write Δx Δk ~ 1.
Similarly Fourier analysis shows that for all wave packets the product
of the uncertainties (spread) in their angular frequency ω = 2πf and
in their length in time t must be on the order of or larger than 1.
We write Δt Δω ~ 1.
Since for photons the energy is E = hf and momentum is p = h/λ, we cannot precisely know the energy and
momentum of the individual photons in a wave packet. Rewriting k = 2π/λ
= (2π/h)p, we find
Δx Δp ~ h/2π.
This is the famous Heisenberg uncertainty principle. Here we are applying it to a photon. For a
photon, we cannot predict its position and momentum with absolute certainty.
The product of the uncertainties is on the order of h/2π or greater. The quantity h/2π is often denoted
by ћ (hbar), ћ = 1.054*10-34 Js.
Rewriting ω = 2πf = (2π/h)E, we find
Δt ΔE ~ h/2π.
This is another form of the uncertainty principle. If there is a limit
to the observation time, there will be an
uncertainty in the energy.
Problem:
A pulsed laser produces femtosecond (10-15 s) pulses of near
infrared light with 780 nm nominal wavelength. What is the minimum range
of energies of the photons in the pulses.
Solution:
- Reasoning:
We can only observe a pulse for 10-15 s. If there is
is a limit to the observation time, there will be an uncertainty in the
energy.
- Details of the calculation:
Δt ΔE ~ ћ. ΔE = ћ/(10-15 s) =
1.05*10-19 J = 0.65 eV.
The nominal photon energy = hf = hc/λ = (1240 eV nm)/(780 nm) = 1.59 eV.
The uncertainty in the photon energy ΔE/E = (0.65 eV)/(1.59 eV) = 41%.
We have the same percentage uncertainty in the photon frequency and
wavelength.
Very short laser pulse do not have a well-defined wavelength.
 Photons definitely do not behave like macroscopic
particles, even very small macroscopic particles.
Photons definitely do not behave like macroscopic
particles, even very small macroscopic particles.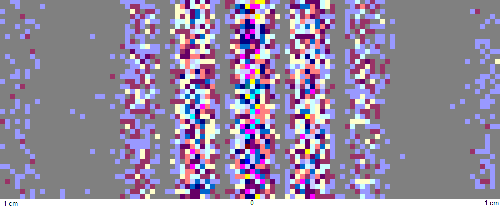 When we send a beam of photons through
two closely spaced slits, we observe an double-slit interference pattern in the
regions where there are no single slit diffraction minima. If we lower the
intensity of the beam and use a detector that can detect single photos, we can
observe single photons arriving one at a time at seemingly random locations, but
over time they will build up a double-slit interference pattern.
When we send a beam of photons through
two closely spaced slits, we observe an double-slit interference pattern in the
regions where there are no single slit diffraction minima. If we lower the
intensity of the beam and use a detector that can detect single photos, we can
observe single photons arriving one at a time at seemingly random locations, but
over time they will build up a double-slit interference pattern.  To track individual photons or groups of photons,
the EM wave we use to predict their behavior must be a wave pulse or wave packet. A wave packet has finite
extend, and the photons will be found in regions where the wave packet
has non-zero amplitude. But only waves that extend forever
in space and time have a precisely defined wavelength or frequency.
The wavelength and frequency of wave packets that are supposed to
describe a fairly well localized wave pulse cannot be precisely known,
but only within some uncertainty.
To track individual photons or groups of photons,
the EM wave we use to predict their behavior must be a wave pulse or wave packet. A wave packet has finite
extend, and the photons will be found in regions where the wave packet
has non-zero amplitude. But only waves that extend forever
in space and time have a precisely defined wavelength or frequency.
The wavelength and frequency of wave packets that are supposed to
describe a fairly well localized wave pulse cannot be precisely known,
but only within some uncertainty.