Quick Review

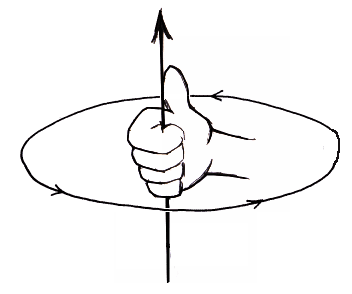In three dimensions, a particle can have angular momentum.  Angular momentum is most often associated with rotational motion and orbits.  For a classical particle orbiting a center, we define the orbital angular momentum L of a particle about an axis as L = mr²ω, where r is the perpendicular distance of the particle from the axis of rotation and ω is its angular speed, in radians/s.  Angular momentum is a vector.  The magnitude of the orbital angular momentum of the particle is L = mrv_perp = mr²ω.  Here v_perp is the component of the particles velocity perpendicular to the axis of rotation.   The direction of the angular momentum is given by the right-hand rule.  The angular momentum of isolated systems is conserved.  If no external torque acts on a system of interacting objects, then their total angular momentum of the system is constant.  The angular momentum of a classical particle can have any magnitude and point in any direction.

Please click here for a 3D review of the right-hand rule!

Quantum mechanics predicts that all angular momentum is quantized in magnitude as well as in direction.

If we measure the magnitude of the angular momentum, we will only measure discrete values, and if we choose a coordinate system and measure its projection along one of the coordinate axis, we will only measure discrete values.

Orbital angular momentum is quantized.

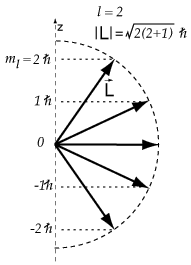The possible values that we can measure for the square of the magnitude of the orbital angular momentum are L² = l(l + 1)ħ².  It is customary to give L², and not L = l(l + 1))^½ħ.  The quantum number l is the label we use to identify the different values we can measure; l is a non-negative integer, l = 0, 1, 2, ... .

The projections of the angular momentum along any axis are also quantized.  We can know the magnitude and the projection along any one axis at the same time.  These measurements are compatible.
The possible projections or components along any axis, for example the z-axis, are quantized, we have L_z = mħ.  The quantum number m is an integer, and m can take on values from -l to l in integer steps.  Given l, there are 2l + 1 possible values for m.

The orbital angular momentum vector L is never precisely aligned with any coordinate axis.

Example:

Assume we have measured the magnitude of the orbital angular momentum and found L = (l(l + 1))^½ħ with l = 2.  Then the magnitude of the angular momentum vector is L = 6^½ħ = 2.45ħ.
It's possible projections along the z-axis are mħ =  -2ħ, -1ħ, 0, 1ħ, 2ħ.   The largest projection is 2ħ, which is smaller than 2.45ħ, the value we would get if the vector could point in the z-direction.

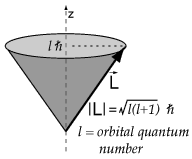If we measure L_z = 2ħ, then we know that L lies on a cone, as shown on the right, but we do not know its projections along the x and y axes. The orbital angular momentum vector L is never precisely aligned with a coordinate axis.

The components of the orbital angular momentum along different axes are incompatible observables.  L_x, L_y, and L_z cannot be known simultaneously.  If we measure the component of the angular momentum along one axis, we lose information about the components along the other axes.  We do, however, not lose information about the magnitude of the angular momentum.

Problem:

We have measured the square of the orbital angular momentum of a particle and have found the value L² = 30ħ².  If we now measured the z-component of the orbital angular momentum L_z, what are the possible outcomes of the measurement?

Solution:

• Reasoning:
  The measurements are compatible. 
• Details of the calculation:
  L² = l(l + 1)ħ², so l = 5.
  The possible outcome of a measurement of L_z are L_z = mħ, with m taking on values from -l to +l in integer steps.
  The possible outcomes therefore are mħ = -5ħ, -4ħ, -3ħ, -2ħ, -1ħ, 0, 1ħ, 2ħ, 3ħ, 4ħ, 5ħ.

Problem:

We have measured the square of the orbital angular momentum of a particle and have found the value L² = 30ħ².  We measured the z-component of the orbital angular momentum and found L_z = 0.  If we now measured the x-component of the orbital angular momentum L_x, what are the possible outcomes of the measurement?

Solution:

• Reasoning:
  The measurements L² and L_x are compatible, and l = 5 (see previous problem).
• Details of the calculation:
  The possible outcome of a measurement of L_x are L_x = mħ, with m taking on values from -l to +l in integer steps.
  The possible outcomes therefore are mħ = -5ħ, -4ħ, -3ħ, -2ħ, -1ħ, 0, 1ħ, 2ħ, 3ħ, 4ħ, 5ħ.
  But the measurements of L_x and L_z are incompatible.  After measuring L_x, we have lost the information about L_z.

Problem:

Assume the orbital angular momentum quantum number l of a particle is l = 2.
(a)  How many angles can the angular momentum L make with the z-axis?
(b)  Calculate the value of the smallest angle.

Solution:

• Reasoning:
  There are 2l + 1 possible values of m, or 2l +1 possible projections of L onto the z-axis.
• Details of the calculation:
  (a)  L can make 5 different angles with the z-axis.
  (b)  The largest positive projection yields the smallest angle.  We have cosθ = L_z/L = (mħ)/((l(l+1))^½ħ).
  The largest possible m is m = 2, so the smallest angle satisfies cosθ = 2/(√6) = 0.8165, θ = 35^o.