The periodic table

To study multi-electron atoms, imagine that we start with hydrogen and add electrons, one at a time.  At the same time we increase the number of protons and neutrons in the nucleus to keep the atom electrically neutral and the nucleus stable.  We will assume that as we add each electron, it falls down to the lowest energy state available.  If we start with a nucleus with one proton, and drop in one electron, the electron eventually falls down to the n = 1 state.  Its energy is E1 = -13.6 eV.  As we add a proton (and two neutrons) to form a helium nucleus and drop in another electron, we can expect the electron to also fall down to the n = 1 state.  The extra Coulomb attractive force of the two protons in the nucleus strengthens the binding of the electrons, but the repulsive force between the two electrons weakens it.  Experimentally, it takes 24.6 eV to remove an electron from helium, while only 13.6 eV are needed for hydrogen.  Thus the electrons are more tightly bound in helium, and we see that in helium the extra Coulomb attraction to the nucleus is more important than the repulsion between electrons.

Using helium as a guide, we should expect that when we go to lithium with 3 protons in the nucleus, the increased Coulomb attraction to the nucleus should cause lithium's three electrons to be even more tightly bound than helium's two.  This would lead us to predict that it takes even more than 24.6 eV to pull one of the electrons out of lithium.

This is not a good prediction.  Experimentally, the amounts of energy needed to remove electrons from lithium one at a time are 5.39 eV, 75.26 eV and 121.8 eV.  While two of lithium's electrons are tightly bound, one is very loosely bound, requiring less than half the energy to remove than it takes to remove the electron from hydrogen.  A possible explanation for the loose binding of lithium's third electron is that, for some reason, the electron does not fall down to the lowest energy n = 1 state.  It appears to be hung up in one of the higher energy, less tightly bound n = 2 states.  For n = 2, there are 4 different sets of quantum numbers (l, m) and 4 different wave functions.

Pauli Exclusion Principle

But why would the third lithium electron not fall down to the low energy n = 1 state?  In 1925, two separate ideas provided the explanation.  Wolfgang Pauli proposed that no two electrons were allowed to be in exactly the same state.  This is known as the Pauli exclusion principle.  But the exclusion principle seems to go too far, because in helium, both electrons are in the same n = 1, l = 0, m = 0 state.  If you cannot have two electrons in exactly the same state in an atom, then something must be different about the two electrons in helium.

Electron Spin

To explain this difference between the two electrons, two graduate students, Samuel Goudsmit and George Uhlenbeck, proposed that the electron had its own internal angular momentum.  This became known as spin angular momentum.  The special feature of the electron's spin is that it has two allowed projections along any axis, which we call spin up and spin down.  In helium you could have two electrons in the same n = 1 state if they had different spin projections, because then they would not be in identical states.  A state would be characterized by 4 quantum numbers, n, l, m, and ms, where ms tells us about the projection of the electron's spin on the z-axis.  Because the electron spin has only two allowed projections along any axis, we cannot add a third electron to the n = 1 state.  Lithium's third electron must stop at one of the higher energy n = 2 states.  Its energy is much less negative and therefore this electron is much less tightly bound than the first two electrons that went down to the n = 1 state.

The spin of a particle is closely related to its properties in statistical mechanics.  Particles with half-integer spin obey "Fermi-Dirac statistics" and are known as fermions.  They are subject to the Pauli exclusion principle, which forbids them from sharing a quantum states.  Particles with integer spin, on the other hand, obey "Bose-Einstein statistics" and are known as bosons.  These particles can share quantum states.

The periodic table

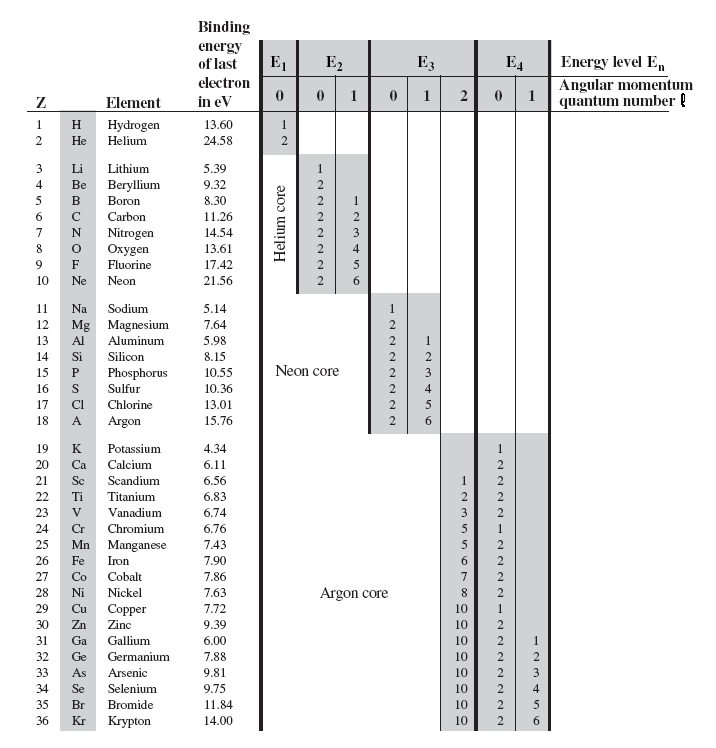imageAs we go to larger atoms, adding electrons one at a time, the n = 2 states begin to fill up.  Since there are four different values for (l, m), each with two allowed spin states, up to 8 electrons can fill the n = 2 states.  All the states with quantum number n = 2 are said to be in the n = 2 shell.  A shell refers to all the states with the same quantum number n.  A subshell refers to all the state with the same quantum numbers n and l.  When the n = 2 states are all filled we get to the element neon with two n = 1 electrons and eight n = 2 electrons.  Neon is an inert noble gas that is chemically similar to helium.  Adding one more electron by going to sodium, the eleventh electron has to go up into the n = 3 energy level since both the n = 1 and n = 2 states are full. This eleventh electron in sodium is loosely bound like the third electron in lithium, with the result that both lithium and sodium have similar chemical properties.  They are both strongly reactive metals.  The table on the right shows the electron structure and the binding energy of the last (most loosely bound) electron for the first 36 elements in the periodic table.

The general features of this table are that the lowest energy levels fill up first, and there is a large drop in binding energy when we start filling a new energy level.  We see these drops when we go from the inert gases helium, neon, and argon to the reactive metals lithium, sodium and potassium.  We can see that this sudden change in binding energy leads to a significant change in the chemical properties of the atom.  A closer look at the table shows that there is a relatively steady uniform increase in the electron binding as the energy level fills up.  The binding energy goes from 5.39 eV for lithium in fairly equal steps up to 21.56 eV for neon as the n = 2 energy level fills.  The pattern is more or less repeated as we go from 5.14 eV for sodium up to 15.76 eV for argon while filling the n = 3 energy level.  It repeats again in going from 4.34 eV for potassium up to the 14.00 eV for krypton.

A closer look also uncovers some exceptions to the rule that the lower n-states fill first.  The most notable exception is at potassium, where the n = 4 state with l = 0 begin to fill before the n = 3 states with l = 2.  To understand why the binding energy gradually increases as a shell fills up, and why the n = 3 , l = 2 states fill up late, we have to take a closer look at the electron wave functions and see how their shape affects the binding energy.

imageElectrons with no orbital angular momentum and therefore quantum number l = 0, have a finite probability of being very close to and even inside the nucleus.  They therefore sometimes feel a very strong, attractive force and are bound stronger to the atom.

imageElectrons with non-zero orbital angular momentum and therefore non-zero quantum number l, are never found inside the nucleus.  The larger l, the farther away they have to stay from the nucleus.  Since their potential energy U(r) is proportional to -1/r, they never see the most negative regions of the potential well and therefore are not as strongly bound to the atom.

As n increases, the difference between energy levels with quantum number n and n + 1 becomes smaller, and, starting with n = 3, electrons are more strongly bound in the n + 1, l = 0 energy level than in the n, l = 2 energy level.  For example, electrons fill the n = 4, l = 0 subshell before they fill the n = 3, l = 2 subshell.  Once the n = 4, l = 0 subshell has been filled, electrons can no longer have zero angular momentum, and they resume filling the n = 3, l = 2 subshell.

Notation

imageAn electron configuration is an enumeration of the values of n and l for all electrons of an atom.  The standard notation to describe atomic electron configurations is to denote each subshell by a number equal to its the principal quantum number n, a letter referring to its angular momentum quantum number l and a superscript giving the number of electrons in the subshell.  The electron subshells of atoms in their ground state are filled one electron at a time by putting each electron into the state with the lowest available energy.  The energy ordering of the subshells can be remembered from the diagram on the right.

Examples:

Element # of Electrons in Element Electron Configuration

He

2

1s2

Li

3

1s22s1

Be

4

1s22s2

O

8

1s22s22p4

Cl

17

1s22s22p63s23p5

K

19

1s22s22p63s23p64s1

Electrons in a subshell with l = 0 have wave functions and probability densities that are spherically symmetric.  The probability density of an electron in a subshell with l > 0 varies with angle.  However, when a subshell is completely filled, then the probability of finding an electron a given distance from the nucleus is the same for any angle. The superposition of all the possible angular probability distributions becomes again spherically symmetric.
Electrons are point particles. We either find an electron at a given position, or we do not find it.  If we find an electron, it has charge -qe.  Only if we average the amount of charge found in a given volume ∆V over time can we define a charge density or charge distribution ∆Q/∆V.  This average charge density is proportional to the probability density.  For a closed subshell the electron charge distribution is spherically symmetric.

Problem:

How many subshells and electron states are in the n = 5 shell?

Solution:

Problem:

(a) If one subshell of an atom has 9 electrons in it, what is the minimum value of l?
(b) What is the spectroscopic notation for this atom, if this subshell is part of the n = 3 shell and the atom is in its ground state.

Solution:

Problem:

In an atom, how many electron states are in the n = 3 shell?

Solution: