In addition to orbital angular momentum, many elementary particles have spin.  Spin is intrinsic angular momentum associated with elementary particles.  It is a purely quantum-mechanical phenomenon without any analog in classical physics.  Spin is not associated with any rotating internal parts of elementary particles; it is intrinsic to the particle itself.  An electron has spin, even though it is believed to be a point particle, possessing no internal structure.  Even a photon has spin.

Like all angular momentum, spin is quantized, and can only take on discrete values.  The square of the magnitude of the electron's spin is S² = s(s + 1)ħ² = 3/4ħ².  The spin quantum number s for the electron is equal to ½.  The spin angular momentum of an electron, measured along any particular direction, can only take on the values ħ/2 or -ħ/2.  We have S_z = m_sħ, with the quantum number m_s taking on values from -s to + s in integer steps, namely -½ and +½.  Electrons, protons, and neutrons are all "spin ½ particles".

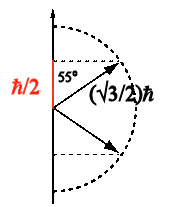
We can measure the orientation of the electron spin with respect to any axis (spin polarization).  These measurements yield two possible values, ~55^o aligned or anti-aligned.  Measurements of the orientation with respect to the x-, y-, and z-axis are incompatible.

Unlike orbital angular momentum, spin angular momentum is characterized by a quantum number s that can be an integer or a half integer, s = 0, ½, 1, 3/2, ... .  The quantum number m_s specifying the alignment can take on values from -s to + s in integer steps.  There are elementary particles with integer and with half-integer spin.  The photon, for example, is a spin 1 particle, s = 1 for the photon.  The photon's spin is responsible for the light's macroscopic property of polarization.  To find the net spin of a composite particle (such as a nucleus or an atom), we have to add the spin vectors of its constituents.  Composite particles can be integer or half-integer spin particles.