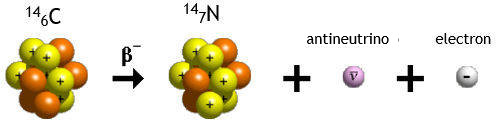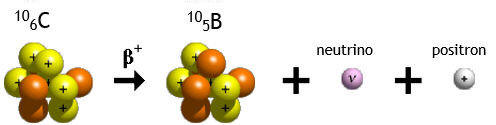Radioactive decay is the set of various processes by which an unstable atomic nucleus spontaneously emits subatomic particles. Decay is said to occur in the parent nucleus and produce a daughter nucleus. The SI unit for measuring radioactive decay is the becquerel (Bq). If a quantity of radioactive material produces one decay event per second, it has an activity of one Bq. Since any reasonably-sized sample of radioactive material contains very many atoms, a becquerel is a tiny level of activity.
The most common decay modes are alpha, beta, and gamma
decay. The subatomic particle emitted in alpha decay is a
positively charges alpha particle or He nucleus, the subatomic particle
emitted in beta decay is a negatively charged electron, and the
subatomic particle emitted in gamma decay is neutral photon or gamma
ray.
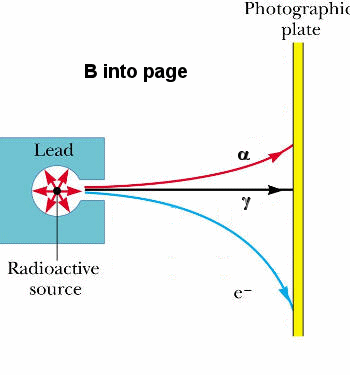
We can experimentally identify these particles by passing them through a region containing a magnetic field as shown on the right.
The neutrons and protons in a nucleus have various interactions. The
strong nuclear force, not observed at the familiar macroscopic scale, is the
most powerful force over subatomic distances. The electrostatic force is
significant. Also of importance is the weak force. The interplay of
these forces is very complex. If the configuration of the particles in a
nucleus shifts ever so slightly, the particles can possibly fall into a
lower-energy arrangement. The nucleus can spontaneously decay. The
resulting transformation changes the structure of the nucleus, it is a nuclear
reaction, in contrast to chemical reactions, which concern interactions of
electrons with nuclei.
Some nuclear reactions do involve external sources of energy, in the form of
"collisions" with outside particles. However, these are not considered
decay.
The decay of an unstable nucleus (radionuclide) is a quantum process. The probability that a given nucleus will decay in the next time interval Δt is independent of the history of the nucleus. The decay process is entirely random, and it is impossible to predict when a particular nucleus will decay. (If a particular nucleus has a 20% chance to decay in the next day, and it survives for one week, then after that week it still has a 20% chance of decaying in the next day.) Therefore, given a sample of a particular radioisotope, the number of decay events expected to occur in a small interval of time Δt is proportional to the number N of atoms present. The decay rate, ΔN/Δt, is proportional to N. The proportional constant λ is called the decay constant. We write
ΔN/Δt = -λN,
where the minus sign indicates that we are loosing nuclei from the initial species.
Different radionuclides decay at different rates, each
having its own decay constant λ. The solution to the above
differential equation gives the number of nuclei N(t) left after some
time interval t.
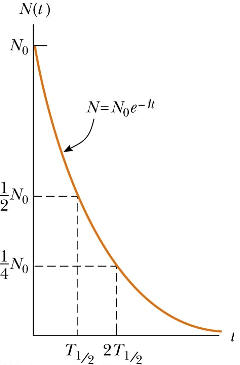
N(t) = N0exp(-λt).
This function represents exponential decay. It is
an approximate solution, for two reasons. Firstly, the exponential
function is continuous, but the physical quantity N can only take
positive integer values. Secondly, because it describes a random
process, it is only statistically true. However, in most cases, N
is a very large number and the function is a good approximation.
In addition to the decay constant λ, radioactive decay
is sometimes characterized by the mean lifetime.
Each atom "lives" for a finite amount of time before it decays, and the
mean lifetime is the arithmetic mean of all the atoms' lifetimes. It is
represented by the symbol τ, and is related to the decay constant by
τ = 1/λ.
Another commonly used parameter is the
half-life t½. Given
a sample of a particular radionuclide, the half-life is the time it
takes for half the radionuclides to decay.
When N(t)/N0 = exp(-λt) = ½, then λt = ln2, t = ln2/λ.
In terms of τ the half-life is given by
t½ = τ ln2 = ln2/λ.
Highly radioactive substances are quickly lost, while those that
radiate weakly endure longer. Half-lives of known radionuclides vary
widely, from 109 years for nearly stable nuclides, to 10-6
seconds for highly unstable nuclides.
We are often more interested in the decay rate R = -ΔN/Δt than in the number
N itself.
R(t) = λN = λN0exp(-λt) = R0exp(-λt),
with R0 = λN0. The decay rate decreases exponentially with time at the same rate as the number of nuclei.
A 2.71 g sample of KCl is found to be radioactive. It is decaying at a rate of 4490 Bq. The decay is traced to an isotope of potassium, 40K, which constitutes 1.17% of normal potassium. Calculate the half life of this nuclide.
Solution:
Alpha decay is a form of radioactive decay in which an atomic nucleus characterized by mass number A and atomic number Z ejects an alpha particle (a 4He nucleus) and transforms into a nucleus with mass number A - 4 and atomic number Z - 2 .
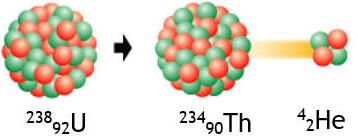
Thus the most common form of Uranium, 238U (A = 238, Z = 92) goes to Thorium (A = 234, Z = 90) by α -decay.
238U --> 234Th + α
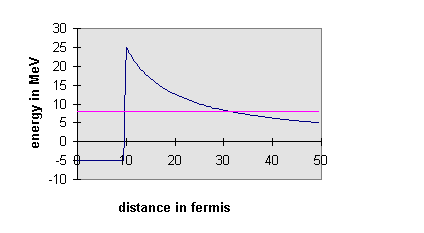The surprising thing is that for this process τ is
comparable to the age of the universe. If the decay is
energetically desirable, why does it take so long? The answer is
that there exists a potential barrier. In a simple model the
α-particle exists inside the U nucleus, confined in a deep square well
potential representing the attractive nuclear force. However, the
α-particle wave function penetrates some distance into the wall of this
finite square well potential, where the α-particle will be out of the
range of the nuclear force, but not out of the range of the long-range
electrostatic repulsive force of the other protons in the nucleus.
If the total energy of the α-particle inside the well is larger than its
potential energy outside the well, the particle can tunnel through the
barrier. There is some finite probability of finding the
α-particle shooting away from the nucleus. The actual probability
of this happening depends on the width and height of the barrier and on
the total energy of the particle. For 238U α-decay has
a half-life of over a billion years. However, many different
nuclei undergo α-decay, the quickest in millionths of a second.
Note that an alpha particle is a helium nucleus, and that both
mass number and atomic number are conserved in the decay. Alpha decay can
essentially be thought of as nuclear fission where the parent nucleus splits
into two daughter nuclei. Alpha decay is fundamentally a quantum tunneling
process. Most alpha particles are emitted with approximately 5 MeV of
kinetic energy. Virtually all of the helium produced in the United States
and elsewhere comes from trapped underground deposits associated with Uranium-
or Thorium-containing minerals which alpha decay. The Helium is brought to the
surface as a by-product of natural gas production.
Calculate the energy Q released during the alpha decay 238U -->
234Th + 4He.
The atomic masses are:
238U: 238.05079 u, 234Th: 234.04363 u,
4He: 4.00260 u.
Solution:
Show that 238U cannot spontaneously emit a proton.
Solution:
Beta decay (sometimes called neutron decay) is a type of radioactive decay in
which a β-particle or electron is emitted. A neutron alone in space will
only last about ten minutes before ejecting an electron and leaving a proton
behind. This is energetically possible, because the mass of the neutron
exceeds the sum of the masses of the proton and electron. The process is
called β-decay.
Heavier nuclei have more neutrons than protons, because
the Coulomb repulsion makes it harder to bind protons. But
neutrons are fermions and the Pauli exclusion principle requires that as
we add more and more neutrons, the energy of the added neutrons will be
higher and higher. So β-decay is often favored energetically.
In β− decay, the weak nuclear interaction converts a neutron into a proton while emitting an electron and an anti-neutrino.
n --> p + e- + νe
In β+ decay, a proton is converted into a neutron, a positron and a neutrino.
p --> n + e+ + νe
If the proton and neutron are part of an atomic nucleus the decay processes transmute one chemical element into another. The antineutrino or neutrino are near-massless particles that must be created because of conservation laws associated with elementary particle interactions.
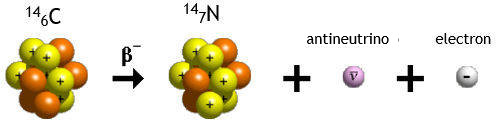
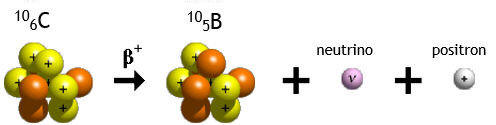
Historically, the study of beta decay provided the first
physical evidence of the neutrino. The energies of electrons
emitted in beta decay were observed to be non-discrete. Some
electrons were more energetic than others. A problem arose in
trying to explain what had happened to the missing energy if an electron
was emitted with less than the maximum energy available.
Conservation of energy appeared to be violated. Wolfgang Pauli
proposed that the "missing" energy was actually carried away by another,
yet undiscovered, particle. This was analyzed in more detail by
Enrico Fermi. Fermi called the particle the neutrino, the little
neutral one.
Detecting neutrinos is still difficult, since they are not sensitive
to the strong nuclear force or to electromagnetic fields. The
force that causes β-decay is called the weak
force. The only way to detect a neutrino is when it
collides with a particle and interacts weakly, essentially reversing one
of the β-decays. A neutrino is extremely unlikely to interact with
a nucleus, in fact a cosmic neutrino will almost certainly just pass
through the earth. It takes large detectors and a strong flux of
neutrinos to detect neutrinos. Much effort is being currently
expended detecting neutrinos from the sun, since they are our only
window into the nuclear processes taking place deep in the sun.
They can escape without interacting with the outer layers, unlike
photons or any other particle emitted.
In the radioactive decay of 238U it emits an
α-particle to become 234Th, then β-decays twice in succession
to become 234U. This nucleus is now relatively
proton-rich, and it α-decays five times in succession to become a form
of lead,
234U --> 230Th --> 226Ra
--> 222Rn --> 218Po --> 214Pb.
214Pb undergoes two β-decay, an α-decay, two β-decays, and another α-decay, before it reaches stability at 206Pb. The sequence above is through metallic elements with one exception, Radon (Rn). Radon is a noble gas and so it is chemically inert. It emits its α-particle in a period of days, which gives it time to diffuse out of the rock into somebody's basement.
| 214Pb | β- | 214Bi |
| 214Bi | β- (99.98%) | 214Po |
| 214Po | α | 210Pb |
| 210Pb | β- | 210Bi |
| 210Bi | β- (99.99987%) | 210Po |
| 210Po | α | 206Pb |
| 206Pb | is stable |
Calculate the disintegration energy Q for the beta decay 32P --> 32S + e- + ν.
Atomic masses: m(32P) = 31.97391 u, m(32S) = 31.97207 u.
Solution:
Emission of γ rays is similar to emission of photons by excited states of atoms. The nucleus can be excited by having just emitted an α- or β-particle, or by colliding with another nucleus, or by being bombarded by neutrons. All these events can lead to a nucleus which is excited, and electromagnetic radiation is emitted.
Photons with energies of more than 10 keV are often called gamma rays, although electromagnetic radiation from around 10 keV to several hundred keV is also referred to as hard x-rays. There is no physical difference between gamma rays and x-rays of the same energy, these are two names for the same electromagnetic radiation. Rather, gamma rays are distinguished from x-rays by their origin. Gamma ray is a term for high-energy electromagnetic radiation produced by nuclear transitions, while x-ray is a term for high-energy electromagnetic radiation produced by energetic electrons. Because it is possible for some electron transitions to be of higher energy than some nuclear transitions, there is an overlap between what we call low energy gamma rays and high energy x-rays Gamma-rays are a form of ionizing radiation, they are more penetrating than either alpha- or beta-radiation, but less ionizing.
Carbon has a radioactive isotope, 146C, with a half-life of 5730 years. The ratio of the abundance of this isotope to the abundance of the common 126C isotope in the air is constant (1.3*10-12). 146C is created by cosmic radiation interacting with CO2 in the air. Plants metabolize carbon, animals eat plants and create carbon compounds in their body. Fossils buried under ground are not affected by the types of cosmic radiation that creates 146C, so the ratio of 146C to 126C in fossils is slowly decreasing, because the 146C is decaying into 147N. By measuring the activity of a fossil fragment and knowing the total amount of carbon in the fragment, one can calculate the percentage of the isotope 146C in a fossil sample and deduce its age.
Chemical analysis shows that a bone fragment contains 10 g of C. Its activity is 50 counts/min = 0.833 counts/s. How old is the bone fragment?
Solution:
Is all decay harmful?
Systems decay because there is a lower energy state available. They fall into the lower energy state, and the excess energy is often carried away by a particle, for example a photon, electron, or alpha particle.
When an excited neutral atom decays, the excess energy is usually on the order of eV. This is non-ionizing radiation. When atoms in the body interact with it, the radiation does not break bonds.
When an excited nucleus decays, the excess energy is usually on the order of
MeV.
This is ionizing radiation. It breaks bonds and knocks electrons out of atoms.
How damaging radiation is depends on where it comes into contact with the body
and how deep it can penetrate in the body.
For example, 5.5 MeV alpha particles, which are charged and heavy, penetrate only about 50 micrometers. Alpha particle sources are usually not dangerous if outside the body, but are quite hazardous if ingested or inhaled, because they have about 20 times the ionization power of gamma rays with the same energy.
If you can somehow place an alpha particle sources inside a tumor, the alpha particles can effectively kill the tumor cells without affecting surrounding cells.
Gamma and X-rays can penetrate large distances, so you can focus them on a
tumor from outside the body. But they also break bonds and destroy cells
on the way in, although at a lower rate, because they energy only gets
concentrated in the focus.