There are two basic types of simple nuclear models.

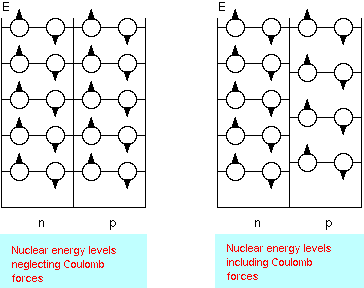
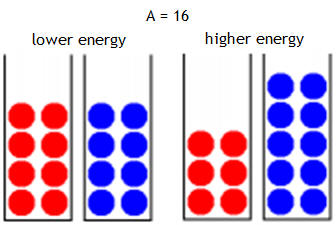
(a)  An individual particle model with nucleons in discrete energy states:

The Shell Model (developed by Maria Goeppert-Mayer and Hans Jensen), emphasizes individual particle states in the nucleus.  The Nuclear Shell Model is similar to the atomic model where electrons arrange themselves into shells around the nucleus.  The Pauli exclusion principle is responsible for a shell structure in atoms and nuclei.  The atomic shell structure is due to the quantum nature of electrons and the fact that electrons are fermions.  Since protons and neutrons are also fermions, the energy states of the nucleons are filled from the lowest to the highest as nucleons are added to the nucleus.  In the shell model the nucleons fill each energy state with nucleons in states with definite angular momentum.  There are separate energy levels for protons and neutrons.  The simplest representation is to envision neutrons and protons trapped in separate wells.  Since protons repel each other via the electric force, their energy levels are slightly higher than the corresponding energy levels of the neutrons in the same nucleus.

The ground state of a nucleus has each of its protons and neutrons in the lowest possible energy level.  Excited states of the nucleus are then described as promotions of nucleons to higher energy levels.  This model has been very successful in explaining the basic nuclear properties.  As is the case with atoms, many nuclear properties (angular momentum, magnetic moment, shape, etc.) are dominated by the last filled or unfilled valence level.

The nuclear shell model explains the existence of "magic numbers". Nuclei with magic neutron number N = 2, 8, 20, 28, 50, 82, 126 or magic proton number Z = 2, 8, 20, 28, 50, 82 have a larger binding energy per nucleon than neighboring nuclei, and when N and Z are both magic the binding energy per nucleon is especially large.  This suggests a shell structure, similar to the shell structure in atomic physics, where the noble gases have especially large ionization energies.

Problem:

¹²⁶Te (Tellurium) has 52 protons and 74 neutrons.  Is this a magic nucleus?

Solution:

• Reasoning:
  No.  Neither the proton number Z nor the neutron number N is one of the magic numbers.  The magic numbers denote filled proton or filled neutron shells.

Neutrons can convert into protons via β⁻ decay and protons can convert into neutrons via β⁺ decay.  If we add to many neutrons to a nucleus it becomes unstable and will decay via β⁻ decay.  Neutrons will decay into protons and jump from higher energy levels in the neutron well to lower energy levels in the proton well.  If we add to many protons to a nucleus it becomes unstable and will decay via β⁺ decay.  Protons will decay into neutrons and jump from higher energy levels in the proton well to lower energy levels in the neutron well.

16C decays via β⁻ decay with a half life of 0.75 s.

Embedded Question 2

• The long-range electrostatic repulsion between protons limits the size of stable nuclei.  But why are there no large nuclei consisting only of neutrons, which do not repel each other?

Discuss this with your fellow students in the discussion forum! 

(b)  A collective model with no individual particle states:

The Liquid Drop Model treats the nucleus as a liquid.  Nuclear properties, such as the binding energy, are described in terms of volume energy, surface energy, compressibility, etc, parameters that are usually associated with a liquid.  This model has been successful in describing how a nucleus can deform and undergo fission.

The Collective Model (developed by Aage Bohr and Ben Mottleson), extends the liquid drop model by including motions of the whole nucleus such as rotations and vibrations.  The Collective Model emphasizes the coherent behavior of all of the nucleons.

The Shell Model and the Collective Model represent the two extremes of the behavior of nucleons in the nucleus.  More realistic models, known as unified models, attempt to include both shell and collective behaviors.