Voltage

Charged particles exert forces on each other.  The electric field E = F/q produced by a charged particle at some position r in space is a measure of the force F the particle exerts on a test charge q, if we place the test charge at r.  The electric field E is a vector.  The electric field due to a charge distribution is the vector sum of the fields produced by the charges making up the distribution.  When we think about electricity in everyday life, we seldom think about the electric fields.  We are more familiar with the concepts of voltage, current, and power.

How is the voltage related to the electric field?

When a particle with charge q is placed in an external electric field E, (i.e. an electric field produced by other charges), then an electric force F = qE will act on it.  If this force is not balanced by other forces, then the particle will accelerate, and its kinetic energy will change.  The electric force will do positive work on the particle.  If the electric force is balanced by another external force F_ext = -qE, and if this external force moves the particle against the electric force, than the external force F_ext does positive work. 

Recall!

• The work W done on an object by a constant force is defined as W = F∙d = F d cosθ.  Here F is the magnitude of the force, d is the magnitude of the displacement vector, and θ is the angle between the directions of the force and displacement vectors.
  The work done by a varying force in one dimension is defined as W = Σ_xi^xf F_x∆x, as ∆x becomes infinitesimally small.  In three dimensions we write
  W = Σ F∙∆r = Σ_xi^xf F_x∆x +  Σ_yi^yf F_y∆y + Σ_zi^zf F_z∆z.
   

Therefore the work done done by an external force balancing the electric force is

W = Σ F_ext∙∆r = -q Σ E∙∆r.

In the sums we always assume that the displacements become infinitesimally small.

The work done by the external force F_ext = -qE is equal to the change in the electrostatic potential energy of the particle in the external field.  The change in the potential energy of a charge q when being moved from point A to point B, is the work done by F_ext in moving the charge.

∆U = U_B - U_A = -q Σ_A^B E∙∆r.

The sum is taken along a particular path.  But the electrostatic force is a conservative force.  The work is independent of the path.  ∆U therefore depends only on the endpoints A and B of the path, not on the actual path itself.

Embedded Question 1

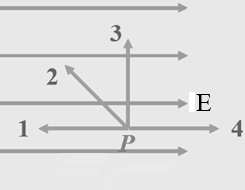
(a)  Which requires zero work, to move a positive point charge from point P to point 1, 2, 3, or 4?   All those points are the same distance from P.
(b)  Which requires the most positive work done by an external force, to move a positive point charge from point P to point 1, 2, 3, or 4?

Discuss this with your fellow students in the discussion forum!
Review the concept of work in physics.
Discuss the relationship between the work done by and against the electric field and the electrostatic potential energy.

The change in potential energy is proportional to the charge q.  Its sign depends on whether the charge is positive or negative.  We define the potential difference or voltage ∆V as the potential energy difference divided by the charge, or the potential energy difference per unit (positive) charge. 

∆V = V_B - V_A = -Σ_A^B E∙∆r.

The potential difference is the potential energy difference of a small, positive test charge, divided by the charge.  As in the case of gravity, the zero of the potential energy and therefore the zero of the potential are not uniquely defined.  Only potential energy differences and potential differences are unique.  The SI unit of energy is J, therefore the SI unit of potential is J/C.  We define Volt as V = J/C.

The electrostatic potential is a scalar, not a vector.

We say that a charge distribution, which produces an electric field, also produces an electric potential.  The electrostatic potential produced by a finite charge distribution is, by convention, set to zero at infinity.  Then the potential V(r) of the distribution is the work done per unit charge in bringing a small test charge from infinity to position r.  For a charge distributions which extend to infinity, we cannot set the zero of the potential at infinity, because then the potential would be infinite everywhere, and it would be a useless concept.  We then set the zero at some convenient reference point, but we always must specify the reference point along with the potential, since there is no unique convention.  For many applications we choose the ground to be the zero of the potential.

The potential difference between the two terminals of an A, B, C, or D cell battery is 1.5 V.  For every Coulomb of negative charge that is moved from the positive to the negative terminal, 1.5 J of work must be done against electric forces, and 1.5 J of some other form of energy is converted into electrostatic energy.  When the terminals are connected by a wire, then the charge is free to move inside the wire, and the electric field does work on the charge.  This work can now be reconverted into some other form of energy.

The potential at a point r of a positive point charge located at the origin is the work that must be done per unit charge in bringing a test charge from infinity to r.

V(r) = -Σ_∞^r E∙∆r = Σ_r^∞ E∙∆r .

We can bring the test charge along an arbitrary path, which we can think of as being made up of infinitesimal small steps, either in the radial direction or perpendicular to the radial direction.  We do not have to do work when we step perpendicular to the radial direction, because then E is perpendicular to ∆r.  Along the radial direction E∙∆r = E∆r, because E and r points both point outward.  The sum becomes

V(r) = q/(4πε₀r) = k_eq/r.

This expression also gives the potential due to any spherically symmetric charge distribution outside the distribution.

The potential outside a spherically symmetric charge distribution with total charge q is the same as that of a point charge q, V(r) = k_eq/r.
It is is proportional to the inverse of the distance from the point charge.

To find the potential due to a collection of charges, we use the principle of superposition and add the potentials due to the individual charges.  Because the potential is a scalar, and not a vector, we just have to add numbers.  To find the total electrostatic potential energy of a collection of point charges, sum over all pairs.

Problem:

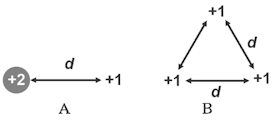The charges in the groups A and B below are all given in units of Q. Which group of charges took less work by an external force to bring together from infinity?

Solution:

• Reasoning:
  For case A:
  We have only one pair of charges.
  W = k_e 2Q*Q/d = 2 k_eQ²/d.
  
  For case B:
  We have 3 pairs of charges.
  Bring the two lower charges together: W = k_e Q²/d.
  Bring the top charge:
  Do work against the force exerted by the two lower charges
  W = k_e Q²/d + k_e Q²/d = 2 k_e Q²/d.
  Total Work: W = 3 k_eQ²/d = sum over all pairs.
  
  Group A took less work by an external force to bring together from infinity than group B.

Units:

1 electron volt (eV)  = 1.6*10^-19 J.

1 eV is the change in potential energy of a particle with charge q_e = 1.6*10^-9 C  when the change in potential is 1 Volt (V).  The unit was defined so that when you know the voltage between two points in space, you know the change in potential energy of an elementary particle when it moves from one to the other point.  (The sign of the change in potential energy depends on the sign of the charge.)  When a free proton moves through a potential difference of 1 V its kinetic energy decreases by -qV = (1.6*10^-19 C)*(1 J/C) = -1.6*10^-19 J = -1 eV.  When a free electron moves through the same potential difference of 1 V its kinetic energy increases by -qV = -(-1.6*10^-19 C)*(1 J/C) = 1.6*10^-19 J = 1 eV.

Problem:

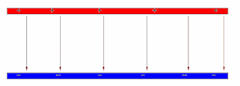Assume that the potential difference between the positive and negative plate is 100 V.  A proton travels from the positive to the negative plate.  What happens to the proton's kinetic energy?

Solution:

• Reasoning:
  The electrostatic force is a conservative force.
  ∆KE + ∆U = 0.
  (change in kinetic energy + change in potential energy = 0.)
• Details of the calculation:
  The proton accelerates towards the negative plate.  Its potential energy decreases by 100 eV.
  Its kinetic energy increases by 1.6*10^-17 J = 100 eV.

Summary:

By definition, the potential difference is the potential energy difference of a small, positive test charge, divided by the charge. The zero of the potential energy and therefore of the potential is not uniquely defined, but chosen at a convenient place.  Voltage is just another word for potential difference, or potential energy difference divided by the charge.
∆V = ∆U/q.

A particle always accelerates towards the position with the lower potential energy U.  The electrostatic potential energy is U = qV, were V is the potential. Consider a particle with charge of magnitude q_e, for example a proton (+q_e) or and electron (-q_e).

If q = q_e, then U = q_eV.  U gets more positive or higher, the bigger V.  The positively charged particle accelerates towards the region of lower potential.

If q = -q_e, then U = -q_eV.  U gets more negative or lower, the bigger V.  The negatively charged particle accelerates towards the region of higher potential.

If the potential difference is V, the change in potential energy of the particle U can be calculated in SI units.  But the nice thing about the unit eV is, that if the voltage difference is given in volts V, then the change in the potential energy of the particle, ±q_eU, is just the same number in units of eV.

Equipotential surfaces

Just as we described the electric field around a charged object by field lines, we can also describe the electric potential pictorially with equipotential surfaces (contour plots).  Each surface corresponds to a different fixed value of the potential.  Equipotential lines are lines connecting points of the same potential.  They often appear on field line diagrams. 

Equipotential lines are always perpendicular to field lines.

The electric potential at a position r is the electric potential energy a charge q has if it is at position r.  As the name equipotential implies, the potential energy of a charge would be the same anywhere on an equipotential surface.  If the charge moved along an equipotential surface, its electric potential energy would not change, no work would be done by or against the electric field.  But if there was a component of the electric field tangent to the equipotential surface, then, if the charge moved along that component, the electric field would do work and the potential energy of the charge would change.  This is a contradiction. We cannot have a component of the electric field tangent to an equipotential surface.  Hence, any electric field must be perpendicular to any equipotential surface.
 

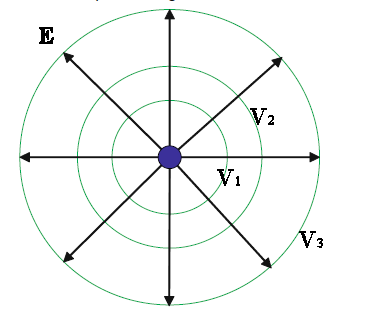Example:

Field lines and equipotential lines for a positive point charge are shown in the figure.  This is a 2-dimensional representation, a cut through the 3-d surfaces.
Please also explore this 3-dimensional representation below.   Please click on the image!

Problem:

In the Bohr model of the hydrogen atom, the electron orbits the proton at a distance of r = 5.29*10^-11 m.  The proton has charge +q_e and the electron has charge -q_e, where q_e = 1.6*10^-19 C.  How much work must be done to completely separate the electron and the proton

Solution:

• Reasoning:
  The force on the electron is the Coulomb force between the proton and the electron.  It pulls the electron towards the proton.  For the electron to move in a circular orbit, the Coulomb force must equal the centripetal force.  We need k_eq_e²/r² = mv²/r.
• Details of the calculation:
  mv² = k_eq_e²/r, so the kinetic energy of the electron is
  KE(r) = ½mv² = ½k_eq_e²/r.
  The potential energy of the electron in the field of the positive proton point charge is U(r) = -q_eV(r) = - k_eq_e²/r. 
  The total energy is the sum of the electron's kinetic energy and its potential energy.
  KE(r) + PE(r) = -½k_eq_e²/r = (-½) (9*10⁹)(1.60*10^-19) /(5.29*10^-11) J = -2.18*10^-18 J.
  This is usually stated in energy units of electron volts (eV).  1 eV = 1.60*10^-19 J.
  -2.18*10^-18 J * 1eV/(1.60*10^-19 J) = -13.6 eV.
  To remove the electron from the atom, i.e. to move it very far away and give it zero kinetic energy, 13.6 eV of work must be done by an external force. 
  13.6 eV is the ionization energy of hydrogen.

Problem:

An alpha particle containing two protons is shot directly towards a platinum nucleus containing 78 protons from a very large distance with a kinetic energy of 1.7*10^-12 J.  What will be the distance of closest approach?

Solution:

• Reasoning:
  The electric charge of the alpha particle is q₁ = 2q_e and that of the platinum nucleus is q₂ = 78 q_e.  The alpha particle and the nucleus repel each other.  As the alpha particle moves towards the nucleus, some of its kinetic energy will be converted into electrostatic potential energy.  At the distance of closest approach, the alpha particle's velocity is zero, and all its initial kinetic energy has been converted into electrostatic potential energy.
• Details of the calculation:
  The initial kinetic energy of the alpha particle is KE = 1.7*10^-12 J.
  The final potential energy is U = kq₁q₂/d, where d is the distance of closest approach.
  We have k_eq₁q₂/d = 1.7*10^-12 J.  This yields
  d = k_eq₁q₂/(1.7*10^-12 J) = (9*10⁹*2*78*(1.6*10^-19)²/(1.7*10^-12)) m = 2.1*10^-14 m
  for the distance of closest approach.  The alpha particle's velocity is zero at d.
  The acceleration is in a direction away from the nucleus.  The distance between the alpha particle and the nucleus will increase again, converting the potential energy back into kinetic energy.

Problem:

An evacuated tube uses a voltage of 5 kV to accelerate electrons from rest to hit a phosphor screen.
(a)  How much kinetic energy does each electron gain?
(b)  What is the speed of an electron when it hits the copper plate?

Solution:

• Reasoning:
  1 eV is the change in potential energy of a particle with charge q_e = 1.6*10^-9 C  when the change in potential is 1 Volt (V).
• Details of the calculation:
  (a)  Each electron loses 5 keV of potential energy and gains 5 keV = (5000 eV)(1.6*10^-19 J/eV) = 8*10^-16 J of kinetic energy.
  (b)  E = ½m_ev².  v² = 2E/m_e = (2*8*10^-16 J)/(9.1*10^-31 kg) = 1.75*10¹⁵ (m/s)².
  v = 4.2*10⁷ m/s.  This is more than 1/10 the speed of light.

The electrostatic potential V is related to the electrostatic field E.  If the electric field E is known, the electrostatic potential V can be obtained using V(r) = -Σ_∞^r E∙∆r.

How can we obtain the field from the potential?

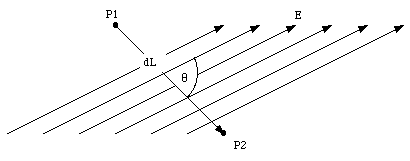
Consider the two points P₁ and P₂ shown in figure above.  Assume that they are separated by an infinitesimal distance ∆L.  The change in the electrostatic potential between P₁ and P₂ is given by ∆V = -E∙∆L = -E ∆L cosθ.   Here θ is the angle between the direction of the electric field and the direction of the displacement vector ∆L.  We can rewrite this equation as

∆V/∆L = -E cosθ = -E_L.
E_L indicates the component of the electric field along the direction of ∆L.  If the direction of the displacement is chosen to coincide with the x-axis, this becomes

∆V/∆x = -E_x.
For the displacements along the y-axis and z-axis we obtain ∆V/∆y = -E_y and ∆V/∆z = -E_z.
The total electric field E can be obtained from the electrostatic potential V by combining these three equations. 
We say that E is the negative gradient of the potential V.

In many electrostatic problems the electric field due to a certain charge distribution must be evaluated.  The calculation of the electric field can be carried out using two different methods:

• The electric field can be calculated by applying Coulomb's law and vector addition of the contributions from all charges in the charge distribution.
• The total electrostatic potential V can be obtained from the algebraic sum of the potential due to all charges that make up the charge distribution, and the field can be found by calculating the gradient of V.

In many cases the second method is simpler, because the calculation of the electrostatic potential involves an algebraic sum, while the direct calculation of the field involves a vector sum.

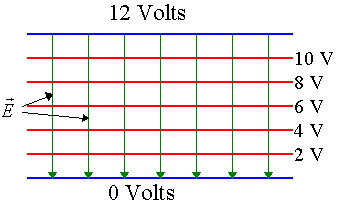Problem:

The potential difference between the two plates of the capacitor shown below is 12 V.  Equipotential surfaces are shown.  If the separation between the plates is 1 mm, what is the strength of the electric field between the plates?

Solution:

• Reasoning:
  Let the y-axis point upward.  V only varies with y.  ∆V/∆x = ∆V/∆z = 0.  E = E_y j = -∆V/∆y  j.
• Details of the calculation:
  Let the y-axis point upward.  The field is uniform and points in the negative y-direction. 
  ∆V/∆y = -E_y = (12 V)/(10^-3 m).  E_y = -12000 V/m.
  The strength of the electric field between the plates is E = 12000 V/m = 12000 N/C.

Problem:

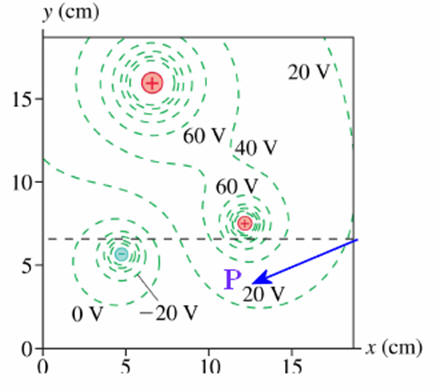The graph on the right shows a contour map of the equipotential surfaces due to 3 point charges.  Estimate the magnitude and direction of the electric field at point P.

Solution:

• Reasoning:
  Point P lies between two equipotential surfaces.  The surface above P is at 40 V and the surface below is at 20 V.  The electric field points away from the positive charge, from higher to lower potential.  It points downward at P.
  Given the distance scale, I estimate the perpendicular distance between the 40 V and 20 V equipontential surfaces near point P to be 2.5 cm.
• Details of the calculation:
  |E| = ∆V/∆y = 20 V/ 2.5*10^-2 m = 800 V/m.
  The magnitude on of the electric field at point P is ~800 V/m and it points downward.

If you miss having regular lectures, consider this video lecture