Series and parallel capacitors

A capacitor is a device for storing separated charge and therefore storing electrostatic potential energy.  Circuits often contain more than one capacitor.

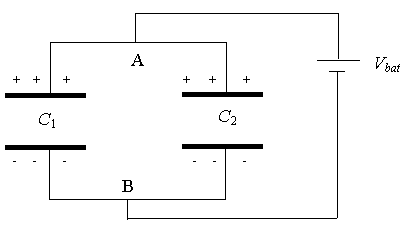two capacitors in parallelConsider two capacitors in parallel as shown on the right

When the battery is connected, electrons will flow until the potential of point A is the same as the potential of the positive terminal of the battery and the potential of point B is equal to that of the negative terminal of the battery.  Thus, the potential difference between the plates of both capacitors is VA - VB = Vbat.  We have C1 = Q1/Vbat and C2 = Q2/Vbat, where Q1 is the charge on capacitor C1, and Q2 is the charge on capacitor C2.  Let C be the equivalent capacitance of the two capacitors in parallel, i.e. C = Q/Vbat, where Q = Q1 + Q2.  Then C = (Q1 + Q2)/Vbat = C1 + C2.

For capacitors in parallel, the capacitances add.

For more than two capacitors we have

C = C1 + C2 + C3 + C4 + ... .

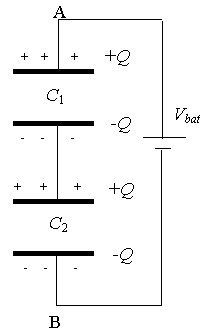two capacitors in seriesConsider two capacitors in series as shown on the right.

Let Q represent the total charge on the top plate of C1, which then induces a charge -Q on its bottom plate.  The charge on the bottom plate of C2 will be -Q, which in turn induces a charge +Q on its top plate as shown.
Let V1 and V2 represent the potential differences between plates of capacitors C1 and C2, respectively.  Then V1 + V2 = Vbat, or (Q/C1) + (Q/C2) = Q/C, or (1/C1) + (1/C2) = 1/C.  For more than two capacitors in series we have

1/C = 1/C1 + 1/C2 + 1/C3 + 1/C4 + ... .

where C is equivalent capacitance of the two capacitors.

For capacitors in series the reciprocal of their equivalent capacitance equals the sum of the reciprocals of their individual capacitances.

Problem:

What total capacitances can you make by connecting a 5 μF and an 8 μF capacitor together?

Solution: