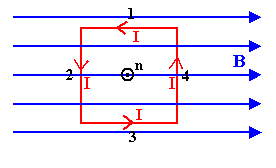
A current I is flowing in a square loop.  The sides of the square have length L.  Let the direction of the normal to the loop be defined by the right-hand rule.  Curl the fingers of your right hand in the direction of the current flow.  Your thumb points into the direction of the normal.  Assume that the square loop is placed into a magnetic field and that the normal to the area is perpendicular to B as shown on the right.

The force on each side is given by F = IL × B.  The current I is the same for each side, but the vector L is different for each side.  The force on sides 1 and 3 is zero, since L × B is zero.  The force on side 2 has magnitude F = ILB and points out of the page. The force on side 4 has magnitude F = ILB and points into the page.  The total force is zero.  

In a uniform magnetic field the net force on a current loop is zero.

But each of the non-zero forces has a lever arm about the center of the loop, and therefore exerts a torque τ = (L/2)F about the center of the loop.  (The torque exerted by a force F about a point P is τ = r × F, where r is the vector pointing from P to the point where the force is applied.)  The total torque is τ = LF = IL²B, lying in the plane of the page and pointing upward.

In a uniform magnetic field the total torque on a current loop is, in general, NOT zero.  The torque tries to align the normal to the area of the loop with the magnetic field.

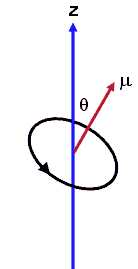For a current loop we have defined the magnetic moment μ as

μ = IAn.
(magnetic moment = current times area)

The torque on a current loop can then be written as τ = μ × B.  
The magnitude of the torque is τ = μB sinθ.  The torque tries to align μ and B.

A magnetic dipole is a current loop whose area goes to zero, or, for practical purposes, a current loop whose dimensions are very small compared to all the other dimensions important in the problem.  In a uniform magnetic field the net force on a magnetic dipole is zero, but the torque is not zero, unless the dipole is aligned or anti-aligned with the magnetic field.

If a magnetic dipole μ is aligned with an external magnetic field B, an external force has to do work to change the angle between μ and B from 0 to some angle θ.  The magnetic dipole gains potential energy.  The potential energy U_μ of a magnetic dipole in an external field B is

U_μ = -μB cosθ.

The potential energy is lowest when the dipoles is aligned (θ = 0) with the field and highest when it is anti-aligned  (θ = π).  The zero of U_μ is arbitrarily chosen at π/2, since only potential energy differences are important.

Problem:

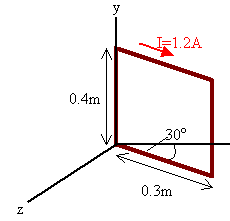A rectangular loop consists of N = 100 closely wrapped turns and has dimensions a = 0.4 m and b = 0.3 m.  The loop is hinged along the y-axis and its plane makes an angle of 30^o with the x-axis. What is the magnitude of the torque exerted on the loop by a uniform magnetic field B = 0.8 T directed along the x-axis when the current I is 1.2 A in the direction shown?
What is the expected direction of rotation of the loop?

Solution:

• Reasoning:
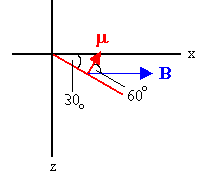
  The torque exerted on the loop is τ = μ × B.  The magnetic moment is the magnetic moment per turn, times the number of turns, μ = NabI.  The direction of μ makes an angle of 60^o with the x-axis.  The smallest angle between μ and B is 60^o.
• Details of the calculation:
  The magnitude of the torque is
  τ = N ab IB sin60^o= 100(0.4)(0.3)(1.2)(0.8)(0.866) Nm = 9.98 Nm.
  The torque is in the negative y-direction.  It tries to rotate the loop clockwise in the diagram.  It tries to align μ and B.

Embedded Question 2

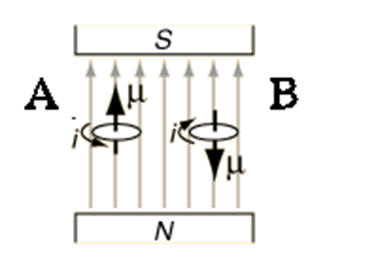
Consider the loops in the figure on the right.  Which statement is false?

1. There is no net force acting on either loop.
2. Loop A has lower potential energy than loop B.
3. There is no torque acting on loop A but a torque is acting on loop B.
4. Loop A is in stable equilibrium and loop B is in unstable equilibrium.

Discuss this with your fellow students in the discussion forum!
What is the energy of a magnetic dipole in a magnetic field?

A simple DC electric motor consists of a wire-wound rotor mounted on an axle between the pole faces of a permanent magnet.

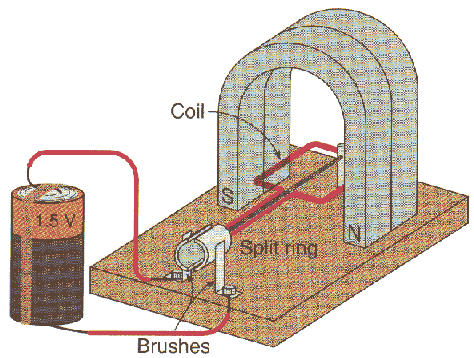The magnetic field between the pole faces is nearly uniform, pointing from the north pole towards the south pole of the magnet.  When a current flows through the wire loop of the rotor, a torque tries to align the magnetic moment of the loop with the magnetic field.  The torque produces angular acceleration.  When μ and B are aligned the torque is zero, but the loop has angular velocity and angular momentum.  It therefore overshoots the aligned position.  A split ring causes the current to reverse direction in the loop, just as it passes the aligned position.  This reverses the direction of the magnetic moment μ.  The torque again tries to align μ and B by accelerating the loop through another 180^o degree turn.  Then the current reverses its direction again, etc.  The split-ring configuration is a crucial feature of a DC motor.  It is called a split-ring commutator.

External link:
DC motor principle  (Youtube)

If you miss having regular lectures, consider this video lecture.