Faraday's law is one of Maxwell's equations.  Faraday's law states that the absolute value or magnitude of the circulation of the electric field E around a closed loop is equal to the rate of change of the magnetic flux through the area enclosed by the loop.  The equation below expresses Faraday's law in mathematical form.

ΔΦ_B/∆t (through a fixed area) = -Σ_{around loop} E∙∆r (at a fixed time)

The minus sign in this equation tells us about the direction of the circulation.  (See below.)

When the magnetic flux through the area enclosed by the loop changes, Σ_{around loop} E∙∆r is not zero, the electric field E circulates.
E∙∆r is the work done per unit charge by the electric field in moving the charge a distance ∆r.
If the loop is an actual wire loop, then there is actual work done by the induced field on free charges. 
Σ_{around loop} E∙∆r is the work per unit charge by the field in moving the charge once around the loop.
This is an induced emf, and it is measured in Volts.
The induced emf causes a current to flow without a potential difference due to separated charges.

ΔΦ_B/∆t (through a fixed area) = induced emf

The induced electric field is NOT a conservative field.  When you move a charge against the induced field once around the loop, you have to do work.  But your work is NOT stored as potential energy.  You cannot let the electric field do work to recover the energy you expended in moving the charge.  The induced electric field disappears as soon as the magnetic flux is no longer changing.  The work you do on a charge against the induced field is not locally stored.  The energy may be transported away in the form of an electromagnetic wave.  Electromagnetic waves carry energy through free space.

What is the direction of the dynamic (induced) field?

The minus sign in the equation expressing Faraday's law tells us about the direction of the induced field. 
There is an easy way to remember this direction.  The circulation of the induced field is equal to an emf. 
Any current flowing as the result of that emf produces a magnetic field that opposes the flux changes that produce it. 
This is called Lenz's law. 

An induced emf acts as to oppose the CHANGE in flux that produce it.

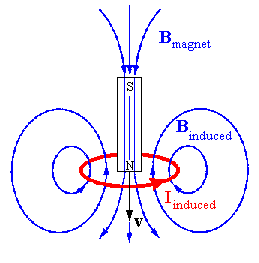
Example:

A magnet is moved quickly towards a wire loop as shown.
The flux through the wire loop is increasing in the downward direction. 
A current starts flowing in the loop in the direction indicated by the arrow. 
The magnetic field produced by this current points upward, it opposes the flux changes that produce it.
The magnetic force due to the loop on the magnet acts to slow down the approaching magnet.

The beauty of Lenz's law is that you do not have to look at the details. If the magnetic flux through a conductor changes, currents will flow to oppose whatever caused the change. If some relative motion causes a flux change, the current will try to stop that relative motion.  If a change in a current in a circuit is responsible for the flux change, then the induced emf will try to prevent the change in the current of that circuit.

Please watch:  Electromagnetic Induction and Faraday's Law (Youtube)

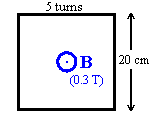
Problem:

Consider a flat square coil with N = 5 loops. 
The coil is 20 cm on each side, and has a magnetic field of 0.3 T passing through it.
The plane of the coil is perpendicular to the magnetic field: the field points out of the page.
(a)  If nothing is changed, what is the induced emf?
(b)  The magnetic field increases uniformly from 0.3 T to 0.8 T in 1 s.  While the change is taking place, what is the induced emf in the coil?
(c)  While the magnetic field is changing, the emf induced in the coil causes a current to flow.  Does the current flow clockwise or counter-clockwise around the coil?

Solution:

• Reasoning:
  If the magnitude of the magnetic field B changes, then the flux Φ = BA changes, and an emf is induced.
• Details of the calculation:
  (a)  An emf is induced by a changing magnetic flux.  If nothing changes, the induced emf is zero.
  (b)  The coil has 5 turns.  Each turn has area A = (0.2 m)².  The initial magnetic flux through each turn of the the coil is Φ₀ = B₀A = 0.3*(0.2)² Tm² = 0.012 Tm².
  The final magnetic flux through each turn of the coil is Φ_f = B_fA = 0.8*(0.2)² Tm² = 0.032 Tm².
  The total change of the flux through the coil N(Φ_f - Φ₀), with N = 5.  The induced emf is
  emf = -N∆Φ/∆t = -N(Φ_f - Φ₀)/∆t = [-5*(0.032  -0.012)/1.0] V = -0.1 V.
  (c)  While the magnetic field is changing, the magnetic flux increased out of the page.  According to Lenz's law, the emf induced in the loop by this changing flux produces a current that sets up a field opposing the change.  The field set up by the current in the coil, points into the page, opposite to the direction of the increase in flux.  To produce a field into the page, the current must flow clockwise around the loop according to the right-hand rule.

Embedded Question 1

A bar magnet is positioned in front of a horizontal loop of wire with its north pole pointing toward the loop. Then the magnet is pulled away from the loop.  Does the induced current in the loop flow clockwise or counterclockwise?

Discuss this with your fellow students in the discussion forum!
Visualize the magnetic field of a bar magnet.  How does the flux of this field through the wire loop change?

Self induction

If a long coil of wire of cross sectional area A and length ℓ with N turns is connected or disconnected from a battery, the changing magnetic flux through the coil produces an induced emf.  The induced current produces a magnetic field, which opposes the change in the magnetic flux.  The magnitude of the induced emf can be calculated using Faraday's law.

• The magnetic field inside the long coil is B = μ₀(N/ℓ)I.
• The flux through the coil is NBA = μ₀(N²/ℓ)IA.
• The change in flux per unit time is μ₀(N²/ℓ)A ∆I/∆t = L*∆I/∆t, since I is the only quantity changing with time.
  L = μ₀(N²/ℓ)A is called the self inductance of the coil.  The units of inductance are Henry (H).  1 H = 1 Vs/A.
• The induced emf is emf = -L*∆I/∆t, where the minus sign is a consequence of Lenz's law.

The induced emf is proportional to the rate of change of the current in the coil.  It can be several times the power supply voltage.  When a switch in a circuit carrying a large current is opened, reducing the current to zero in a very short time interval, this can result in a spark.  All circuits have self inductance, and we always have emf = -L*∆I/∆t.  The self inductance L depends only on the geometry of the circuit.

Problem:

A coil has an self inductance of 3 mH, and a current through it changes from 0.2 A to 1.5 A in a time of 0.2 s.  Find the magnitude of the average induced emf in the coil during this time.

Solution:

• Reasoning:
  The emf due to self induction is emf = -L*∆I/∆t.
• Details of the calculation:
  L = 3 mH,  ∆I/∆t = (1.5 A - 0.2 A)/0.2 s = 6.5 A/s.
  emf = -L*∆I/∆t = -(0.003 Vs/A)(6.5 A/s) = -0.0195 V.
  The minus sign indicates that the induced emf opposes the flux changes that produced it.

Problem:

A 25 turn circular coil of wire has a diameter of 1 m.  It is placed with its axis along the direction of the Earth's magnetic field (magnitude 50 microT), and then, in 0.2 s, it is flipped 180^o.  What is the average emf generated

Solution:

• Reasoning:
  Φ_B = B∙A is the flux of B through the area A.  Initially B and A are aligned, finally they are anti-aligned.  The dot product changes sign.
• Details of the calculation:
  emf = -∆Φ_B/∆t. Φ_B(initial) = NAB = 25*π*(0.5 m)²50*10^-6 T = 9.82*10^-4Tm².
  Φ_B(final)  = -Φ_B(initial) since the coil is flipped.
  |∆Φ_B| = 2Φ_B(initial).
  |∆Φ_B/∆t| = 2*(9.82*10^-4 Tm²)/(0.2 s) = 9.82*10^-3 V.

Problem:

A 0.5 m radius, 500-turn coil is rotated one-fourth of a revolution in 4.17 ms, originally having its plane perpendicular to a uniform magnetic field.  Find the magnetic field strength needed to induce an average emf of 10,000 V.

Solution:

• Reasoning:
  emf = -∆Φ_B/∆t.  Φ_B = NABcosθ changes from NAB to 0 in 4.17 ms, since θ changes from 0 to 90^o in 4.17 ms.
• Details of the calculation:
  |∆Φ_B| = NAB = 500*π*(0.5 m)²*B = (393 m²) * B.
  We want
  |emf| = |∆Φ_B/∆t| =  (393 m²)/(4.17*10^-3 s) * B = (94174 m²/s)*B = 10000 V.
  B = 0.1 Vs/m² = 0.1 T.

If you miss having regular lectures, consider this video lecture.