When a battery charges a parallel-plate capacitor, the battery does work separating the charges.  If the battery has moved a total amount of charge Q by moving electrons from the positively charged plate to the negatively charged plate, then the voltage across the capacitor is V = Q/C and the amount of work done by the battery is W = ½CV².  The battery has converted chemical energy into electrostatic potential energy.

Where is this energy stored?

We can view the energy U as being stored in the separated charges,
U = ½Q²/C.

We can also view the energy as being stored in the electric field produced by the separated charges,
U = ½CV².

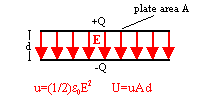Let the area of the plates of the parallel-plate capacitor be A and the plate separation be d.
Then V = Ed and C = ε₀A/d.  We can therefore write
U = ½ε₀E²(A*d).

(A*d) is the volume between the plates of the capacitor.  Inside this volume the electric field is approximately constant and outside of this volume the electric field is approximately zero.

We interpret u_E = ½ε₀E² as the energy density, i.e. the energy per unit volume, in the electric field.  The energy stored between the plates of the capacitor equals the energy per unit volume stored in the electric field times the volume between the plates.

In electrostatics, viewing the energy as being stored in the separated charges or viewing it as being stored in the electric field leads to the same results.  We are allowed to take either point of view.

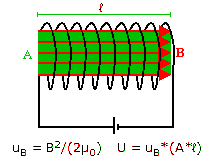Assume you connect a battery to a coil with cross sectional area A, length ℓ, and n turns per unit length.  Assume that the coil has resistance R.  After some time a steady current I_f will flow through the coil, I_f = V/R, where V is the battery voltage.  But just after you connect the battery, when the current begins to flow and the magnetic flux through the coil begins to change, an induced emf = -L*∆I/∆t will oppose the current flow, where L is the self inductance of the coil.  The battery has to do work against this induced emf.  The amount of work done per unit time against the induced emf, i.e. the power supplied by the battery to overcome the induced emf, is
∆W/∆t = |emf|*I = (L*∆I/∆t)*I. 

This is the rate at which the battery converts chemical energy into magnetic energy.
Multiplying both sides of the equation by ∆t, we can write ∆W = L*I*∆I.
The total amount of energy converted is W = L*I_avg*(I_f - I_i).
Since I_i = 0, we have I_avg = (I_f + I_i)/2 = I_f/2, and W = ½LI_f².

We can view this energy as being stored in the circulating current,
U = ½LI_f².

But we can also view the energy as being stored in the magnetic field.
For the self inductance of a coil we have L = (μ₀n²Aℓ).  The magnetic field inside the coil is approximately B = μ₀nI.  We may therefore write I = B/(μ₀n), and
U = ½(μ₀n²Aℓ)*(B/(μ₀n))² = (B²/(2μ₀))(A*ℓ).

(A*ℓ) is the volume surrounded by the coil.  Inside this volume the magnetic field is approximately constant and outside of this volume the magnetic field is approximately zero.

We interpret u_B = B²/(2μ₀) as the energy density, i.e. the energy per unit volume, in the magnetic field.  The energy stored in the volume surrounded by the coil equals the energy per unit volume stored in the magnetic field times the volume surrounded by the coil.

In magnetostatics, viewing the energy as being stored in the circulating currents or viewing it as being stored in the magnetic field leads to the same results.  We are allowed to take either point of view.

Problem:

A MRI machine produces a magnetic field of magnitude 1.5 T in a cylindrical volume of radius r = 0.4 m and length L = 1.25 m.  How much energy is stored in the magnetic field in this volume?

Solution:

• Reasoning:
  The energy stored in the magnetic field is given by U = u_BV = (B²/(2μ₀))V = (B²/(2μ₀)(A*ℓ).
  B²/(2μ₀) is the energy per volume and A*ℓ is the cylindrical volume.
• Details of the calculation:
  Here B = 1.5 T, L = 1.25 m and A = π*(0.4 m)², 2μ₀  = 8π*10^-7 N/A².
  Energy stored = (1.5 T)²*(1.25 m)*π*(0.4 m)²/(8π*10^-7 N/A²) = 5.62*10⁵ J.
  (5.62*10⁵ J*(1 kWh/3.6 * 10⁶ J) = 0.156 kWh.

In electrodynamics we take the view that electromagnetic energy is stored in the electric and magnetic fields.
Electromagnetic waves can transport this field energy through space.  Electromagnetic waves are changing electric and magnetic fields, carrying energy through space.