• A charged particle produces an electric field.  This electric field exerts a force on other charged particles.  Positive charges accelerate in the direction of the field and negative charges accelerate in a direction opposite to the direction of the field.
• A moving charged particle produces a magnetic field.  This magnetic field exerts a force on other moving charges.  The force on these charges is always perpendicular to the direction of their velocity and therefore only changes the direction of the velocity, not the speed.
• An accelerating charged particle produces an electromagnetic (EM) wave.  Electromagnetic waves are electric and magnetic fields traveling through empty space with the speed of light c.  A charged particle oscillating about an equilibrium position is an accelerating charged particle.  If its frequency of oscillation is f, then it produces an electromagnetic wave with frequency f.  The wavelength λ of this wave is given by λ = c/f.  Electromagnetic waves transport energy through space. This energy can be delivered to charged particles a large distance away from the source.

Accelerating charges produce changing electric and magnetic fields.  Changing electric fields produce magnetic fields and changing magnetic fields produce electric fields.  This interplay between induced electric and magnetic fields leads to propagating electromagnetic waves.  Electromagnetic waves can propagate through free space. 

Assume a charge q located near the origin is accelerating.  It therefore produces electromagnetic radiation.  At some position r in space and at some time t, the electric field of the electromagnetic wave produced by the accelerating charge is given by

E_rad(r,t) = -[1/(4πε₀)]*[q/(c²r')]*a_perp(t - r'/c).

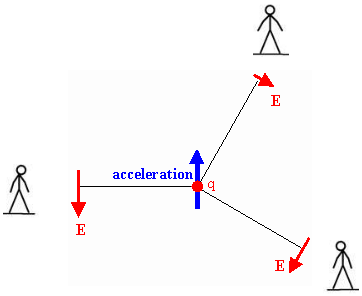Let us analyze this expression.  The electric field is proportional to the charge q.  The bigger the accelerating charge, the bigger is the field.  It decreases as the inverse of the distance r', which is the distance between the accelerating charge and the position where the field is observed.  But it is not the distance at the time the field is observed, but the distance at some earlier time, called the retarded time, when the radiation field was produced.  All electromagnetic waves travel with the speed of light c = 3*10⁸ m/s in free space.  It takes them a time interval ∆t = ∆r/c to travel a distance ∆r.  The electric field is also proportional to the acceleration of the charge.  The larger the acceleration, the larger is the field.  In the above expression E_rad(r,t) is proportional to a_perp, the component of the acceleration perpendicular to the line of sight between r and the retarded position of the charge.  The direction of E_rad(r,t) is  perpendicular to this line of sight and its magnitude is proportional to the component of the acceleration perpendicular to this line of sight. 

The figure on the right illustrates that point.  The electric field is zero along a line of sight in the direction of the acceleration, largest along a line of sight perpendicular to the direction of the acceleration, and always perpendicular to the line of sight.

The magnitude of a_perp is a*sinθ, and the magnitude of the radiation field therefore is
E_rad(r,t) = -[1/(4πε₀)]*[q/(c²r)]*sinθ*a(t - r/c).
Here θ is the angle between the line of sight and the direction of the acceleration.

The magnetic field of the electromagnetic wave is perpendicular to the electric field and has magnitude B_rad = E_rad/c in free space.  For electromagnetic waves E and B are always perpendicular to each other and perpendicular to the direction of propagation.  The direction of propagation is the direction of E × B.

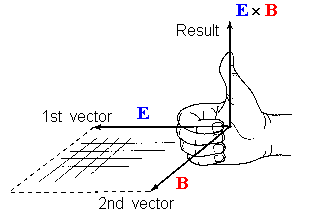
The radiation field E_rad produced by an accelerating point charge decreases as 1/r, while the static Coulomb field decreases as 1/r².  The static field decreases with distance much faster than the radiation field, and therefore the radiation field will dominate at large distance for accelerating charge distributions.  In addition, radiation fields are only produced by accelerating charges, (often the electrons), while static fields are produced by all charges (positive nuclei and negative electrons) and cancel each other out.

Far from the source of an electromagnetic wave, we often treat the EM wave as a plane wave.  A sinusoidal plane EM wave traveling in the x-direction is of the form

E(x,t) = E_maxsin(kx - ωt + φ),
B(x,t) = B_maxsin(kx - ωt + φ).

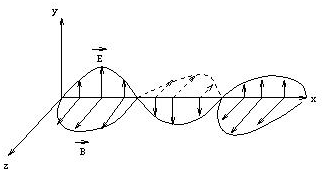If, for a wave traveling in the x-direction, E points in the y-direction, then B points in the z-direction.  Electromagnetic waves are transverse waves. 

The wave vector k points into the direction of propagation, and its magnitude k = 2π/λ, where λ is the wavelength of the wave.  The frequency f of the wave is f = ω/2π, ω is the angular frequency.  The speed of any sinusoidal wave is the product of its wavelength and frequency.

v = λf = ω/k.

The speed of any electromagnetic waves in free space is the speed of light c = 3*10⁸ m/s.
Electromagnetic waves in free space can have any wavelength λ or frequency f as long as λf = c.
Visible light is any electromagnetic wave with wavelength λ between approximately 400 nm and 750 nm.

Problem:

An electromagnetic wave in vacuum has an electric field amplitude of E_max = 220 V/m.  Calculate the amplitude B_max of the corresponding magnetic field.

Solution:

• Reasoning:
  The magnitude of the magnetic field is B = E/c.
• Details of the calculation:
  B_max = E_max/c = (220 N/C)/(3*10⁸ m/s) = (7.33*10^-7 N/Am) = 7.33*10^-7 T.

Problem:

The eye is most sensitive to light having a wavelength of 5.5*10^-7 m, which is in the green-yellow region of the electromagnetic spectrum.  What is the frequency of this light?

Solution:

• Reasoning:
  For all electromagnetic waves in free space λf = c.
• Details of the calculation:
  f = c/λ = (3*10⁸m/s)/(5.5*10^-7 m) = 5.455*10¹⁴ Hz.

Problem:

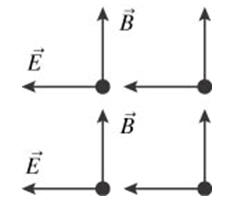A plane electromagnetic wave is propagating through space.  In some plane at some time t the fields are uniform and oriented as shown.  What is the direction of propagation of the plane wave?

Solution:

• Reasoning:
  The direction of propagation is the direction of E × B.  Using the right hand rule we find that the direction of propagation is into the page.

Electromagnetic waves can travel through transparent media, such as water and glass.  In a medium, they interact with the atoms or molecules, and due to this interaction have an apparent speed different from c.  When electromagnetic waves travel through a medium, the speed of the waves in the medium is v = c/n, where n is the index of refraction of the medium.  When an EM wave travels from one medium with index of refraction n₁ into another medium with a different index of refraction n₂, then its frequency remains the same, but its speed changes, and therefore it wavelength changes.  For air n is nearly equal to 1, for water n is 1.33, and for most glasses n is around 1.5.

Problem:

What is the apparent speed of light in water?

Solution:

• Reasoning:
  When electromagnetic waves travel through a medium, the speed of the waves in the medium is v = c/n, where n is the index of refraction of the medium.
• Details of the calculation:
  v = c/n = (3*10⁸ m/s)/1.33 = 2.26*10⁸ m/s.

Radio waves

Most radio waves are emitted by charges oscillating in antennas.  The direction of the acceleration of the charges is along the antenna.  A radio wave propagates from the antenna to the receiver along a straight-line path called the line of sight.  The direction of the electric field E of the electromagnetic radiation emitted by the antenna lies in a plane that contains the antenna and the line of sight to the receiver, and is perpendicular to the line of sight.  The wave is polarized, which means that E has a well defined direction.

The electric field is strongest and the intensity highest in the directions perpendicular to the antenna and goes to zero in the direction along the antenna.  You get very poor reception if you stand under the antenna.

To carry information, the electromagnetic wave must be modulated.  The information carried by a radio wave is sound.  The amplitude of an AM (amplitude modulated) radio wave represents the pressure variations, which make up the sound.  The frequency of FM (frequency modulated) radio waves can be shifted slightly from their nominal carrier frequency.  The amount of shift is proportional to the variations in the pressure, which make up the sound.