Please watch this short Youtube video clip.

When light propagates from air into glass or from glass in to air it may change its direction of travel.  Snell's law reveals the relationship between the directions of travel in the two media.
n₁sinθ₁ = n₂sinθ₂.
Consider light propagating in glass with index of refraction n₁ = 1.5 towards a glass-air boundary.  If the angle the light makes with the normal to the boundary in the glass is θ₁, then the angle it makes in the air is given by

sinθ₂ = (n₁/n₂)sinθ₁ = 1.5 sinθ₁.

If sinθ₁ > (1/1.5) = 2/3, or θ₁ > 41.8^o, then sinθ₂ is greater than 1 and there is no solution for θ₂.
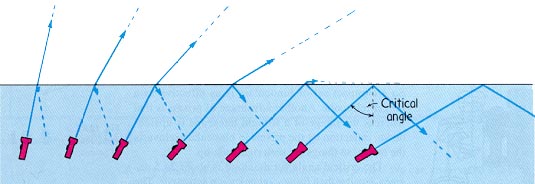
The angle θ_c for which sinθ_c = n₂/n₁ = 1 is called the critical angle.
For angles θ₁ greater than the critical angle there exists no solution for θ₂, and there is no refracted ray.
The incident light is totally reflected, obeying the law of reflection.  If n₂ = 1.5 and n₁ = 1 then the critical angle is θ_c = 41.8^o

Total internal reflection occurs only if light travels from a medium of high index of refraction to a medium of low index of refraction. 

Summary:  Let light travel from medium 1 into medium 2 and let n₁ > n₂. 
Then the critical angle θ_c is given by sinθ_c = n₂/n₁.
For angles greater than the critical angle the incident light is totally reflected, obeying the law of reflection.

Problem:

A light source is at the bottom of a pool of water (n = 1.33).  At what minimum angle of incidence will a ray be totally reflected at the surface?

Solution:

• Reasoning:
  The angle θ_c for which sinθ_c = n₂/n₁ = 1 is the critical angle.  For angles greater than the critical angle there is no refracted ray.
• Details of the calculation:
  For total internal reflection sinθ ≥ sinθ_c = 1/1.33, θ ≥ 48.7^o.

Embedded Question 2

Light enters through the side of a water-filled aquarium.  It is internally reflected at the critical angle θ_c at the top surface. What is θ_i in terms of θ_c and n_water?

Discuss this with your fellow students in the discussion forum!
Snell's law also applies to the ray entering the aquarium.

Prism reflectors

An ordinary glass mirror consists of a reflective metallic coating on the back of a sheet of glass. This is not the only way to make a mirror. Total internal reflection can be exploited to make a perfectly reflecting mirror using only glass, with no metal backing.  It is possible to use prisms of various shapes to reorient images.

Examples:

Right-Angle Prism

The prism is used like a mirror.  If the refractive index of the prism is large enough, we obtain Total Internal Reflection (TIR) and the prism acts like a mirror of 100% reflectance.
How large must the refractive index be?
We want the critical angle θ_c to be smaller than 45 degrees.  Since for a glass prism in air sinθ_c = 1/n, we need n > 1/sin(45^o) or n > √2 = 1.414.

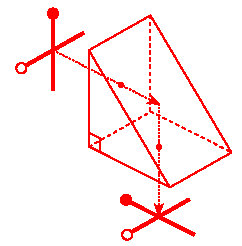
Dove Prism

This prism is used to "flip" an image without reorienting the optical axis.

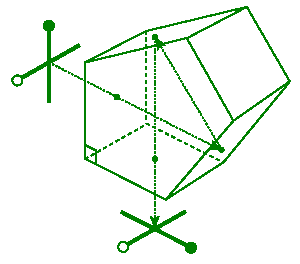
Penta Prism

Like the Right-Angle Prism, this prism reorients the optical axis by 90^o.  However, the Penta Prism does not flip the image.  Penta Prisms are used in 35-mm Single-Lens-Reflex (SLR) cameras to produce an upright image in the viewfinder.

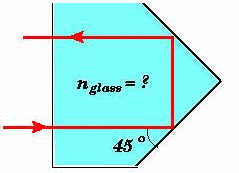Problem:

Assume you are using total internal reflection to make a corner reflector. If there is air outside and the incident angle is 45.0^o, what must be the minimum index of refraction of the material from which the reflector is made?

Solution:

• Reasoning:
  For total internal reflection we need sinθ ≥ sinθ_c = n₂/n₁.  Here n₂ = 1.  Therefore sinθ_c = 1/n.
• Details of the calculation:
  We need  sin(45^o) > 1/n, or  n > 1/sin(45^o) or n > √2 = 1.414.

Additional information:  The Physics Classroom: Refraction and the Ray Model of Light  Lessons 3