Optical properties of matter
Electromagnetic waves with wavelengths λ in the
range of ~400 nm to ~750 nm are called visible light. Maxwell's equations require that the speed v of any electromagnetic wave is
c =
1/(μ0ε0)½
= 3*108 m/s in free space.
Electromagnetic waves interact with the atoms and molecules of matter in various
ways.
Examples:
- Absorption
- Scattering
- Transmission
- Reflection
The details of the interactions can depend on wavelength and polarization.
Electromagnetic waves can travel
through transparent media, such as water and glass. In a medium, they
interact with the atoms or molecules, and due to this interaction have an
apparent speed different from c. When electromagnetic waves travel through
a transparent medium, the speed of the waves in the medium is v = c/n, where n is the
index of refraction of the medium. The index of refraction n is a property of the material.
For visible light in transparent materials n is, in general, greater
than 1, so that v is less than c in the material. In most transparent materials the index
of refraction depends slightly on the wavelength of the light, and in some
materials it depends on the polarization.
For light with frequency f traveling in a transparent medium we have v = λnf.
λn = λfree/n is wavelength of the light in the medium,
while λfree is its wavelength in free space.
When the index of
refraction changes, the wavelength of the light changes, while the frequency f
stays the same.
Why?
Refraction and reflection are due to light interacting with matter. Matter
is made up of charged particles. Light is electromagnetic radiation, i.e.
oscillating electric and magnetic fields. If the electric field oscillates
with frequency f, then it exerts an oscillating force on the charged particles,
and they start oscillating with the same frequency f. Oscillating charges
radiate themselves. They produce radiation with frequency f. The
radiation produced by the oscillating charges combines with the incident light
to produce the reflected and refracted beam through interference. But
whatever is produced has frequency f, since all the interfering radiation has
frequency f. However, the apparent speed of the refracted beam in the
medium changes, and therefore the wavelength in the medium has to change.
Problem:
What is the frequency of light that has a wavelength λn = 460 nm
in a liquid, if the index of refraction for this light is n = 1.2?
Solution:
- Reasoning:
λn = λfree/n is wavelength the light a the
medium with index of refraction n.
λfreef = c.
- Details of the calculation:
λfree = nλn = 460*1.2 nm = 552 nm.
f = c/λfree = (3*108 m/s)/(552*10-9 m)
= 5.43*1014 Hz.
The index of refraction n for light in air is nearly equal to 1. For
transparent materials the index of refraction listed in tables is
either an average index, or it is the index for one particular wavelength. In general, the
index of refraction n varies inversely with wavelength. It is greater for
shorter wavelengths. The table below gives the index of refraction for various
wavelengths of light in glass.
| Color |
Wavelength |
Index of refraction |
| blue |
434 nm |
1.528 |
| yellow |
550 nm |
1.517 |
| red |
700 nm |
1.510 |
Most materials are not transparent to visible light, but absorb or scatter
light. Even in transparent materials a small, (or not so small, depending
on the purity of the material), fraction of the light is absorbed or scattered.
We see light because it stimulates the cells in our eyes. Because our eyes are
able to distinguish between different wavelength of light we perceive color. If
the light reaching our eyes contains a broad mixture of wavelength, we interpret
it as white light.
Because light is an EM
wave, it exhibits several behaviors characteristic of waves such as
reflection, refraction and diffraction.
 A wave front is an
imaginary surface representing corresponding points of a wave that
vibrate in unison.
A wave front is an
imaginary surface representing corresponding points of a wave that
vibrate in unison.
The wave fronts of light emitted by a point
source are concentric spheres, centered on the source and expanding away
from the source at the speed of light.
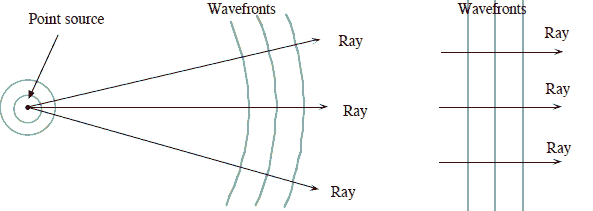 A light ray is an
imaginary directed line perpendicular to the wave front. At a
large distance from the source the curvature of the wave front can be
neglected and the wave front appears flat. The wave is then
approximated by a plane wave and the light rays are parallel.
A light ray is an
imaginary directed line perpendicular to the wave front. At a
large distance from the source the curvature of the wave front can be
neglected and the wave front appears flat. The wave is then
approximated by a plane wave and the light rays are parallel.
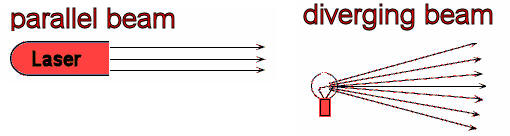 A beam of light has a non-zero width. We usually represent it by a few
rays.
A beam of light has a non-zero width. We usually represent it by a few
rays.
In a homogeneous, isotropic medium light travels in a straight line. When we
visually perceive the world around us, we implicitly assume that light follows a
straight-line path. But when light encounters a boundary between two media with
different indices of refraction, or when it travels through a non-homogeneous or
non-isotropic medium, its path may not be a straight line. If we can neglect
diffraction, because all obstacles in the path of the light wave have dimensions
much larger than the wavelength of the light, then we can analyze the propagation of light through different
media by analyzing the path of a light ray. This is called the
ray approximation of
geometrical optics.
Geometrical optics deals with the reflection and refraction of visible light, as
it moves through transparent materials with the dimensions of all obstacles much greater than the
wavelengths of light. We make the ray approximation.
 A wave front is an
imaginary surface representing corresponding points of a wave that
vibrate in unison.
A wave front is an
imaginary surface representing corresponding points of a wave that
vibrate in unison. A light ray is an
imaginary directed line perpendicular to the wave front. At a
large distance from the source the curvature of the wave front can be
neglected and the wave front appears flat. The wave is then
approximated by a plane wave and the light rays are parallel.
A light ray is an
imaginary directed line perpendicular to the wave front. At a
large distance from the source the curvature of the wave front can be
neglected and the wave front appears flat. The wave is then
approximated by a plane wave and the light rays are parallel. A beam of light has a non-zero width. We usually represent it by a few
rays.
A beam of light has a non-zero width. We usually represent it by a few
rays.