Fermat's principle:

Maxwell's equations can be used to derive the laws of reflection and refraction, which tell us how light waves behave at the boundary between two media with different indices of refraction.  In 1650, Fermat discovered a way to explain reflection and refraction as the consequence of one single principle.  It is called the principle of least time or Fermat's principle.

Assume we want light to get from point A to point B, subject to some boundary condition.  For example, we want the light to bounce off a mirror or to pass through a piece of glass on its way from A to B.  Fermat's principle states that of all the possible paths the light might take, that satisfy those boundary conditions, light takes the path which requires the least amount of time.

Embedded Question 1

Consider consider two people near the ocean.

• In situation A person 1 is on the beach and person 2 is in the water.  Person 1 must reach person 2 as quickly as possible.  (A lifeguard may have to get to a swimmer in distress.)  Which path should  person 1 take?  Make qualitative arguments. Assume that person 1 can run faster on the beach than swim in the ocean.
• In situation B person 1 and person 2 are both on the beach.  Person 1 must reach person 2 as quickly as possible while first getting some ocean water.  (Maybe a fire needs to be put out.)  Which path should  person 1 take?  Make qualitative arguments.

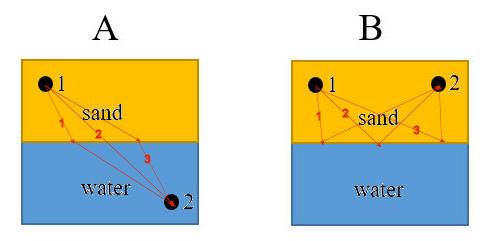
Discuss this with your fellow students in the discussion forum!
Consider the speed of of person 1 on the sand and in the water. 
Which path takes the least amount time in situation A and in situation B.

Light can travel faster in air than in water.  The qualitative arguments you make about the path that takes the least amount of time for the person near the sand-water interface in situations A and B also apply to the path of light light entering from air into water or reflecting from the air-water interface.  That is Fermat's principle.  Fermat's principle leads automatically to the principle of ray reversibility in geometrical optics.  It does not matter if you are going from A to B or B to A, the path that takes the least amount of time is the same.

Reflection

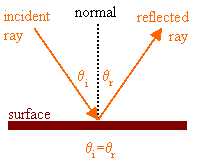Reflection is the abrupt change in the direction of propagation of a wave that strikes the boundary between two different media.  At least some part of the incoming wave remains in the same medium.  Assume the incoming light ray makes an angle θ_i with the normal of a plane tangent to the boundary.  Then the reflected ray makes an angle θ_r with this normal and lies in the same plane as the incident ray and the normal.

Law of reflection:  θ_i = θ_r.

Note:  In geometrical optics, angles are always measured with respect to the normal to the interface.

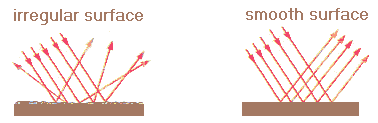Specular reflection occurs at smooth, plane boundaries.  Then the plane tangent to the boundary is the boundary itself.  Reflection at rough, irregular boundaries is diffuse reflection.  The smooth surface of a mirror reflects light specularly, while the rough surface of a wall reflects light diffusely.
The reflectivity of a surface material is the fraction of energy of the incoming wave that is reflected by the surface.  The reflectivity of a mirror is close to 1.

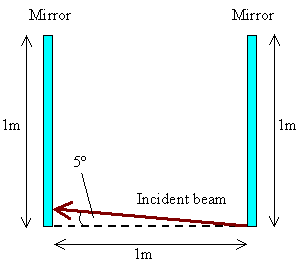Problem:

How many times will the incident beam shown in the figure to the right be reflected by each of the parallel mirrors?

Solution:

• Reasoning:
  After each path between the mirrors the beam gains a distance d in height.
• Details of the calculation:
  We have d/(1 m) = tan(5^o), d = tan(5^o) m = 8.75 cm. The beam must therefore pass 11 times between the mirrors to gain a height of 1 m, 6 times towards the left and 5 times towards the right.

Refraction

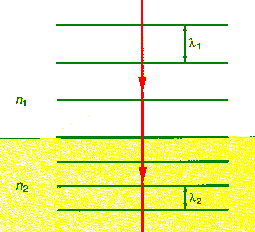Refraction is the change in direction of propagation of a wave when the wave passes from one medium into another and changes its speed.  Light waves are refracted when crossing the boundary from one transparent medium into another because the speed of light is different in different media.  Assume that light waves encounter the plane surface of a piece of glass after traveling initially through air as shown in the figure to the right.

What happens to the waves as they pass into the glass and continue to travel through the glass? 
The speed of light in glass or water is less than the speed of light in a vacuum or air.  The speed of light in a given substance is v = c/n, where n is the index of refraction of the substance.  Typical values for the index of refraction of glass are between 1.5 and 1.6, so the speed of light in glass is approximately two-thirds the speed of light in air. The distance between wave fronts will therefore be shorter in the glass than in air, since the waves travel a smaller distance per period T.
If f is the frequency of the wave and T = 1/f is the period, i.e. the time interval between successive crests passing a fixed point in space, then λ₁ = v₁T = cT/n₁ and λ₂ = v₂T = cT/n₂, or

λ₁/λ₂ = n₂/n₁.

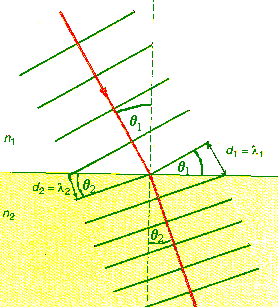Now consider wave fronts and their corresponding light rays approaching the surface at an angle.
We can see that the rays will bend as the wave passes from air to glass. The bending occurs because the wave fronts do not travel as far in one cycle in the glass as they do in air.  As the diagram shows, the wave front halfway into the glass travels a smaller distance in glass than it does in air, causing it to bend in the middle. Thus, the ray, which is perpendicular to the wave front, also bends.  The situation is like a marching band marching onto a muddy field at an angle to the edge of the field.  The rows bend as the speed of the marchers is reduced by the mud.

The amount of bending of the light depends on the angle of incidence and on the indices of refraction of glass and air, which determine the change in speed.  From the figure we can see that λ₁/λ₂ = sinθ₁/sinθ₂.
But λ₁/λ₂ = n₂/n₁.  Therefore n₂/n₁ = sinθ₁/sinθ₂, or n₁sinθ₁ = n₂sinθ₂.

This is Snell's law, or the law of refraction.
n₁sinθ₁ = n₂sinθ₂.

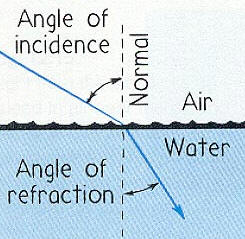
When light passes from one transparent medium to another, the rays bend toward the surface normal if the speed of light is smaller in the second medium than in the first.  The rays bend away from this normal if the speed of light in the second medium is greater than in the first.  The picture on the right shows a light wave incident on a slab of glass.
One part of the wave is reflected, and another part is refracted as it passes into the glass.  The rays bend towards the normal.  At the second interface from glass into air the light passing into the air is refracted again. The rays now bend away from the normal.

Parallel displacement:  When a light ray travels from air through a rectangular block of glass and the angle of incident is not equal to zero, then, upon reemerging from the glass, the light ray is displaced parallel to its original path.

Problem:

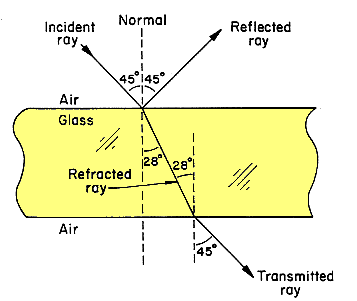The path of light in air incident on and transmitted through a glass plate is shown in the figure on the right.  The angle of the incident ray to the normal is 45^o and equals that of the reflected ray.  The transmitted ray is refracted at an angle of 28^o to the normal and exits the glass at an angle of 45^o to the normal, an angle equal to that of the incident ray.  What is the index of refraction of the glass?

Solution:

• Reasoning:
  We use Snell's law.
  n_isinθ_i = n_tsinθ_t
• Details of the calculation:
  As the ray enters from the air into the glass, we have n_i = 1, θ_i = 45^o, and θ_t = 28^o.  We therefore have n_t = n_isinθ/sinθ_t = sin45^o/sin28^o = 1.5.

Problem:

Assume a light signal travels in a straight line through a medium with index of refraction of n = 1.55, such as an optical fiber.  How long does it take the signal to travel 20 cm?

Solution:

• Reasoning:
  The speed of light in the medium is v = c/n.
• Details of the calculation:
  v = d/t.  t = d/v = (0.2 m)* 1.55/(3*10⁸ m/s) = 1.03*10^-9 s = 1.03 ns.

At a boundary between two transparent media, light is partially reflected and partially refracted.  The ratio of the reflected intensity to the incident intensity is called the reflectance R and the ratio of the transmitted intensity to the incident intensity is called the transmittance T.  Energy conservation requires that R + T = 1 (if there is no absorption).

Sunlight

Sunlight originates at the outer surface of the sun, in a region called the photosphere.  This region has a temperature of ~5800 ^oC.  The distribution of wavelengths in sunlight is determined by the temperature of the photosphere.  Not all sunlight is visible.  EM waves in the infrared and ultraviolet part of the EM spectrum are also produced in the photosphere.

Sunlight travels from the Sun to the Earth through empty space with the speed of light c.  When it enters the earth atmosphere it is refracted.  The index of refraction of air near sea level is only 1.0003, so the refraction is barely noticeable.  Air molecules, water molecules and dust also scatter some of the light (Rayleigh scattering).  These particles scatter shorter-wavelength light more efficiently that longer-wavelength light.  Scattering by tiny particles is always most efficient when the wavelength of the EM wave approximately matches the size of the tiny particle.  The dimensions of the molecules and dust particles are much smaller than the wavelengths of visible light, so blue light with the shortest wavelength provides the best match.  Blue light is scattered more than red light.  Most sunlight travels directly to our eyes, but the scattered light reaches us by a more complicated path from different directions.  We therefore see the brilliant yellow disk of the sun (direct light) and the fairly uniformly blue sky (scattered light).

As the sun rises or sets, light must travel a long distance through the Earth's atmosphere to reach our eyes.  Most of the blue light is scattered away during this passage through the atmosphere and the direct light from the sun appears red.  Extra dust and ash particles from pollution, forest fires, or volcanic eruptions enhance the Rayleigh scattering and are responsible for unusually red sunrises and sunsets.

Clouds and fog are composed of relatively large water droplets, larger than the wavelengths of visible light.  All wavelengths in the visible spectrum are scattered very efficiently by these large particles, so that very little direct sunlight reaches our eyes.  The scattered light, however, does not have any particular color, and clouds and fog appear white.

Problem:

Suppose there is a cloud made up of some unknown particles that absorb rather than scatter visible radiation.  What color would this cloud appear during the day?

Solution:

• Reasoning:
  The cloud would appear black, since no visible light would reach the observer from the direction of the cloud.

Additional information:

If you miss having regular lectures, consider this video lecture.