Optical instruments

To make the image of a small object on the retina as large as possible, you must move the object as close to your eye as accommodation allows. A magnifying glass enables you to enlarge the image on your retina even further. If you position the object less than or equal to one focal length f_mag away from the magnifying glass, and if the glass is positioned close to your eye, a magnified virtual image is formed (at least 25 cm from your eye). The eye forms a magnified real image of this enlarged virtual image on the retina.

We define the angular magnification m_α as the angle subtended by the virtual image (α_i) divided by the angle subtended by the object when viewed with the unaided eye (α_u).
m_α = α_i/α_uHere α_i and α_u are the angles made by the chief rays from the edge of the object with the optic axis in the case of the aided and unaided eye, respectively. The chief ray is the ray that passes through the center of the pupil.

A label such as "2X" or "10X" printed on a magnifying glass or an eyepiece belonging to a microscope or telescope indicates the angular magnification m_α when the object is positioned at the focal length f_mag of the magnifying glass, such that the virtual image is infinitely far away.
This is called the magnifying power MP.
MP = (25 cm)/f_mag.

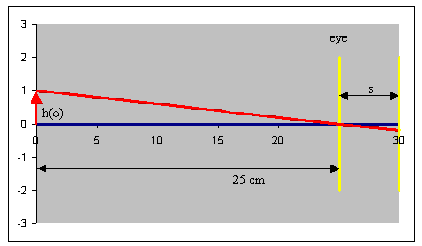Example:

In the figure on the right h(o) denote the height of the object and s the diameter of the eyeball.
If the object is a distance of 25 cm from the eye, then the tangent of the angle made by the chief ray from the top of the object is
tanθ_u= h(o)/25.
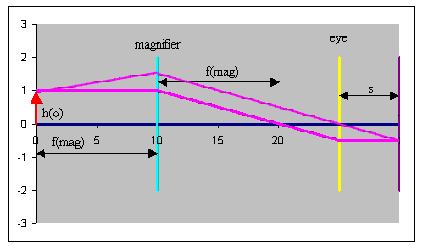viewing with a magnifying glass

With the object positioned at the focal length f_mag of the magnifying glass, the tangent of the angle made by the chief ray is
tanθ_i = h(o)/fmag.
(Rays coming from a point in the object focal plane of a lens emerge as parallel rays from the other side of the lens.
A ray entering parallel to the optic axis is deflected through the image focus.)

This yields in the small angle approximation
MP = θ_i/θ_u = 25 cm/f_mag.

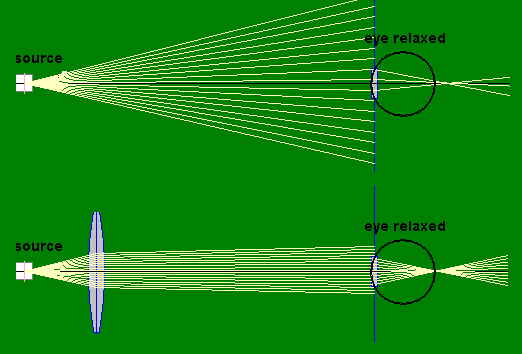
Placement of an object at the focal point of a magnifier or eyepiece is the ideal way to use these instruments, since the rays from the virtual image entering the eye are then parallel, and thus no accommodation is required to view the image on the retina.

A magnifying glass is an optical instrument consisting of a single lens and the eye. Other single lens optical instrument are a simple camera and a slide projector.

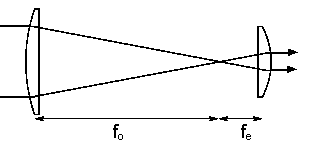
Keplerian telescope

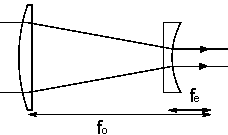
Galilean telescope

Telescopes

A basic refracting telescope is an optical instrument that has two optical elements, an objective and an eyepiece. We have two thin lenses in air. The objective is a large lens that collects light from a distant object and creates an image in the focal plane, which is a faithful representation of the object. The eyepiece is a sophisticated magnifying glass through which we view this image.

A Keplerian telescope has a converging lens eyepiece and a Galilean telescope has a diverging lens eyepiece. The distance between the image and the eyepiece is the sum of the focal lengths of the two lenses. (Remember that for a diverging lens the focal length is negative.) A telescope by itself is not an image forming system. The eye of the observer or the camera attached to the telescope forms the image.

We use a telescope to gather light and to increase the angle that a distant object subtends at the eye. The amount of light a telescope can gather increases with the square of the diameter of the objective. So a telescope with a 10 inch objective gathers 4 times as much light from a faint, distant source than a telescope with a 5 inch objective.

If the eye is relaxed for distant viewing, the telescope simply produces an angular magnification equal to the ratio of the focal length of the objective to the focal length of the eyepiece, M_θ = -f_o/f_e. An incident (approximately) parallel beam from a distant source point, which makes an angle θ with respect to the optical axis, emerges as a parallel beam which makes a larger angle θ' = -(f_o/f_e)θ with respect to the axis. If M_θ is negative, a viewer will see an inverted image.

(a)

(b)

A Keplerian (a) and a Galilean (b) telescope with the same angular magnification.

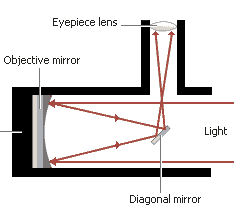
Newtonian Reflecting Telescope

Problem:

You want to build a Galilean telescope. You have two convex lenses and two concave lenses available. The larger lenses have focal lengths +80 cm and -80 cm respectively and the smaller lenses have focal lengths +20 cm and - 20 cm respectively. Which lenses should you use and how far apart should you place them

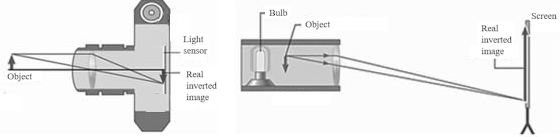
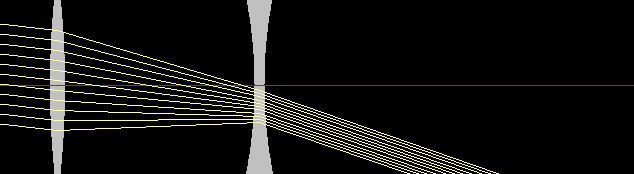
Microscopes

A compound microscope uses a simple combination of two converging lenses to produce a very effective magnifier. A sketch is shown below. The lens closest to the object is known as the objective, and the second lens is the eyepiece. The object is placed between f_o and 2f_o. An intermediate real image is formed by the objective lens near the object focal plane of the eyepiece. The tube length g is the distance between the secondary focal point of the objective and the primary focal point of the eyepiece. The intermediate image serves as the object for the eyepiece.

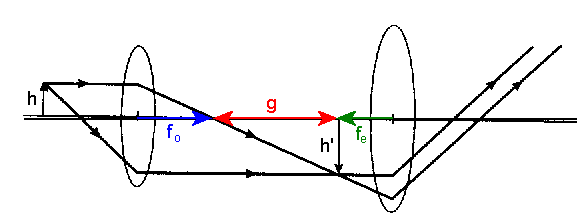
The total angular magnification or magnifying power of the microscope is given by MP = -(g/f_o)MP_eyepiece. A label such as "2X" or "10X" printed on the eyepiece belonging to a microscope or telescope indicates the angular magnification when the real image of the object is positioned at the focal length f_e of the eyepiece, such that the virtual image is infinitely far away. MP_eyepiece is given by MP_eyepiece = (25 cm)/f_e. The relaxed normal eye can then form an image on the retina. The focal lengths of both lenses should be extremely short to generate maximum angular magnification.

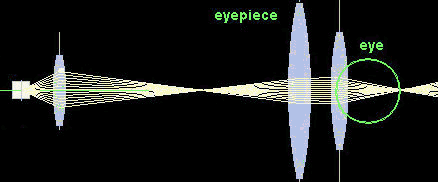
mcroscope 1

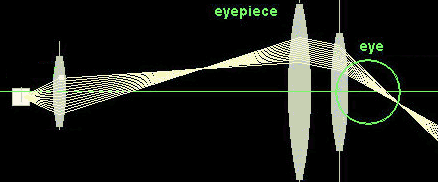
microscope 2

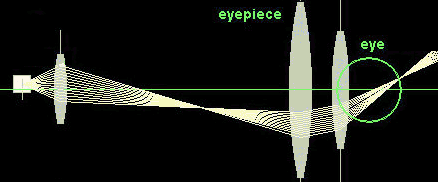
microscope 3

Illustration of the angular magnification of a microscope

The Magnifying Glass and Angular Magnification

Example:

Telescopes

Problem:

Microscopes