A single spherical interface between two transparent media can lead to image formation.  But viewing these images is not always possible.  Consider an air-glass interface.  When the object is on the air side, the image can only be viewed from inside the glass.  Giving the glass a finite thickness and adding a second spherical interface between glass and air will produce an image that can be viewed by someone in air.  A piece of glass of finite thickness with two spherical boundaries is a lens.  If the thickness of the lens is much smaller than the diameter of the lens, we call it a thin lens.

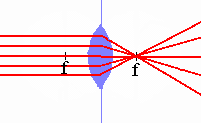
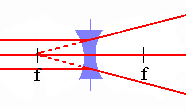
Thin lenses can be converging or diverging.  Converging lenses are thicker in the middle than near the edges, and diverging lenses are thicker near the edges than in the middle.  A thin lens has two focal points, located on the optical axis, a distance f from the center of the lens on either side of the lens.  Rays parallel to the optic axis passing through a thin converging lens come together at the focus f on the opposite side of the lens, and rays parallel to the optic axis passing through a diverging lens diverge as if they were leaving the focus on the incident side on a straight line path.

Converging lens
Diverging lens

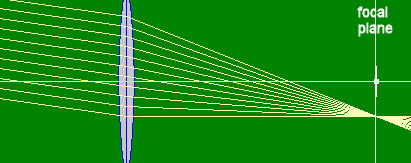
A plane through a focus perpendicular to the optic axis is called a focal plane.  Parallel rays converge in the focal plane or diverge from the focal plane, independent of the angle they make with the optic axis.

Real image


Virtual image

Thin lenses can form real and virtual images.

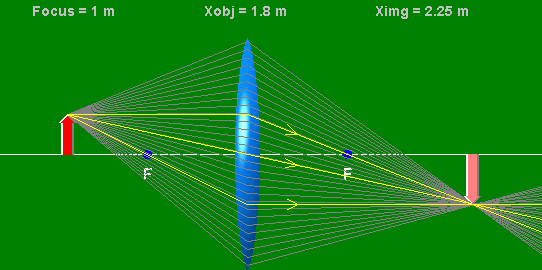
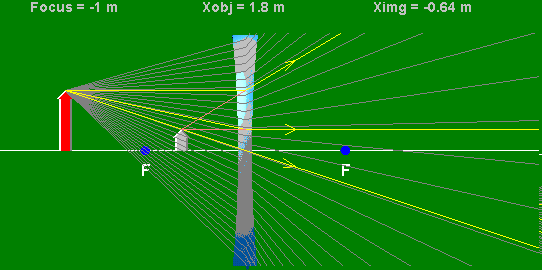
Let x_o denote the perpendicular distance of the object from the centerline of the lens and let x_o be positive.  Let x_i denote the perpendicular distance of the image from the centerline of the lens.  Then x_i can be found from the lens equation

1/x_o + 1/x_i = 1/f,

provided we use the following sign convention.

• x_o is positive for an object in front of the lens.
• x_i is positive if x_o and x_i are on the opposite sides of the lens.
• x_i is negative if x_o and x_i are on the same side of the lens.
• f is positive for a converging lens.
• f is negative for a diverging lens.
• The magnification is M = -x_i/x_o.
  If M is negative, the image is inverted.

We can find the position and size of the image geometrically.  Only two rays must be drawn.

• Draw the optical axis and the centerline of the lens.
• Mark the position of the foci.
• Draw the object in front of the lens.  Draw an incident ray parallel to the optical axis from a point on the object to the centerline of the lens, and a refracted ray from the centerline through f.
  • For a converging lens draw the refracted ray through the focus on the exit side, and for a diverging lens draw the refracted ray so that its extension passes through the focus on the incident side.
• Draw a second incident ray through f, and a refracted ray parallel to the optical axis.
  • The incident ray, or an extension of the incident ray, must pass through f. For a converging lens draw the incident ray or its extension through the focus on the incident side, and for a diverging lens draw the incident ray so that its extension passes through the focus on the exit side.
• The intersection of the two rays marks the position of the image.
• To check the accuracy of your drawing, draw a third ray through the center of the lens.  This ray is not bent.  It should pass through the intersection of the other rays that you have drawn.

Converging lenses form real inverted images if x_o> f and virtual upright images if x_o < f.

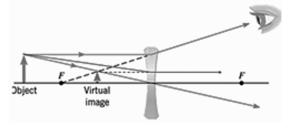
Diverging lenses only form virtual images.

Link:  Image formation ray tracing app
Drag the arrows and the lens while the app does the ray tracing.

The lens equation and the mirror equation are written as 1/x_o + 1/x_i = 1/f.
But the sign conventions for x_o, x_i, and f are different for lenses and mirrors.

• Mirrors reflect light, therefore real images are formed on the same side that the object is located on.  If x_i and f lie on that side, they are positive.
• Lenses transmit light, therefore real images are formed on the side of the lens opposite from the object.  If x_i and f lie on that side, they are positive.

Here are some things that always go together for a thin lens.

• Real image <--> inverted image <--> x_i is positive <--> M is negative
• Virtual image <--> upright image <--> x_i is negative <--> M is positive

Virtual image produced by converging lens <--> M > 1, (image is larger than object)

Virtual image produced by diverging lens <--> M < 1, (image is smaller than object)

The focal length of a thin lens is related to the radii of curvature of its two surfaces.
1/f = (n₂ - n₁)(1/R₁ - 1/R₂).

• R_i is positive, if x_o and the center curvature are on the opposite sides of the respective surface.
• R_i is negative, if x_o and the center curvature are on the same side of the respective surface.
• R₁ is the radius of the surface closest to x_o.

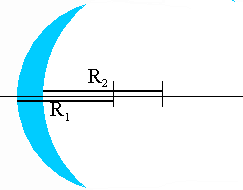Problem:

A contact lens is made of plastic with an index of refraction of 1.5.  The lens has an outer radius of curvature of 2 cm and an inner radius of curvature of 2.5 cm. What is the focal length of the lens?

Solution:

• Reasoning:
  The focal length of a thin lens is related to the radii of curvature of its two surfaces.
  1/f = (n₂ - n₁)(1/R₁ - 1/R₂).
• Details of the calculation:
  Both R₁ and R₂ are positive. Therefore
  1/f = (n₂ - n₁)(1/R₁ - 1/R₂) = (1.5 - 1)(½ - 1/2.5) = 0.05.  f = 20 cm.

The lens and mirror equations are valid for paraxial rays.  If all the light rays involved in image formation make small angles with the optic axis, so that sinθ ≈ tanθ ≈ θ, then near perfect images form at the locations predicted by these equations.  For off-axis or skew rays, the image of a point becomes blurry and we observe aberrations.

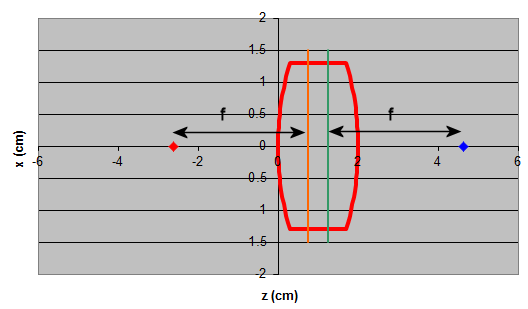Applying the lens equation to thin lenses, we can safely assume the light bends at the center of the lens, and neglect the thickness of the lens.  For thick lenses we have to be more careful.
One must calculate the location of principal planes, from which to measure distances to the object, the image, and the focal points.

Many optical instruments have more than one optical element.  A combination of mirrors and lenses can be analyzed by treating the image of the first element as the object of the second element, and so on.  If the image of the first element falls behind the second element we can still use the lens or mirror equation, but we then must use a negative object distance x_o.

Problem:

A thin lens has a focal length of 25 cm.  Locate the image when the object is placed
(a) 26 cm
(b) 24 cm
in front of the lens.  Describe the image in each case.

Solution:

• Reasoning:
  Use the lens equation.  1/x_o + 1/x_i = 1/f or  x_i = fx_o/(x_o - f).  M = -x_i/x_o.
• Details of the calculation:
  (a) x_i = 25*26/(26 - 25) = 650.  The image a real image 650 cm behind the lens. 
  Its magnification is M = -650/26 = -25.
  The image is inverted and enlarged.

  (b) x_i = 25*24/(24 - 25) = -600.
  The image a virtual image 600 cm in front of the lens.
  Its magnification is M = 600/24 = 25.
  The image is upright and enlarged.

Problem:

A magnifying glass is a converging lens of focal length 15 cm.  At what distance from a postage stamp should you hold this lens to get a magnification of +2?

Solution:

• Reasoning:
  Use the lens equation.  1/x_o + 1/x_i = 1/f.  M = -x_i/x_o.
• Details of the calculation:
  M = -x_i/x_o = 2,  x_i = -2x_o.
  1/x_o - 1/(2x_o) = 1/(2x_o) = 1/f = 1/15.
  x_o = 7.5 cm.

Problem:

A converging lens of focal length 4 cm is used as a magnifier.  If an object is placed 3 cm from the lens, what is the magnification?

Solution:

• Reasoning:
  Use the lens equation.  1/x_o + 1/x_i = 1/f.  M = -x_i/x_o.
• Details of the calculation:
  1/x_o + 1/x_i = 1/f,  1/3 + 1/x_i = 1/4, x_i = -12 cm.
  M = -x_i/x_o = 12/3 = 4.

Problem:

Assume two thin converging lenses with focal length f₁ and f₂, respectively, are very close to each other, so we can neglect the distance between them. They focus the light of a distant star at a focal point a distance f_eff from the lenses.  Find f_eff in terms of f₁ and f₂.

Solution:

• Reasoning:
  Use the lens equation.  1/x_o + 1/x_i = 1/f.
• Details of the calculation:
  x_o = infinite, so for the first lens 1/x_i = 1/f₁, x_i = f₁.  The image of the first lens becomes the object of the second lens.  It lies behind the second lens, and so the object distance for the second lens is -f₁.
  For the second lens we have -1/f₁ + 1/x_i = 1/f₂,   1/x_i = 1/f₁ + 1/f₂.
  But the image distance of the second lens is the focal length f_eff of the whole system.
  Therefore 1/f_eff = 1/f₁ + 1/f₂.

Embedded Question 1

Do you have a magnifying glass?  If not, do you have access to some prescription eyeglasses?  Make some observation with a single lens.

• Hold the lens about arms length away from your eyes and look at your bright computer screen with some text on it.  Move the lens closer to or farther away from the screen, keeping it about arms length away from your eyes.  What type of image do you see?  Does it appear to be in front or behind the lens?
  Remember:  Magnifying glasses are converging lenses with a relatively short focal length.  Eyeglass lenses may be converging or diverging, and they have relatively long focal lengths.
• Find a point source of light, such as a LED flashlight, keep it 2 -3 feet from the lens and shine its light through the lens. 
  Look at the images formed by reflection off the front and back side of the lens by looking at the lens from the direction of the light source.  The surfaces of the lens act like mirrors.
  
  What type of images do you see?  Do they appear to be in front or behind the lens?  If you are using eyeglasses turn them around, so that you can observe reflections off convex and concave surfaces.

Discuss your observations with your fellow students in the discussion forum!

Additional information:  The Physics Classroom: Refraction and the Ray Model of Light  Lesson 5