Michelson Interferometer

The Michelson interferometer is an optical instrument of high precision and versatility.  It is generally used in investigations that involve small changes in optical path length, from a fraction of a wavelength to a few wavelengths.  With the Michelson interferometer, one can produce circular and straight-line fringes of both monochromatic light and white light.  One can use these fringes to make an accurate comparison of wavelengths, measure the refractive index of gases and transparent solids, and determine small changes in length quite precisely.  The Michelson interferometer was introduced by Albert Michelson in 1881.  It has been used to

• provide experimental evidence for special relativity,
• discover the hyperfine structure in the energy levels of atoms,
• measure tidal effects of the moon on the earth,
• enable the use of wavelength of light as the international standard for the meter.

The Michelson interferometer operates on the principle of division of amplitude rather than on division of wave front (slits).  According to this principle, the incident beam of light falls on a beam splitter, which reflects roughly half of the intensity of the wave front in one direction and transmits the other half of the intensity of the wave front in another direction.  The two beams, which travel different optical paths, are subsequently recombined in a common region where interference occurs and fringes are formed. The character of the fringes is directly related to the difference in the optical path lengths for the two beams.  It is therefore related to whatever causes a difference in the optical path lengths.

In its most common arrangement, a Michelson interferometer is illuminated by an extended source S and consists of a 50% beam-splitter BS and two mirrors M₁ and M₂. The interference pattern is observed on a screen that is either very far from BS, or a lens is placed one focal length in front of the screen. Rotation or translation of one or both mirrors changes the interference pattern.

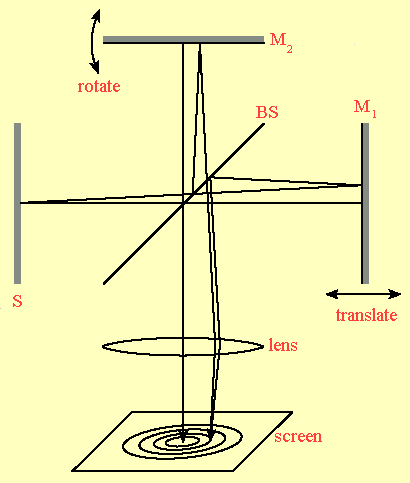
Interference in a Michelson interferometer can be understood in terms of thin-film interference.  Imagine that the arms of the interferometer are rotated, such that there is a single optical axis, as shown in the drawing below.

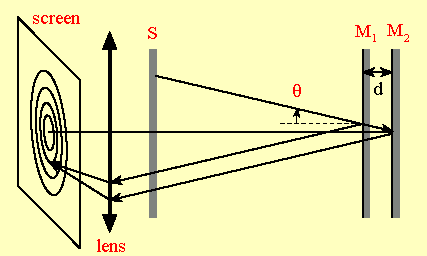
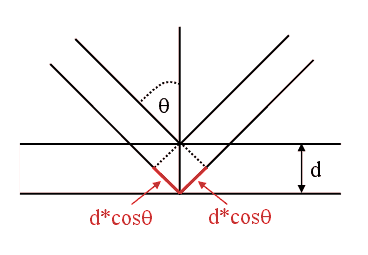
Then reflection from the mirrors M₁ and M₂ is analogous to reflection from two surfaces of an air gap of thickness d.  Since the phase shift upon reflection is the same for both mirrors, we find

2d cosθ = mλ

for constructive interference.

If the two mirrors are precisely aligned such that their planes are exactly perpendicular to one another, thus ensuring that path differences over different regions of the mirrors are constant, the fringe pattern will consist of a series of concentric rings.  Each ring will correspond to a different angle of view, measured from the normal to the mirror M₁.  These fringes are called fringes of equal inclination. They are analogous to fringes of equal inclination that we observe when we shine light from an extended source on a thin film.  When the mirror M₁ is moved so as to approach the condition for zero path difference, the fringe pattern appears to collapse, with all fringes moving towards the center, and disappear.

Link:  Michelson Interferometer
Link:  Neil deGrasse Tyson explains the Michelson-Morley experiment