Consider an object moving in the gravitational field of the Earth. Its
acceleration is a = -GMEr/r3, where
r is the position
vector directed from the center of the Earth to the object. Choose the origin
of your coordinate system at the center of the Earth and assume the object is
moving in the x-y plane. Then the Cartesian components of the object's
acceleration are
ax = -GMEx/(x2+y2)3/2,
ay = -GMEy/(x2+y2)3/2.
Write a spreadsheet or computer program to find the position of the object as
a function of time. Assume that the initial position of the object is at x
= 0, y = 2RE, where RE is the radius of the Earth, and give the object an
initial velocity of 5 km/s in the x direction. The time increment should be
made as small as practical. Try 5 s.
Your spreadsheet should look similar to the one shown below. You can
use the attached spreadsheet as a starting point.
| |
A |
B |
C |
D |
E |
F |
G |
H |
| 1 |
time |
x |
y |
ax |
ay |
vx |
vy |
r |
| 2 |
0 |
0 |
1.27E+07 |
0 |
-2.45842 |
5.60E+03 |
0 |
12740000 |
| 3 |
5 |
2.80E+04 |
1.27E+07 |
-0.005403 |
-2.45841 |
5599.99 |
-12.29 |
12740000 |
| 4 |
10 |
5.60E+04 |
1.27E+07 |
-0.010806 |
-2.45839 |
5599.95 |
-24.58 |
12740000 |
- Use SI units consistently.
- For ax and ay use the formulas given above, and
let them refer to the x and y values in the same row.
- Use the given initial conditions for x, y, vx, and vy
in the first row. Let r = SQRT(x2+y2).
- Use x = x0 + vxΔt and y = y0 + vyΔt
with x0 , y0, vx, and vy from
the previous row to find x and y in later rows. (You are using the
Euler method to solve a differential equation numerically.)
- For example, in the spreadsheet shown above, type =B2+F2*(A3-A2)
into cell B3.
- For smaller numerical errors, use x = x0 + vxΔt
+ ½axΔt2 and y = y0 + vyΔt
+ ½ayΔt2. For example, type
=B2+F2*(A3-A2)+0.5*D2*(A3-A2)^2 into cell B3.
- Use vx = vxo + axΔt and vy =
vy0 + ayΔt with vxo , vyo, ax,
and ay from the previous row to find vx and vy
in later rows.
- For example, in the spreadsheet shown above, type =F2+D2*(A3-A2)
into cell F3.
- For smaller numerical errors, use vx = vxo+axΔt+½(Δax/Δt)Δt2
and vy = vy0 + ayΔt + ½(Δay/Δt)Δt2.
For example, type =F2+D2*(A3-A2)+0.5*(D3-D2)*(A3-A2) into cell F3.
- If you use 5 s time intervals you need to copy your formulas down
approximately 3000 rows for one complete revolution.
- Produce a scatter plot of y versus x similar to the plot shown below.
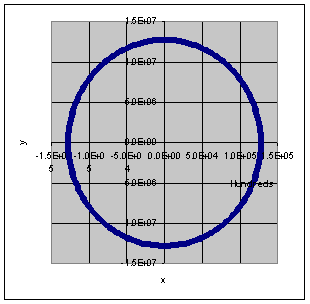
- Vary the magnitude of the initial velocity until a circular orbit is
found.
- If r becomes smaller than the radius of the earth, the objects hits
the earth.
- Add three columns to your spreadsheet to calculate the kinetic energy,
potential energy and total energy as a function of time. (Set the mass of
orbiting the object equal to 1 kg.) How do they vary with time? (Note the
potential energy and the total energy will be negative.)
To earn extra credit add your name and e-mail address to your spreadsheet and
submit your spreadsheet for an initial speed of 5 km/s and for the initial speed
corresponding to your most circular orbit. In a few sentence describe how
the kinetic, potential and total energy vary with time in those two cases.
What is the initial velocity for the most circular orbit?
Save your Excel spreadsheet (your name_ex8.xlsx), go to Canvas, Assignments,
Extra Credit 8, and submit your spreadsheet.
