Work and Energy

Energy conservation for an isolated system is a fundamental principle of physics.  Energy for an isolated system is always conserved.  It may change forms, but the total amount of energy in an isolated system is constant.  Energy can, however, be converted from one form to another form.  Work is the conversion of one form of energy into another.  Energy comes in different forms, kinetic energy, potential energy, chemical energy, thermal energy, etc.  If an object has energy, it has the potential to do work. 

There are several forms of potential energy.  Kinetic and potential energy are called mechanical energy or ordered energy.  Thermal energy is disordered energy.  Friction converts mechanical energy into disordered energy.
When no disordered energy is produced, then mechanical energy is conserved.

In this lab we will use an on-line simulation from the University of Colorado PhET group to track mechanical energy in a skate park, and you will analyze two video clips to track the mechanical energy of a bouncing ball.

Open a Microsoft Word document to keep a log of your experimental procedures, results and conclusions.  This log will form the basis of your lab report.  You should address all items in blue.

Part 1

Use an on-line simulation from the University of Colorado PhET group to track mechanical energy in a skate park.
Link to the simulation: https://phet.colorado.edu/en/simulations/energy-skate-park-basics

• You can build tracks, ramps and jumps and view graphs of kinetic energy, potential energy and friction as the skater moves.

(a)  Click the Playground image.  Explore the interface!
Note:

• You can Pause the simulation and then put the Skater anywhere.  Restart  Skater returns the Skater to this spot and you can rerun the scenario.
• You can fix the skater to the track or let him loose contact with the track.

(b)  Design your own frictionless track.

• Design a track that is fun, challenging and relatively safe.
• Use the Energy Graphs to track the Skater's mechanical energy.  Decide which graphs or charts best help you understand what makes your track successful.
• Explain why your track is successful in terms of conservation of mechanical energy.  Refer to Charts or Graphs to help explain your reasoning.
• Using conservation of mechanical energy, explain what things need to be considered when designing any successful track.

(c)  Add friction to your track.

• Explain what changes in the simulation when you add friction.  How does the energy distribution change?

Part 2

Measure the spring constant of a spring.
One end of a spring is attached to a rigid support.
Different weights are hung on the other end, and the spring stretches to different lengths.

Procedure:

• In the pictures below measure the position of the free end of the spring as a function of the applied force.  Always measure the position of the same physical point. 
• Measure the position in units of meter and the force in units of Newton.  Enter your data into a spreadsheet.  Your first rows should look similar to this.

• Use the spreadsheet to plot the applied force versus the position of the free end of the spring.
  Scatter plot:  Vertical axis: force,  Horizontal axis: position.
• Use the spreadsheet's trendline to determine slope of the straight line that best fits the data.  Format the trendline label to show a number with at least 2 decimal places.
  Since F_applied = kx,  ∆F_applied = k∆x, and the slope of the straight line will be equal to the spring constant k.
  What is the value of the spring constant k (magnitude and units)?
  What is the equilibrium position x_equ of the free end of the spring in units of cm, i.e. in your graph, what is x (in m) when y = 0?

Add two columns to your spreadsheet.  For each position, enter the elastic potential energy stored in the spring, ½k(x - x_equ)², and the work done by gravity, mg(x - x_equ) = F(x - x_equ).

Gravity does work, converting gravitational potential energy into other forms. 

• Is the gravitational potential energy lost equal to the elastic potential energy stored in the spring?
  If not, approximately how much of the work done by gravity is stored in the spring, and what do you think happened to the rest of it?
• Add a plot of  ½k(x - x_equ)² to your graph and paste your graph into your log.

Part 3: 

The coefficient of restitution

Analyze two video clips.  The clips shows bouncing balls.   By measuring the maximum height a ball reaches after each bounce, you can determine the coefficient of restitution of the ball.   For a review, click here.

Each ball starts with no kinetic energy and potential energy U = mgh₁.  As it contacts the floor, it has no potential energy but kinetic energy K₁ = U₁, or ½mv₁² = mgh₁.  After the bounce, just as it breaks contact with the floor it has kinetic energy K₂ = ½mv₂² and no potential energy.  When it reaches its maximum height after the bounce, it has no kinetic energy, but potential energy U₂ = K₂, or mgh₂ = ½mv₂².  We therefore have

K₂/K₁ = U₂/U₁, or v₂²/v₁² = h₂/h₁.

In the video clips you must find the highest point above the floor that the ball reaches after two successive bounces.  You can do this by choosing  to track the y-coordinate of the ball.  Calibrate Y by clicking at the bottom and the top of the meter stick, and entering 1 m for the distance between calibration points.  After you finish taking data, import your data into Excel and construct a graph of position versus time.  You can read the maximum heights right off this graph by moving your cursor over the highest points.  For example in the graph below the height after the first bounce is 1.022 m, after the second bounce it is 0.956 m, and after the third bounce it is 0.899 m.

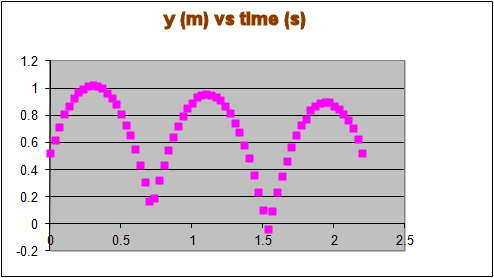
To find the ratio of the speeds after successive bounces use  v₂²/v₁² = h₂/h₁.  The ratio v₂/v₁ is the coefficient of restitution.   (Since you have 3 bounces, you can find the ration for bounce 2 and 1 and the ratio for bounce 3 and 2.  You can average, to get a more accurate result.)

To play each video clip or to step through it frame-by-frame click the "Begin" button.  The "Video Analysis" web page will open.  Choose the restitution_1.mp4 video clip to determine the coefficient of restitution of a super ball and the restitution_2.mp4 video clip to determine the coefficient of restitution of a golf ball.

• Paste your position versus time graphs into your log.
• Determine the coefficient of restitution for the super ball and the golf ball.  Describe your procedure.
• What value did you obtain for the coefficient of restitution of the super ball?
• What value did you obtain for the coefficient of restitution of the golf ball?
• What is the significance of these values?  What does the coefficient of restitution tell you about energy? 
• Which ball is the "livelier" ball?

Convert your log into a lab report.

Name:
E-mail address:

Laboratory 6 Report

• In one or two sentences state the goal of this lab.
• Insert your log with the requested graphs and the answers to the questions in blue font.

Save your Word document (your name_lab6.docx), go to Canvas, Assignments, Lab 6, and submit your document.