A mass on a spring and a pendulum

In this lab you will explore the motion of a mass attached to a spring hanging vertically from a fixed support and the motion of a simple pendulum.

Open a Microsoft Word document to keep a log of your procedures and your results.  This log will form the basis of lab report.  Address the points highlighted in blue.  Answer all questions.

Experiment

A spring has an equilibrium length L.  When a spring is compressed, then a force with magnitude proportional to the decrease in its length from its equilibrium length is pushing each end away from the other.  When a spring is stretched, then a force with magnitude proportional to the increase in its length from its equilibrium length is pulling each end towards the other.

If one end of a spring is fixed to a support and an object is attached to the other end, then the force exerted by the spring on the object has a magnitude proportional to the displacement ΔL of the free end from its equilibrium position.  The direction of the force is always opposite to the direction of the displacement.  If the x-axis of a coordinate system is chosen parallel to the spring and the equilibrium position of the free end of the spring is at x = 0, then the displacement ΔL is equal to x, and the force is F = -kx.  The proportional constant k is called the spring constant.  It is a measure of the spring's stiffness.

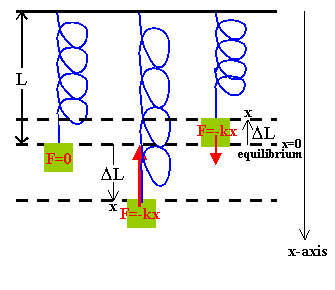
If an object attached to the free end of the spring is displaced along the x-axis (in the positive x-direction) and then released, the force exerted by the spring on the object will accelerate it towards the equilibrium position (in the negative x-direction).  When it reaches the equilibrium position it will have its maximum speed.  As it passes through the equilibrium position, the force the spring exerts on the object changes direction.  The object now decelerates, until its speed is zero and it displacement is maximum in the negative x-direction.  The acceleration is in the positive x-direction and the object again accelerates towards the equilibrium position.  The object oscillates about the equilibrium position.

• The position of the object as a function of time t is x = x_maxcos(2πft + φ).
  x_max is the amplitude of the oscillations and f is the frequency.
  φ is the phase of the oscillations.  
  The period T of the oscillations is T = 1/f.
• The velocity of the object as a function of time t is v = -v_maxsin(2πft + φ).
  v_max is the maximum speed of the object as it passes the equilibrium position.
• The acceleration of the object as a function of time t is a = -a_maxcos(2πft + φ).
  a_max is the magnitude of the acceleration of the object at maximum displacement.
  The force acting on the object is F = ma.

You will measure the period of the oscillations of different masses attached to the same spring.  For a mass on a spring we expect

ω = √(k/m),  T = 2π√(m/k).

To find the spring constant k you will plot T² versus m.  The slope of the best fitting straight line equals 4π²/k.

Procedure:

You will analyze 4 video clips,  spring_x.mp4, x = 1 - 4.  To play a video clip or to step through it frame-by-frame click the "Begin" button.  The "Video Analysis" web page will open.

Begin

Analyze each of the clips to find the period of oscillation.  Track the point where the mass attaches to the spring. (See Lab 9, hints.)
The weight of the object attached to the spring is given.  Find its mass.  Construct a spreadsheet as shown below.

• Construct a plot of T² versus m.
• Use the spreadsheet's regression function to find the slope of the best fitting straight line to this plot and the uncertainty in the slope.
• Find the spring constant k and the uncertainty in this value, Δk.  Use Δk/k = Δ(slope)/(slope).

Paste  your table and plot of T² versus mass and your value for the slope of the best fitting straight line into your log.
What value did you find for k and what is the uncertainty in k?

Exercise

In this exercise you will explore "The pendulum Lab" simulations.
Link to the simulation:  https://phet.colorado.edu/en/simulations/pendulum-lab
Click the "Lab" window.

The interface

• If you want to do an experiment, "Pause" the simulation, set up your experiment, then start it.
• If you want to compare what happens when you change a variable, such as the length, click the icon with the two masses, set up your experiment, then start it.
• The "Period Timer" operates as a triggered mechanism, which starts when the pendulum crosses the vertical dotted line.  The period will be displayed after one cycle.
• The timer, the stop watch, and the ruler can be dragged.
• The initial angle is marked by a tick mark with the color of the pendulum mass.
• As you move the pendulum, the angles are constrained to be exactly integer number of degrees.

Make the following measurements and answer the questions below

Let the length of the pendulum be 0.8 m and the mass be 0.5 kg.  Choose no friction.  The formula for the period of a pendulum derived in the notes is T = (2π) (L/g)^1/2 for small oscillations.

• Calculate the expected period of the pendulum.  What is the expected period?
• Start the pendulum on Earth with an amplitude of 10 degrees.  Measure the period and record it.  Is the measured period equal to the calculated period?
• Start the pendulum on Earth with an amplitude of 50 degrees.  Measure the period and record it.  Is the measured period equal to the calculated period?
  Does the period of a simple pendulum noticeably depends on the amplitude for large amplitudes?
• Repeat everything with the same pendulum length but a 1.5 kg mass.  For the same amplitude and the same pendulum length, does the  period depend on the mass?
• Introduce damping by turning on a medium amount of friction and monitor the period, starting the pendulum at 50 degrees.  Measure the period several times before the motion damps out.  Does the damped pendulum have a constant period?
• Compare the periods of the same undamped pendulum on Earth, Moon, Jupiter, Planet X, and in a zero g environment.  Always start the pendulum at 10 degrees.  In a zero g environment does the pendulum  execute oscillatory motion?
• Devise a way to determine g_X, the gravitational acceleration near the surface of planet X.  What is g_X in units of m/s²?

Convert your log into a lab report.

Name:
E-mail address:

Laboratory 9 Report

• In one or two sentences state the goal of this lab.
• Insert your log with the requested table, graphs, and the answers to the questions in blue font.

Save your Word document (your name_lab9.docx), go to Canvas, Assignments, Lab 9, and submit your document.