We measure point in time t by using a clock. The SI unit of time is the second. The clock reading in seconds depends on the choice of origin. Clocks in different time zones have different readings and the reading of a stop watch depends on when it was started. A time interval ∆t = tlater - tearlier is defined as the difference between a later time and an earlier time. It is always a non-negative number (positive or zero). A interval ∆t is a scalar, a number with units.
When an object moves through space, its position changes. Assume that at a time t1 it is at a position P1 and at a later time t2 it is at position P2. The displacement vector is d = P2 - P1. In the time interval ∆t = t2 - t1 the object has been displaced by d. Its average velocity in that time interval ∆t is defined as <v> = d/∆t. The displacement d is a vector, the time interval ∆t is a scalar. Dividing a vector by a scalar yields another vector. The average velocity <v> is a vector. The average speed is the distance traveled in the time interval ∆t divided by ∆t. The distance is a scalar, i.e. a number with units. Dividing the distance by ∆t yields another number with units. The average speed is therefore a scalar.
In a time interval of 5 minutes, a runner runs once around a one-mile track. What is his average velocity? What is his average speed?
Solution:
A sprinter runs north in a straight line and covers a distance of 100 m in 12 s. What is her average velocity? What is her average speed?
Solution:
Summary
The average speed is the distance covered divided by
the time it took to cover this distance. If a
person walks 1 km west, then turns around and walks 1 km east, the distance this
person covers is 2 km. If it takes 20 minutes to cover this distance then the
average speed is 2 km/ 20 minutes = 2000 m/ (20*60 s) = 1.67 m/s.
The average velocity is a vector. It is the
displacement vector pointing from the initial position to the final position,
divided by the time. In the above example the
initial and the final position are the same. The displacement vector is zero.
So the average velocity is zero.
Link: Speed and velocity (Please explore!)
Since the magnitude and direction of the displacement vector depend on the reference frame in which the coordinate system is anchored and at rest, the velocity of and object depends on the reference frame with respect to which it is measured.
A car has moved forward a distance of 6 m, while a child has moved forward from the back seat to the front seat a distance of 1 m in a time interval of 2 s. Find the average velocity of the child relative to the car and relative to the road.
Solution:
Note: The velocity of an object depends on the reference frame, it is
not a quantity all observers agree on. An object can be at rest in one
reference frame, and having non-zero velocity in another reference frame.
When a parent tells a child to sit still in a moving car, they mean to sit still
with respect to the car, not with respect to the road.
Stopped, you wait for the traffic light to change from red to green, when suddenly you have the feeling that you are moving, even though you are pressing on the brake pedal. But then you notice that the big truck or bus in the lane next to you is the vehicle that is actually moving with respect to the ground. To conclude that we are moving with respect to the ground, we mostly rely on visual clues. When we see our surroundings moving we conclude that we are moving. Usually we can quickly establish the true situation, as we subconsciously realize that there is a discrepancy and quickly obtain additional information from our surroundings.
The simulation below explores relative motion. The view is always that of a driver in a car, or someone moving with the same velocity as the driver looking straight into the picture. You can choose three different situations and zoom and rotate the view, Please click on the image!
Often the average velocity is not a very useful quantity. We want to know the velocity of an object at an instant of time. We want to know the instantaneous velocity. The more we reduce the time interval between two successive position measurements, the closer is the average velocity measured for that time interval to the instantaneous velocity. We define the instantaneous velocity as
v = lim∆t-->0∆r/∆t = dr/dt,
where ∆r is the displacement in the time interval ∆t. The instantaneous speed is the magnitude of the instantaneous velocity. From now on we will assume that the words velocity and speed stand for instantaneous velocity and instantaneous speed unless explicitly stated otherwise.
A short review of derivatives (Please review if you are taking calculus concurrently.)
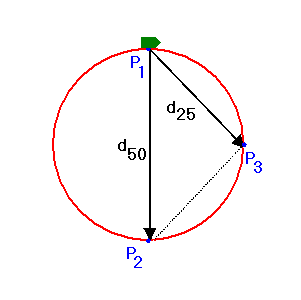 Assume a car is moving on a circular track with a 1000 m circumference. It moves
with constant speed v = 10 m/s. At t = 0 it is at point P1, moving east.
Assume a car is moving on a circular track with a 1000 m circumference. It moves
with constant speed v = 10 m/s. At t = 0 it is at point P1, moving east.
At t = 100 s, it is again at point P1, moving east. Its velocity averaged over
100 s is 0.
At t = 50 s, the car is at point P2, moving west. Its displacement vector for
the first 50 seconds is d50 = 1000 m/π south = 318 m south. Its velocity
averaged over the first 50 seconds is v = d50/(50 s) south = 6.36 m/s south.
At t = 25 s the car is at point P3. Its displacement vector for the first 25 s
is d25 = 318 m/√2 southeast = 225 m southeast. Its velocity averaged over the
first 25 s is v = d25/(25 s) southeast = 9 m/s southeast.
The shorter the time interval between successive position measurements, the
closer is the average velocity to the instantaneous velocity, which is 10 m/s
tangential to the circle.
Link: Average vs. Instantaneous Speed
Can the magnitude of the average velocity be larger than the average speed?
Solution:
Since the magnitude and direction of the displacement vector depend on the reference frame in which the coordinate system is anchored and at rest, the velocity of and object depends on the reference frame with respect to which it is measured.
Whenever the velocity of an object is changing, then the object is
accelerating. Assume that at a time t1 the object has velocity
v1,
and at a later time t2 it has velocity v2. The change in
velocity is ∆v = v2 -
v1
in the time interval ∆t = t2 - t1.
The object's average acceleration in that time interval
∆t is defined as <a> = ∆v/∆t.
The average acceleration
<a> is a vector.
It is the velocity vector at the final time, minus the velocity vector at
the initial time, divided by the time interval.
We define the instantaneous acceleration as
a = lim∆t-->0∆v/∆t = dv/dt,
where ∆v is the change in velocity in the time interval ∆t. From now on we will assume that the word acceleration stand for instantaneous acceleration, unless explicitly stated otherwise.
Link: Acceleration
Note: Whenever your velocity is CHANGING, you are accelerating. You are accelerating when you CHANGE your speed, CHANGE your direction of travel, or both. The keyword is CHANGE.
If your velocity is NOT changing, then, no matter haw fast you are moving, you are NOT accelerating.
constant velocity <--> zero acceleration
You are driving at a constant speed of 20 miles/h around a city block, checking out the neighborhood. Are you accelerating?
Solution:
You are traveling east at 30 miles per hour. You see a ball rolling onto the road and you break hard, because you are afraid that a child will come running after the ball. You come to a stop in 0.8 seconds. What is the direction of your average velocity in this short time interval? What is your average acceleration?
Solution:
Links: Acceleration, Uniform circular Motion
Note: Acceleration is absolute. The acceleration of an object does not depend on the reference frame, it is a quantity all observers agree on. Even without outside references you can determine if you are accelerating.
An elevator ride: You momentarily feel heavier when the elevator accelerates upward and lighter when it accelerates downward.
As your turn your car suddenly to the left, loose objects on the dashboard start sliding to the right. Are these objects accelerating to the right?
Discuss this with your fellow students in the discussion forum!