Free Fall
Systematic experiments on freely falling objects were carried out by
Galileo Galilei
(1564-1642). Near the surface of the earth all freely falling objects
accelerate at approximately the same rate. This acceleration is denoted by
g. Its direction is downwards, towards the center of the earth. Freely falling objects move with constant acceleration
g = 9.8 m/s2
downward.
Problem:
You drop a ball from a window on an upper floor of a building. It
strikes the ground with speed v. You now repeat the drop, but you have a
friend down on the street, who throws another ball upward with the same
speed v. Your friend throws the ball upward at the same time you drop yours
from the window. At some location the balls pass each other. Is this
location at the halfway point between the window and the ground, above this
point, or below this point?
Solution:
- Reasoning:
Both balls are accelerating. The ball thrown upward
will reach the window at the same time the dropped ball reaches the ground.
The speed of the dropped ball increases linearly with time. The ball
moves with the slowest speed near the window and with the fastest speed near
the point it hits the ground. In half the time it takes to reach the
ground it covers less than half the distance and is still above the midpoint
between window and ground. The speed of the ball thrown upwards
decreases linearly with time. It moves fastest near the ground and
slowest near the window. In half the time it takes to reach the
window, it is already above the midway point. The two balls therefore
meet above the midway point.
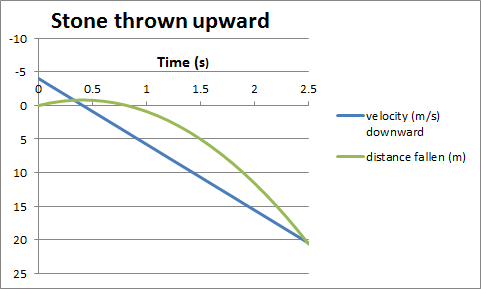
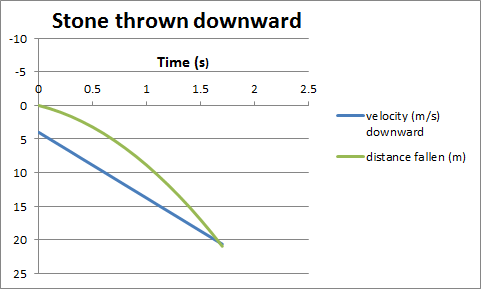
We can also work with our
kinematic equations.
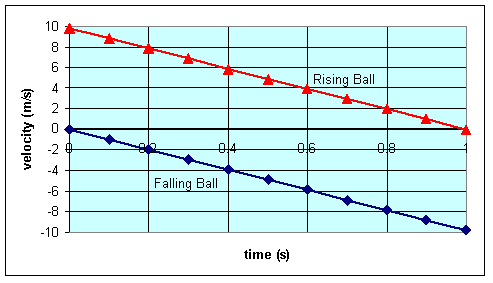
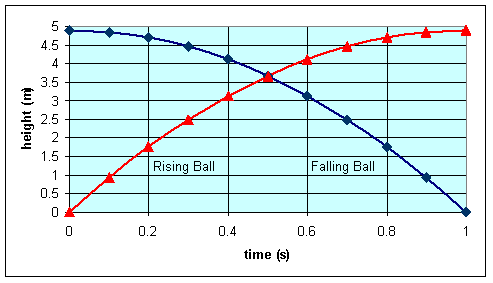
Assume the ball falls for 1 second. The speed of the falling ball as a
function of time is v = 9.8 (m/s2) t and the distance traveled is d = ½ 9.8 (m/s2) t2. In one second the ball travels 4.9 m. The velocity of the falling ball as a function of time is
v = -9.8 (m/s2) t j and its position as a
function of time is r = (4.9 m - ½ 9.8 (m/s2) t2) j.
The velocity of the rising ball as a function of time is
v = (9.8 (m/s) - 9.8 (m/s2) t) j and its position as a function of time is
r = (9.8 (m/s) t - ½ 9.8( m/s2) t2) j. Graphs of
velocity and position vs. time for the two balls are shown below.
Problem:
A stone is thrown directly upward with an initial speed of 4 m/s
from a height of 20 m. After what time interval does the stone strike the ground?
Solution:
- Reasoning:
We have motion in one dimension with constant acceleration. Put the
origin of your coordinate system at the position of the stone at t = 0 and
let the x-axis point straight downward. Then we know that
xi = 0, vxi
= -4 m/s, ti
= 0,
xf = 20 m, vxf = ?, tf
= ?,
ax = 9.8 m/s2.
We are asked to solve for t = tf.
- Details of the calculation:
We have xf
- xi = vxi∆t + ½ax∆t2,
20 m = -4 (m/s) t + 4.9 (m/s2) t2.
We rewrite this equation as t2 - (4
s/4.9) t - (20 s2/4.9)
= 0, or t2 - (0.816 s)t - 4.08 s2 = 0.
This is a quadratic equation with two solutions.
t = (0.816 s)/2 ± sqrt[((0.816 s)/2)2 + 4.08) = 0.408 s ±
2.061 s
Only the + sign makes sense. We find t = 2.47 s
Problem:
What is the speed of the stone in the previous problem when it hits the
ground?
Solution:
- Reasoning:
There are different ways to find the answer. One way is to use the
equation vxf2 = vxi2
+ 2ax(xf - xi).
All the quantities on the right-hand side are known, we can solve for vxf.
- Details of the calculation:
Here (xf - xi) = 20 m, ax = 9.8 m/s2,
and vxi = -4m/s.
Therefore vxf2 = (16 + 2*9.8*20)(m/s)2, vxf
= 20.2 m/s.
Note: If the stone is thrown directly downward with an initial speed
of 4 m/s, it hits the ground with the same speed, but at a later time.
When the stone thrown upward returns to its original
position, its velocity is -vi.
The magnitude is that of the initial velocity, but the sign of the
velocity has changed.
The velocity is now in the downward direction.
From then on, the stone behaves exactly like a stone throw downward
with the same initial speed.
Problem:
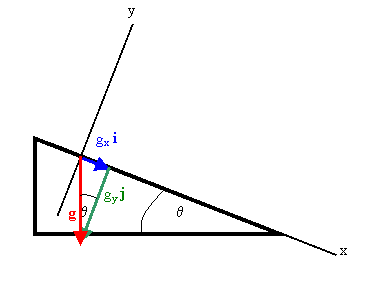Galileo experimented with balls rolling down inclined planes, in order to
reduce the acceleration along the plane and thus reduce the rate of descent
of the balls. Suppose the angle that the inclined plane makes with the
horizontal is θ. How would you expect the acceleration along the plane
to decrease as θ decreases. What specific trigonometric dependence on
θ would you expect for the acceleration?
Solution:
- Reasoning:
Acceleration is a vector. The gravitational acceleration
vector g is pointing straight down. Vectors can be written in terms
of their components along the axes of a coordinate system. If we choose our
coordinate system as shown, then the x-component of g is parallel and
the y-component of g is perpendicular to the surface of the inclined
plane.
We have gx = g sinθ. The object is constrained to
move on the surface of the plane, and therefore will accelerate in the
x-direction. We expect the magnitude of the acceleration to be
equal to gx and to depend on θ as sinθ .
Problem:
A pebble is dropped into a water well, and the splash is heard 16 s
later. What is the approximate distance from the rim of the well to
the water's surface?
Solution:
- Reasoning:
If we assume that the pebble is a freely falling object, then
the distance covered by the pebble in time t is d = ½gt2,
where g = 9.8 m/s2 is the gravitational acceleration. If the
pebble were falling for 16 s, the d = ½9.8 (m/s2) 256 s2
= 1254 m and its speed at that time would be v = gt = 9.8 (m/s2)
16 s = 156 m/s = 351 mph. However, since the speed of sound is 343 m/s, we
would only hear the splash after 19.6 s. The pebble must therefore be
falling for a shorter time and travel a shorter distance. It must fall for
somewhere between 13 s and 14 s. Let us assume it falls for 13.5 s. Then d
= 893 m. Sound covers this distance in 2.6 s. So 890 m is roughly right,
as long as we are justified to neglect air resistance.
Problem:
A hard rubber ball, released at chest height, falls to the pavement and
bounces back to nearly the same height. When it is in contact with the
pavement, the lower side of the ball is temporarily flattened. Assume that
the maximum depth of the dent in the ball is about 1 cm. Make an order of
magnitude estimate of the maximum acceleration of the ball. State your
assumptions, the quantities you estimate, and the values you estimate for them.
Solution:
- Reasoning:
The ball falls from chest height, so it falls for a
distance of approximately 1.3 m under constant acceleration g. It
falls for a time
t = (2d/g)½ and contacts the ground with speed v = gt .
The center of the ball
now moves another centimeter before the ball stops and v = 0.
- Details of the calculation:
The ball falls for a time
t = (2d/g)½ = 0.51 s
and contacts the ground with speed v = gt = 5 m/s.
The center of the ball
now moves another centimeter before the ball stops and v = 0.
We can
use vxf2 - vxi2 = 2ax(xf
- xi) to find the average acceleration of the ball during
this time interval.
-(5 m/s)2 = 2 ax 0.01 m. ax
= -1205 m/s2.
Problem:
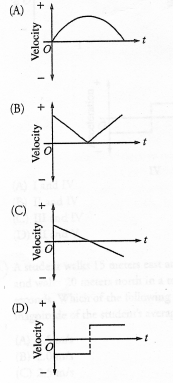A ball rolls up an incline, and then rolls back down to its initial position.
Which of the following graphs best represents the velocity of the ball as a
function of time?
Solution:
- Reasoning:
If we orient the x-axis of our coordinate system so it
points uphill along the incline, then at t = 0 vx is positive.
The velocity vx decreases linearly since ax points
into the negative x-direction. When the ball reaches its highest point, vx
= 0, when it rolls back down the incline vx is negative. The
graph (C) best represents the velocity of the ball as a function of time.
Module 2: Question 2
An object is dropped from a roof of a building of height h. During the
last second of its descent, it drops a distance h/3. Calculate the height
of the building.
Discuss approaches to solving this problem with your fellow students in the discussion forum!
